Метод прогонки для краевых задач

Краевые задачи для обыкновенного дифференциального уравнения 2-го порядка

Постановка задачи. На отрезке [a, b] требуется найти решение уравнения , удовлетворяющее краевым условиям

.

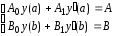Пример: .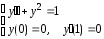

Вопрос о разрешимости краевой задачи не имеет универсального ответа не только в общем случае, но даже для линейных уравнений.

Пример:

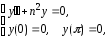
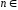N.

Эта задача имеет для каждого фиксированного 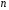два решения: y=0 и y=sin nx. Можно привести пример краевой задачи для линейного уравнения, не имеющей решения.

Вопрос о разрешимости краевой задачи для нелинейного дифференциального уравнения открыт до сих пор. Для линейных дифференциальных уравнений этот вопрос решен:

1) однородная задача

имеет не более конечного числа линейно-независимых решений;

2) неоднородная задача

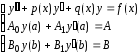
разрешима тогда и только тогда, когда f(x), A, B удовлетворяют конечному числу условий ортогональности.

В дальнейшем будем предполагать, что решение краевой задачи существует и единственно.

Существует несколько способов решения краевых задач. Рассмотрим конечно-разностный или сеточный способ.

Разобьем промежуток [a; b] на n частей узловыми точками x_i=a+ih, где 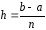– шаг вычислений, y_i=y(x_i). Построим конечно-разностную аппроксимацию неоднородной задачи:

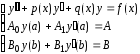. (1.9)

с краевыми условиями:

;

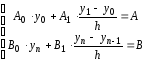. (1.10)

Введем обозначения b₀=A₀·h-A₁, c₀=A₁, d₀=Ah, a_n=-B₁, b_n=B₀·h +B₁, d_n=Bh, тогда уравнения запишутся:

b₀y₀+c₀y₁=d₀ ;

a_ny_n-1+b_ny_n=d_n .

Для основного уравнения применим аппроксимацию

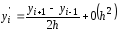; ; тогда пренебрегая слагаемыми второго порядка при подстановке в уравнение, получим:

.

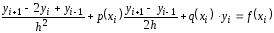Будем считать, что p_i=p(x_i), q_i=q(x_i), f_i=f(x_i), тогда получим:

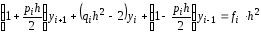, обозначим

, , , .

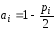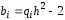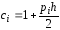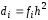Разностная аппроксимация для основного уравнения запишется так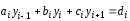. Индекс i меняется от 0 до n, но при i=0 не определено i-1, а при i=n не определено i+1, значит, основное уравнение имеет смысл только при i=1,2,3…, n-1. Таким образом, получено n-1 уравнение, вместе с двумя уравнениями аппроксимации краевых условий получится система из n+1 уравнения, содержащая n+1 неизвестное: y₀,y₁…, y_n. Решив эту систему, можно найти приближенные значения функции y=y(x) в узловых точках, т.е. получить сеточное решение краевой задачи (1.9)-(1.10).

Системы линейных алгебраических уравнений решают разными способами: по правилу Крамера, матричным методом через обратную матрицу, разложением матрицы на произведение двух треугольных, но самым рациональным является метод Гаусса, он требует наименьшего объема вычислений. Система, которую требуется решить, особенная – в каждом уравнении не более трех переменных. Для таких систем в 50-х гг. прошлого века советские математики предложили упрощенную схему метода Гаусса – метод прогонки.

Запишем всю систему уравнений

b₀y₀+c₀y₁ =d₀;

a₁y₀+b₁y₁+c₁y₂ =d₁;

a₂y₁+b₂y₂+c₂y₃= d₂;

. . .

a_n-1y_n-2+b_n-1y_n-1+c_n-1y_n=d_n-1;

a_ny_n-1+by_n =d_n.

Матрица такой системы состоит в основном из нулей, ненулевые элементы расположены только на главной диагонали и на двух линиях вдоль нее:

b₀ c₀ . . . . . . . .

a₁ b₁ c₁ . . . . . .

. a₂ b₂ c₂ . . . . . . . .

. . . . . . . .

.. . . a_n-1 b_n-1 c_n-1

. . . . . . a_n b_n

Такие матрицы называются ленточными, или трехдиагональными. Именно для систем с такими матрицами и разработан метод прогонки. Как и метод Гаусса, он состоит из двух этапов – прямого хода и обратного хода.

Прямой ход. Из первого уравнения выразим y₀ :

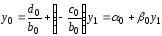, где ; .

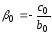Подставим это выражение y₀ во второе уравнение:

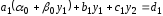, теперь оно содержит две неизвестных, выразим y₁

,

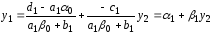где ; .

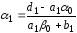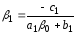Подставим выражение для y₁ в следующее уравнение:

и выразим из него y₂

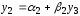, где ; .

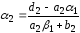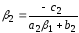Таким образом, можно выразить :

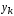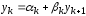, где ; .

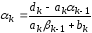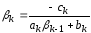Продолжим вычислять значения 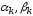пока не дойдем до последнего уравнения: 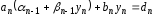, в этом уравнении всего одна неизвестная, найдем ее значение: .

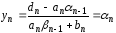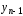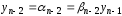Обратный ход. Зная y_n, можно найти . Зная , можно найти . С каждым шагом узнаем значение новой переменной, номер которой на 1 меньше предыдущей. Так добираемся до y₀. Все переменные найдены, задача решена.

Метод прогонки решения краевых задач является методом второго порядка точности. Основное достоинство метода – устойчивость. При оценке погрешности следует применять правило двойного пересчета Рунге.