Пособие ТОКН

Федеральное агентство по образованию Дальневосточный государственный технический университет (ДВПИ им. В.В. Куйбышева)

А.Н. Жирабок, В.Е. Небогатых

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ КОНСТРУИРОВАНИЯ И НАДЕЖНОСТИ

ЭЛЕКТРОННЫХ СРЕДСТВ

Издательство

ДВГТУ

Владивосток • 2008

УДК 621.396 Ж 73

Рецензенты:

В.Ф. Филаретов, д-р техн. наук, профессор, зав. лабораторией ИАПУ ДВО РАН; Н.В. Сгребнев, канд. техн. наук, зав. каф. электронной схемотехники и микропроцессоров

МГУ им. Г.И. Невельского

Жирабок, А.Н.

Ж 73 Теоретические основы конструирования и надежности электронных средств: учеб. пособие / А.Н. Жирабок, В.Е. Небогатых; Дальневосточный государственный технический университет. – Владивосток: Изд-во ДВГТУ, 2008. – 136 с.

ISBN 978-5-7596-1024-3

Систематически излагаются методы теории планирования эксперимента для построения моделей технических систем, основы теорий точности и надежности. Рассматриваются способы построения линейных и квадратичных планов и методы анализа построенных моделей; способы учета производственных погрешностей, а также дестабилизирующих факторов на примере температуры и старения; методы расчета и повышения показателей надежности.

Пособие предназначено для студентов вузов специальностей «Проектирование и технология радиоэлектронных средств», «Управление и информатика в технических системах», «Информационные системы и технологии».

УДК 621.396

ISBN 978-5-7596-1024-3	© Дальневосточный государственный
	технический университет, 2008

ВВЕДЕНИЕ

Разнообразные технические системы проникли практически во все сферы человеческой деятельности, без них невозможно представить современную жизнь. Это вынуждает обращать самое пристальное внимание на качественные показатели функционирования таких систем, их надежность, безопасность, отказоустойчивость. Последнее привело к возникновению ряда новых научных дисциплин – теории надежности, технической диагностики, теории живучести, гарантоспособности. Каждая из них решает свою задачу, внося определенный вклад в повышение эффективности технической системы.

Вопросы конструирования и технологии производства электронных средств имеют большое значение для создания современных радиоэлектронных комплексов и систем, качество которых в значительной мере зависит от выбранных схемных, конструкторских и технологических решений при их разработке и производстве. Поиск оптимальных решений опытным путем практически невозможен; здесь необходимо использовать теоретические подходы, базирующиеся на математических моделях рассматриваемых объектов и явлений и математических методах оптимизации. От конструк- тора-технолога электронных средств требуется умение строить такие модели на основе системного подхода, анализировать их и делать обоснованные выводы.

Изучение дисциплины «Теоретические основы конструирования и надежности электронных средств» является одним из этапов подготовки специалистов конструкторов-технологов электронных средств. Целью дисциплины является изучение теоретических предпосылок и математического аппарата для построения моделей и оптимизации конструкций и технологических процессов производства электронных средств, а также для проведения точностных и надежностных расчетов при их проектировании.

Особое внимание уделяется системному подходу при анализе и описании конструкций электронных средств и технологических процессов. Это необходимо для учета всех факторов, влияющих на конструкцию или технологический процесс, с целью построения моделей, адекватных рассматриваемому объекту.

Учебное пособие состоит из трех разделов. В первом рассматривается задача построения математических моделей электронных средств и их элементов, что необходимо для решения задач, возникающих при их проектировании. Одним из наиболее эффективных инструментов построения моделей является теория планирования эксперимента, которая позволяет не только оптимальным образом спланировать эксперимент, но и с наибольшим эффектом обработать его результаты. Теория планирования эксперимента, изучаемая в работе, позволяет строить формальные модели, которые описывают объект полиномами. В процессе решения задач, связанных с построением моделей

3

и их анализом, возникает ряд вопросов, рассматриваемых в традиционных курсах математической статистики, некоторые понятия которой также внесены в первый раздел.

Второй раздел посвящен изложению точностных расчетов – важнейших при проектировании электронных средств различного назначения, поскольку обоснованное назначение допусков на параметры элементов и правильный выбор их номинальных значений оказывает существенное влияние на главные характеристики проектируемых электронных средств: их тактико-технические данные, срок службы, стоимость. Рассматриваются задачи анализа и синтеза допусков, а также сопутствующие им вопросы.

В третьем разделе изучаются основы теории надежности как одной из многочисленных научных дисциплин, появившихся вскоре после Второй мировой войны, которая дала мощный толчок развитию различных отраслей техники, так или иначе связанных с военными приложениями. Излагаются основные понятия теории, методы расчета показателей надежности, а также методы повышения надежности как аппаратных, так и программных средств.

1. МЕТОДЫ ПОСТРОЕНИЯ МОДЕЛЕЙ

Задача построения моделей технических систем и процессов является необходимым этапом при изучении этих объектов с целью дальнейшего управления ими. Одним из наиболее эффективных инструментов построения моделей является теория планирования эксперимента, которая позволяет не только оптимальным образом спланировать эксперимент, но и с наибольшим эффектом обработать его результаты. Теория планирования эксперимента в рассматриваемом ниже виде позволяет строить так называемые формальные модели, которые описывают объект полиномами. Их называют формальными из-за того, что нередко отдельные члены этих полиномов не имеют физического смысла. Общий вид такого полинома – линейный, квадратичный или более высокой степени – определяется исходя из решаемой задачи; в итоге требуется определить коэффициенты, с которыми отдельные слагаемые входят в полином.

В процессе решения задач, связанных с построением моделей и их анализом, возникает ряд вопросов, изучаемых в традиционных курсах математической статистики, некоторые понятия которой целесообразно рассмотреть перед изложением непосредственно теории планирования эксперимента.

1.1.Элементы математической статистики

1.1.1.Оценки и требования к ним

Поскольку при проведении эксперимента на интересующий нас объект действуют различные возмущающие факторы, а измерения сопровождаются погрешностями, коэффициенты описывающего объект полинома не могут быть определены абсолютно точно. В связи с этим возникает понятие оценки как приближенного значения коэффициента, найденной по результатам эксперимента. Принято обозначать оценку коэффициента α символом αˆ .

Во многих случаях может быть несколько вариантов определения оценки некоторого коэффициента, в связи с чем возникает задача выбора наилучшего варианта, удовлетворяющего ряду требований. Приведем некоторые требования, отметив предварительно, что в связи с наличием указанных возмущений и погрешностей оценки являются случайными величинами.

1. Несмещенность. Формально записывается в виде M[αˆ ] = α – среднее значение оценки должно совпадать с точным значением коэффициента. Это означает, что оценка не имеет систематической ошибки.

2. Эффективность. Формально записывается в виде D[αˆ ] → min – из множества оценок необходимо выбрать ту, которая имеет наименьшую дисперсию. Это означает требование максимальной точности оценки.

3. Рекуррентность. Формально записывается в виде αˆ n+1 = f (αˆ n , хn+1) и

означает, что оценка αˆ n+1 при наличии n +1 измерений должна определяться на основе оценки, найденной по результатам n измерений и последнего измере-

5

ния хn+1. Требование рекуррентности очень важно для обработки поступаю-

щих измерений в реальном масштабе времени. Например, обычная (нерекуррентная) формула для подсчета оценки по результатам прямых независимых

равноточных измерений –

это среднее αˆ n

=

1

n

∑xi. Преобразуем ее к рекур-

рентному виду для n + 1 измерений:

n i=1

1

n+1

1

n

1

n

1

αˆ n+1 =

∑xi =

( ∑xi + xn+1) =

(n αˆ n + xn+1) =

αˆ n +

xn+1.

n +1

n +1

n +1

n +1

n +1 i=1

i=1

Таким образом, при наличии рекуррентной формулы отпадает необходимость в обработке все увеличивающегося числа измерений, что делается в нерекуррентном случае.

Необходимо отметить, что требования несмещенности и эффективности не всегда сочетаются; так, несмещенная оценка может не быть эффективной, и наоборот. В частности, такую особенность имеет оценка дисперсии (см., напри-

мер, формулы (1.2), (1.10) и (1.11)).

1.1.2. Методы получения оценок 1. Одним из наиболее популярных является метод наименьших квадра-

тов (МНК); рассмотрим его на примере решения следующей задачи. Для некоторого объекта с одним входом x и выходом y требуется построить модель, т.е. приближенное описание зависимости между переменными x и y. Зададим n значений переменной x – x1, x2 ,..., xn и произведем n измерений величины y –

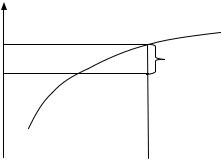
y1, y2 ,..., yn . Каждая пара измерений (xi , yi ) , i = 1, 2, …, n, дает точку на координатной плоскости (рис. 1.1).

y

•

yi*

yi

•

•

•

x xi

Рис. 1.1. Иллюстрация к методу наименьших квадратов

По виду расположения точек или из физических соображений назначается вид модели, т.е. функция f (x,α,β,...) – линейная, экспоненциальная, синусои-

6

дальная и т.д. В эту модель входит ряд коэффициентов (параметров) α,β,..., оценки которых и определяются рассматриваемым методом. Для этого в каждой точке составляются разности между измеренным значением величины yi и

ее значением yi*, предсказанным с помощью функции f:

e	= y	i	− y* = y	i	− f (x	,α,β,...) ,	i = 1, 2, … , n.
i			i		i

Эти разности можно интерпретировать как результаты действия возмущений на объект и погрешностей измерений. Далее составляется сумма квадратов всех этих разностей и минимизируется за счет выбора значений параметров:

n

e = ∑( yi − f (xi ,α,β,…))2 → min . i=1

Если функция f (x,α,β,...) дифференцируема, то это делается стандартным образом – взятием частных производных по параметрам α,β,..., приравниванием их 0 и решением полученной системы уравнений.

Если, например, функция f (x,α,β,...) линейна, т.е. y = αx + β, то в резуль-

тате проведенных операций получаем следующие выражения для оценок:

αˆ = ∑∑

yi (xi − x)	,	ˆ	(1.1)
(x − x)2		β = y − αˆ ,
i

где x = n1 ∑xi , y = 1n ∑yi (пределы суммирования для простоты опущены).

В заключение отметим, что метод наименьших квадратов дает эффективные оценки.

2. В основе метода максимального правдоподобия лежит интуитивно яс-

ная идея: из ряда случайных событий скорее всего реализуется то, которое имеет наибольшую вероятность.

Рассмотрим следующую задачу: имеется некоторый объект, который описывается переменной x и коэффициентами (параметрами) α,β,...; проведенный над объектом эксперимент дал серию значений этой переменной: x1, x2 ,..., xn . Требуется определить оценки параметров α,β,.... Для решения задачи составляется так называемая функция правдоподобия L, по смыслу равная вероятности получения величин x1, x2 ,..., xn , и максимизируется за счет выбора значений

параметров.

Рассмотрим конкретный пример: имеется несимметричная монета, для определения степени асимметрии которой подбрасываем ее n раз, в результате чего

7

орел выпал m раз. Оценим степень асимметрии монеты вероятностью p выпадения орла при одном бросании. Тогда вероятность полученного рассматриваемого события – «m выпадений орла при n бросаниях» – определяется выражением

P = L = Cnm pm (1 − p)n−m ,

которое и является искомой функцией правдоподобия. Найдем значение p, при котором это выражение принимает максимальное значение, для чего (в целях упрощения расчетов) перейдем к логарифму величины L:

L* = ln L → max,		L* = ln Cnm + m ln p + (n − m) ln(1 − p),
∂L*	= m	− n − m	= 0, m(1 − p) = p(n − m),
∂p	p	1 − p

откудаследует p = m / n, что иследовалоожидатьисходяизздравыхсоображений.

3. В случае, когда параметры, оценки которых требуется определить, входят в выражение для плотности вероятности некоторой случайной величины,

используется метод моментов.

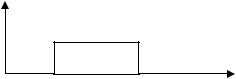
Рассмотрим его на примере следующей задачи. Имеется случайная величина X, распределенная по равномерному закону с параметрами α и β (рис. 1.2),

αβ

Рис. 1.2. Равномерный закон распределения

и в эксперименте получено n реализаций этой величины: x1, x2 ,..., xn . Метод моментов для

этой задачи состоит в том, что рассчитываются

xдва теоретических момента – математическое ожидание и дисперсия, и два статистических – оценки этих моментов. Соответствующие формулы имеют следующий вид:

	М[ X ] =	α +β	,	D[X ] =	(β − α)2
		2			12

для теоретических моментов и

ˆ	1	∑xi ,	ˆ	1		∑(xi − x)	2
M[X ] = x =	n		D[X ] =	n −1				(1.2)

для статистических моментов.

8

Приравнивая эти моменты, получаем систему уравнений

	α + β	=	1		∑xi ,
	2		n
	(β − α)2					1
								∑(xi − x)	2
				=						,
	12					n −1

решая которую, определяем оценки параметров α и β.

Если функция плотности вероятности содержит только один параметр (что выполняется, например, для экспоненциального закона распределения, когда ϕ(x) = λexp(−λx) , x ≥ 0 ), используется только один из моментов – математиче-

ское ожидание или дисперсия; выбирается тот из них, который лучше описывает рассматриваемую задачу.

1.1.3. Статистическая проверка гипотез В научных и инженерных приложениях нередко встречается ситуация, ко-

гда приходится принимать одно из возможных решений, опираясь при этом на не вполне достоверную информацию, что неизбежно приводит к риску принятия неверных решений. Полезно рассмотреть эту ситуацию в общем виде на простейшем примере двух возможных решений, что известно в математической статистике как статистическая проверка гипотез.

Пусть имеется некоторое явление, относительно которого можно выдвинуть две гипотезы: H0 – основную (наиболее предпочтительную), H1 – альтер-

нативную. Для принятия решения о том, какая гипотеза верна, проводится эксперимент, результаты которого представлены семейством чисел x1, x2 ,..., xn .

Назначается критерий r = f (x1, x2 ,..., xn ) – результат обработки полученных

чисел. Пусть М – множество всех возможных значений критерия. Назначается достаточно малая вероятность α ( α = 0,01÷0,05), называемая уровнем значимости, которая определяет так называемую критическую область K М , удовлетворяющую следующему условию:

P(r K / H0 ) ≤ α.

Приведенное выражение означает, что если верна основная гипотеза H0 ,

то вероятность того, что значение критерия r принадлежит критической области, не превосходит α – весьма малой величины. Отсюда ясно, что если r K , то принимается гипотеза H1, если r K , то принимается гипотеза H0 , точнее,

делается заключение о том, что полученные данные не противоречат гипотезе H0 ; иногда выражаются более жестко – гипотезу H0 нельзя отвергнуть.

9

Из сказанного следует, что α представляет собой вероятность ошибочного решения – принять гипотезу H1, когда она неверна. Возможно и другое оши-

бочное решение – принять гипотезу H0 , когда она неверна. Ясно, что жела-

тельно уменьшить вероятности обеих ошибок, но, как правило, уменьшение одной из них приводит к увеличению другой.

1.2.Теории планирования эксперимента. Основные понятия

Вподразд. 1.3-1.7 рассматриваются основы теории планирования эксперимента, которая находит широкое применение при решении различных задач, возникающих в процессе проектирования и производства электронных средств. Одной из главных является задача построения математической модели изучаемого процесса или объекта. Обычно модель ищется в виде полинома подходящей степени; ясно, что чем выше степень полинома, тем точнее модель. С другой стороны, для построения сложного полинома требуется весьма сложный эксперимент, а результаты такого эксперимента с трудом поддаются интерпретации. В таких случаях приходится принимать компромиссное решение. Обычно оно заключается в том, что строится линейная либо квадратичная модель. Эти модели хорошо интерпретируются, и эксперименты для их построения сравнительно просты.

Также весьма важными являются задачи оптимизации, например поиск таких условий проведения сложного технологического процесса, при которых его выходной параметр достигает своего максимального или минимального значения. Эти задачи также могут быть решены методами теории планирования эксперимента.

Вкачестве простого примера, когда планирование при проведении даже простого эксперимента позволяет повысить эффективность получаемых результатов, рассмотрим популярную задачу о взвешивании трех предметов А, В и С на весах. Традиционный подход состоит в том, что вначале взвешивается пустая чашка, на которую затем по очереди кладутся предметы и определяется вес каждого из них вместе с чашкой. План такого эксперимента приведен в табл. 1.1, где

знаками «+» и «–» отмечено наличие и отсутствие предмета на чашке соответственно. Ясно, что вес предмета А определяется следующим образом: VA =V2 −V1.

Таблица 1.1

План традиционного эксперимента

	А	В	С	Вес
1	–	–	–	V1
2	+	–	–	V2
3	–	+	–	V3
4	–	–	+	V4

10