двойные интегралы

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ

Методические указания по проведению практических занятий для студентов технических специальностей

Владивосток 2013

УДК 517.37

ББК 22.1

Вычисление двойных интегралов.: метод. Указания / Сост.

Н.Е. Дегтярева. – Владивосток: Изд-во ДВФУ, 2013. – 27с.

В краткой форме излагается основной теоретический материал, входящий в раздел векторного анализа «кратные интегралы и их приложение». Содержит 10 вариантов заданий для самостоятельной работы студентов: примеры по построению областей интегрирования, замены пределов интегрирования и переменных при переходе в полярную систему координат.

Приведены решения типовых заданий и список дополнительных задач.

Методические указания предназначены для студентов технических специальностей.

Методические указания печатаются с оригинал-макета,

подготовленного автором

©Н.Е.Дегтярева

©Изд.-во ДВФУ, 2013

2

f (x, y)

1. Двойной интеграл в декартовой системе координат

Двойным интегралом от непрерывной функции f (x, y),

распространенным на ограниченную замкнутую область S плоскости xOy,

называется предел существующей двумерной интегральной суммы:

f (x, y)dxdy

lim f (xi, yk ) xi yk

(1.1)

Smax xi 0 i k max yk 0

где xi xi 1 xi , yk yk 1 yk и сумма распространена на те значения i и k, для которых точка (xi, yk ) принадлежит области S.

Замечание: произведение дифференциалов аргументов dxdy функции есть не что иное, как некоторый элемент площади рассматриваемой

области S, поэтому данное произведение можно записывать как ds.

При расстановке пределов различают два основных вида области

интегрирования:
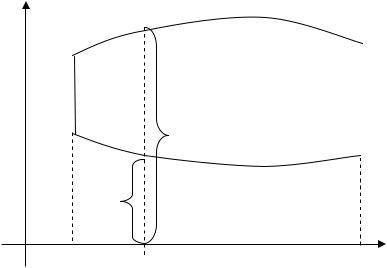
1)	Область	S	ограничена слева и справа прямыми x a и					x b
(b a),	а снизу	и	сверху	непрерывными кривыми			y (x) (AB) и
y (x) (CD),		каждая из		которых пересекается		с	вертикальюx X
(a X b) только в одной точке (рис.1.1).
	y				y (x)
		D					C
		A			y2		B
			y1		y (x)		x
	O		a	X	Рис. 1.1	b

В заданной области S переменная x изменяется в интервале от a до

b, а переменная y, при постоянном значении x, изменяется от (x) до

3

(x). Вычисление двойного интеграла производится путем сведения его к повторному интегралу по формуле:

					b	(x)
			f (x, y)dxdy dx f (x, y)dy						(1.2)
		S			a	(x)
			(x)
где при вычислении			f (x, y)dy величину x полагают постоянной.
			(x)
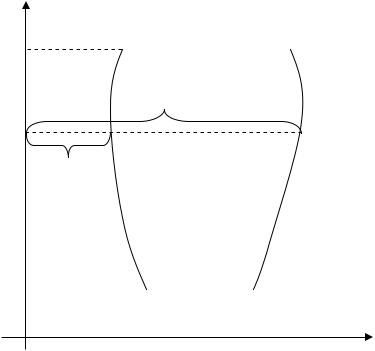
2)	Область	S	снизу и сверху ограничена прямыми y c и						y d
(d c),	а слева	и справа			непрерывными кривыми			x (y)(AB) и
x (y) (CD),		каждая из			которых	пересекается с		вертикалью	y Y
(c Y d) только в одной точке (рис.1.2).
	y		B			C
	d
					x2

Y

x1

S

x (y)

x (y)

с

A D

x

O	Рис.1.2

По аналогии с предыдущим получим повторный интеграл вида:

	d	(y)
f (x, y)dxdy dy f (x, y)dx			(1.3)
S	c	(y)
	(y)
В котором интеграл	f (x, y)dx вычисляется в предположении, что
	(y)

переменная y постоянна.

4

Свойства двойного интеграла применяемые при вычислениях:

1)Линейности:

f (x, y) g(x, y) dxdy

S

f (x, y)dxdy g(x, y)dxdy.

S S

2)Аддитивности:

f (x, y)dxdy		f (x, y)dxdy ... f (x, y)dxdy;
S	S1	Sk
Если S S1	... Sk

2.Практикум

1.Для указанного повторного интеграла записать уравнения линий ограничивающих область и вычертить эту область.

4	3 x				6	2 y			3			2 x
1) dx f (x, y)dy,					2) dy f (x, y)dx,				3) dx			f (x, y)dy;
2 x2					1 y2				1 x2
				1				1					2
	3					4						5
4	9 y				3	5 x			2	y
4) dy f (x, y)dx,					5) dx f (x, y)dy,				6) dy f (x, y)dx;
0		y			3	x			1	1
			1				2
	3					2				y
2		1 x			2		1 y		3 3 x2
7) dx			f (x, y)dy,		8) dy			f (x, y)dx,	9) dx f (x, y)dy;
3	x2 3				2	y2 2			1	x 2

4 10 y

10)dy f (x, y)dx.

0y

2.Для указанной треугольной области D расставить пределы интегрирования в повторном интеграле, в том и в другом порядке:

1)	A(1;1), B(0; 3), C(1; 2),	2)	A(2; 0), B(2; 4), C(5; 3);
3)	A(0; 0), B(3; 2), C(3;1),	4)	A( 1;1), B(3;1), C( 2; 2);
5)	A(2;1), B(2; 3), C(0; 0),	6)	A( 2; 1), B(3; 2), C(4; 1);

5

7)	A(1; 3), B(1; 2), C( 2;1),	8) A(3;1), B( 1;1), C(0; 2);
9)	A( 3;1), B( 3; 4), C(2; 3),	10) A( 1; 2), B(3; 2), C(1; 2).

3.Вычислить интеграл.

	2	x 1		1	2x
1)	dx (3x 2y2)dy,		2)	dx (x2 3y)dy;
	0	0		1	0
	2	3x		4	3x
3)	dx (2x 3y2)dy,		4)	dx (x2 y)dy;
	1	1		0	1
	5	4x		3	1 x
5)	dx (x 4y2)dy,		6)	dx (2x2 y)dy;
	0	1		1	0
	4	3x		2	4 x
7)	dx (y2 5x)dy,		8)	dx (4y x2)dy;
	0	0		2	3
	0	1 x		3	5
9)	dx (y2 x)dy,		10) dx (y 5x2)dy.
	2	2		0	x 4

3.Решение типового варианта

1.Для указанного повторного интеграла записать уравнения линий

5

7 x

ограничивающих область и вычертить эту область dx

f (x, y)dy.

3

x2

1

6

5

x1 3,

Решение:

Для

переменной

x

из интеграла

dx

имеем:

3

x2 5. Для

y

7 x

переменной

из

интеграла

f (x, y)dy

получаем

x

2

1

6

аналогично: y

x2

1, y

2

7 x.

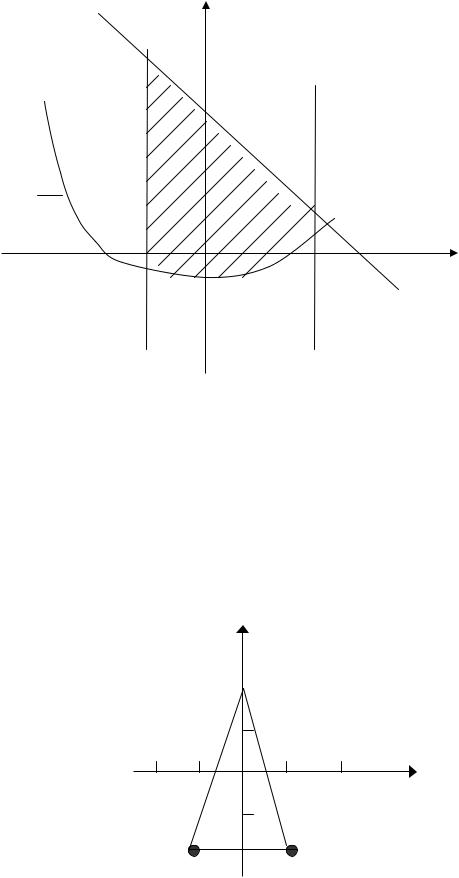
Строим указанные линии на графике

1

6

(рис.3.1) и заштриховываем полученную область.

6

y

7

y 7 x

y x2 1 16

	O	7	x
x 3	-1	x 5

Рис. 3.1
2. Для указанной треугольной области S: A(1; 2),	B(0; 2),
C( 1; 2) расставить пределы интегрирования в повторном интеграле, в
том и в другом порядке.
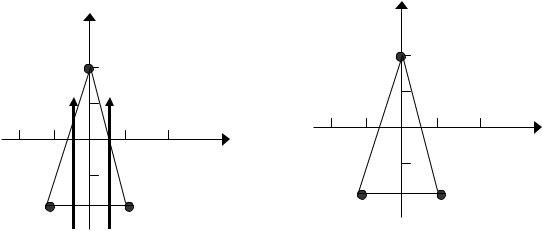
Решение: По точкам строим указанную область (рис.3.2)
Наш интеграл можно представить повторным в виде: dy	f (x, y)dx
или dx f (x, y)dy.

y

B

x

O

C A

Рис.3.2

7

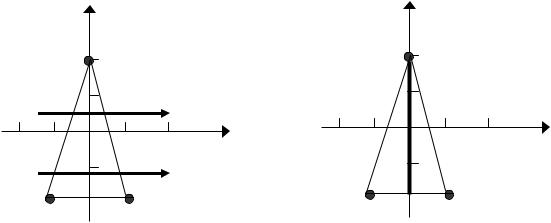
1) Расставим	пределы интегрирования в повторном интеграле	вида
dy f (x, y)dx.	Внутренним является интеграл по переменной	x:

f (x, y)dx. Значит, проведем через нашу область S стрелки параллельно оси Ox (рис.3.3). Из рисунка видим, что они вошли в прямую (СB) и,

пройдя область S, вышли из прямой (AB).

	y		y
	B		B
	x		x
	O		O
C	A	C	A
	Рис. 3.3		Рис.3.4

Запишем уравнения этих прямых, используя формулу уравнения

прямой проходящей через две точки:

x x1

y y1

.

x2 x1

y2 y1

Прямая

(CB)

запишется

в

виде

x 1

y 2

. Выразим из

0 1

2 2

полученного

уравнения переменную

x:

x

y 2

.

Аналогично прямая

4

(AB):

x 1

y 2

. Выражаем

x:x

2 y

.

Таким образом, переменная

2 2

0 1

4

величина x будет изменяться от x

y 2

до x

2

2 y

.

1

4

4

Переменная y будет меняться в пределах проекции области S на ось

Oy (рис.3.4): от пересечения оси Oy прямой AC ( y1 2) до координаты ординаты точки B( y2 2).

Проставим полученные пределы в повторном интеграле:

8

	2	2 y
		4
	dy f (x, y)dx.
	2	y 2
		4
2) Расставим	пределы	интегрирования в повторном интеграле вида
dx f (x, y)dy.	Внутренним является интеграл по переменной y:

f (x, y)dy. Значит, проведем через нашу область D стрелки параллельно оси Oy (рис.3.5).

y			y
B			B
		x	x
O			O
		S1	S2
C	A	C	A
Рис. 3.5		Рис.3.6

Из рисунка видим: обе стрелки входят в прямую (CA), а выходят из

разных прямых: одна из прямой (CB), другая - из (AB). В таком случае,

согласно свойству аддитивности, область интегрирования разбивается на две:

S1 и S2 (рис.3.6), а наш интеграл распишется на сумму двух интегралов, по

каждой из областей: f (x, y)dxdy f (x, y)dxdy.

S1 S2

Для расстановки пределов интегрирования запишем уравнение прямой

(CA): y 2 (т.к. прямая параллельна оси Ox). Выразим из уравнений прямых (СB) и (AB) (построены в предыдущем пункте) переменную y.

Для прямой (CB): y 4x 2, для прямой (AB): y 2 4x.

9

	По области S1	переменная		y меняется от уравнения прямой (CA):
y1 2 до уравнения прямой (СB): y2 4x 2. Переменная						x от точки
пересечения прямых (CA)и(СB)				C : x1 1 до оси Oy: x2	0.
	По области S2	переменная		y меняется от y1 2 до	y2	2 4x, а
переменная x от оси Oy: x1 0 до абсциссы точки A: x2 1.
	Запишем полученный интеграл:
0	4x 2	1	2 4x
dx	f (x, y)dy dx		f (x, y)dy.
1	2	0	2

Данный пример показывает, как важно правильно выбрать порядок интегрирования в повторном интеграле. Или вычисляем только один интеграл, или два.

4	3x 5
3. Вычислить повторный интеграл dx		(3x2		2y)dy
1		1
		2x

Решение: Вычислим первый интеграл по переменной y полагая, что x- константа.

3x 5

3x 5

3x 5

3x 5

y

2

3x 5

(3x2 2y)dy 3x2

dy 2

ydy 3x2 y

2

.

1

1

1

1

2

1

2x

2x

2x

2x

2x

По формуле Ньютона-Лейбница подставляем вместо переменной y

верхний и нижний пределы:

			2						1					2	1			2
		3x			(3x 5						)		(3x 5)		(		)
																2x
									2x
	3			2			63		1
9x		6x						x				25.
							2
										4x2

Полученное выражение подставляем в следующий интеграл:

4	3		2		63		1
(9x		6x				x		25)dx;
1					2		4x2

10