Женщина / Пример_Флетчер_ривс

Этот метод относится к группе методов сопряженных направлений, при которых шаги итерационной процедуры минимизации целевой функции предпринимаются в сопряженных направлениях. Два n-мерных вектора x и y называют сопряженными по отношению к матрице H (или H-сопряженными), если скалярное произведение (x,Hy)=0. Здесь H – симметричная положительно определенная матрица размером n x n [11].

Методы сопряженных направлений обладают по сравнению с градиентными методами более высокой скоростью сходимости. Минимум положительно определенной квадратичной функции n переменных

(49)

может быть найден не более чем за n шагов из любой начальной точки, если эти шаги предпринимать в сопряженных направлениях. Любая гладкая функция в окрестности точки минимума хорошо аппроксимируется квадратичной, поэтому методы сопряженных направлений успешно применяются для минимизации также не квадратичных функций. В таком случае методы перестают быть конечными и становятся итеративными.

Наиболее существенна при методах сопряженных направлений проблема эффективного построения таких направлений. Метод Флетчера - Ривса решает эту проблему путем преобразования на каждом шаге антиградиента - в направлении , H – сопряженном с ранее найденными направлениями . Рассмотрим сначала этот метод применительно к задаче минимизации квадратичной функции (49).

Направление вычисляются по формулам:

,

(50)

Величины выбираются так, чтобы направления были H-сопряженными: (51)

В результате для квадратичной функции:

(52)

Итерационный процесс минимизации имеет вид

, где (53)

- называют величиной шага, а n-мерный вектор - направлением спуска на k-том шаге. Величина шага выбирается из условий минимума функции в направлении движения:

(54)

Для квадратичной функции (55)

Алгоритм сопряженных градиентов состоит в следующем:

1. В точке вычисляется ;

2. На k-ом шаге по формулам (55) и (53) определяется шаг и точка ;

3. Вычисляются величины и ;

4. Если , то точка является минимумом функции. В противном случае из соотношения:

(56)

определяется новое направление и осуществляется переход к следующей итерации. Благодаря этой процедуре минимум квадратичной функции находится не более чем за n шагов. При минимизации не квадратичных функций метод Флетчера -Ривса из конечного становится итеративным. В таком случае после итерации шаги 1 – 4 алгоритма повторяются с заменой на , а вычисления заканчиваются при , где - заданная точность.

Пример 9. Найти минимум функции . Начальная точка (9; -7; 11) [2] .

Решение: Итерационный процесс приведен в таблице 4.

Таблица 4.

№ итерации	x1	x2	x3	F
1	9	-7	11	418
2	-0,481	0,111	7,83	37,14
3	1,206	2,827	4,862	4,965
4	0,999	2	3	4,26E-14

Оптимальное значение найдено на 4 шаге.

Пример №1. Найти минимум функции методом сопряженных градиентов: f(X) = 2x₁²+2x₂²+2x₁x₂+20x₁+10x₂+10. Решение. В качестве направления поиска выберем вектор градиент в текущей точке:

▽ f(X) =

4*x1+2*x2+20 2*x1+4*x2+10

Итерация №0.

▽ f(X₀) =

20 10

Проверим критерий остановки: |▽f(X₀)| < ε Вычислим значение функции в начальной точке f(X₀) = 10. Сделаем шаг вдоль направления антиградиента.

X₁ = X₀ - t₀▽ f(X₀) =

0 0

- t₀

20 10

=

-20.0*t0 -10.0*t0

f(X₁) = 2*(-20.0*t₀)²+2*(-10.0*t₀)²+2*(-20.0*t₀)*(-10.0*t₀)+20*(-20.0*t₀)+10*(-10.0*t₀)+10 → min Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f '(x₁)=0): 2800*t₁-500 = 0 Получим шаг: t₀ = 0.1786 Выполнение этого шага приведет в точку:

X₀ =

0 0

- 0.1786

20 10

=

-3.5714 -1.7857

Итерация №1.

▽ f(X₁) =

2.143 -4.286

Проверим критерий остановки: |▽f(X₁)| < ε Вычислим значение функции в новой точке f(X₁) = -34.643. X² = X¹ - t₁d₁ d₁ = ▽f(X¹) + b₀▽f(X⁰)

d₁ =

2.143 -4.286

+ 0.0459

20 10

=

3.061 -3.827

Сделаем шаг вдоль направления антиградиента.

X₂ = X₁ - t₁▽ f(X₁) =

-3.5714 -1.7857

- t₁

3.061 -3.827

=

-3.0612*t1-3.5714 3.8265*t1-1.7857

f(X₂) = 2*(-3.0612*t₁-3.5714)²+2*(3.8265*t₁-1.7857)²+2*(-3.0612*t₁-3.5714)*(3.8265*t₁-1.7857)+20*(-3.0612*t₁-3.5714)+10*(3.8265*t₁-1.7857)+10 → min Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f '(x₂)=0): 49.198250728863*t₂-22.9591836734694 = 0 Получим шаг: t₀ = 0.4667 Выполнение этого шага приведет в точку:

X₀ =

-3.5714 -1.7857

- 0.4667

3.061 -3.827

=

-5 0

Итерация №2.

▽ f(X₂) =

0 0

Проверим критерий остановки: |▽f(X₂)| < ε Вычислим значение функции в новой точке f(X₂) = -40.

Анализ решения. Найдем матрицу Гессе функции f(X) = 2x₁²+2x₂²+2x₁x₂+20x₁+10x₂+10.

H =

4	2
2	4

Так как матрица Гессе является положительно определенной, то функция f(X) строго выпукла и, следовательно, в стационарной точке достигает глобальный минимум.

1. Все переменные выражаются через x₁,x₂

2. Все математические операции выражаются через общепринятые символы (+,-,*,/,^). Например, x₁²+x₁x₂, записываем как x1^2+x1*x2.

Дважды непрерывно дифференцируемая функция f(x) является выпуклой (вогнутой) тогда и только тогда, когда матрица Гессе функции f(x) по x положительно (отрицательно) полуопределена для всех x (см. точки локальных экстремумов функции многих переменных).

Критерии определенности матрицы (теорема Сильвестра). Положительная определенность:

• все диагональные элементы матрицы должны быть положительны;

• все ведущие главные определители должны быть положительны.

Положительная полуопределенность:

• все диагональные элементы неотрицательны;

• все главные определители неотрицательны.

Главный определитель – это определитель главного минора.

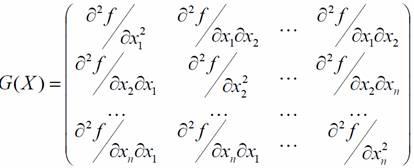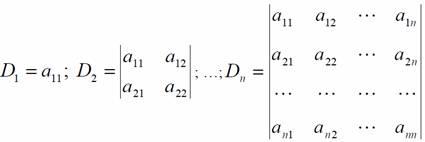Квадратная симметрическая матрица порядка n, элементами которой являются частные производные целевой функции второго порядка, называется матрицей Гессе и обозначается: Для того, чтобы симметрическая матрица была положительно определена, необходимо и достаточно, чтобы все ее диагональные миноры были положительны, т.е. для матрицы A= (a_ij) положительные. Для того чтобы симметрическая матрица была отрицательно определена, необходимо и достаточно, чтобы имели место неравенства: (-1)^k D_k> 0, k =1,.., n.

Примечание. Чтобы найти обратный гессиан достаточно найти обратную матрицу.