Вступ

Методичні вказівки та індивідуальні завдання з курсу вищої математики за темами „Лінійна та векторна алгебра” та „Аналітична геометрія на площині та у просторі” складено відповідно до програми курсу.

Мета розробки: перевірка знань студентів з основних понять і методів курсу, прищеплення у студентів навичок самостійної роботи.

Типові розрахунки можуть бути використані викладачами для контролю знань студентів, для проведення аудиторних індивідуальних практичних занять, а також як домашні індивідуальні завдання.

Розділ 1. Лінійна алгебра

1.1 Матриці та дії над ними

Поняття матриці та відповідний розділ математики мають важливе значення для економістів, оскільки велика кількість досліджувальних об’єктів і процесів досить просто, а головне – компактно, подається в матричній формі.

Матрицеюрозміруназивається множина зелементів, розміщених у вигляді прямокутної таблиці зрядків істовпців:

	(1.1)
,	(1.2)

де – елемент матриці;– номер рядка;– номер стовпця.

Матриці бувають різних типів: прямокутні, квадратні, діагональні, одиничні, нульові та інші.

Квадратною матрицеюназивається матриця, в якій кількість рядків і стовпців однакова. Їх кількість вказує розмір матриці.Головною діагоналлюквадратної матриці називається діагональ, яка проходить через верхній лівий та нижній правий кути матриці, тобто сукупність елементів.

Квадратну матрицю, в якій всі елементи, окрім тих, що розташовані на головній діагоналі, дорівнюють нулю, називають діагональною матрицею.

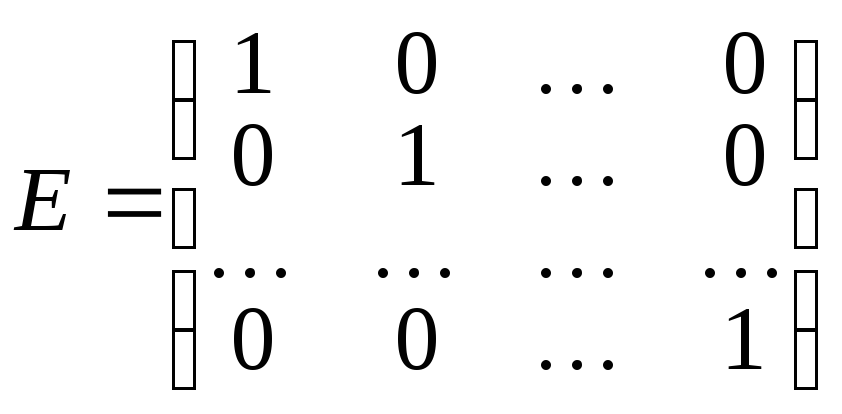
Діагональну матрицю, в якій всі елементи дорівнюють одиниці, називають одиничноюі позначають літерою.

.

(1.3)

Матриця називається трикутною, якщо всі її елементи під (над) діагоналлю дорівнюють нулю.

Нульовою матрицеюназивається матриця, всі елементи якої дорівнюють нулю.

Над матрицями, як і над числами, можна виконувати різні операції, причому деякі з них – аналогічні операціям над числами, а деякі – специфічні.

Розрізняють наступні дії над матрицями:

1. Операція порівняння: дві матрицітаназиваються рівними, якщо рівні їх відповідні елементи, тобто.

2. Множення матриці на число:добутком матриціна числоназивається матриця, елементи якої визначаються за формулою

.

(1.4)

3. Додавання та віднімання матриць:сумою двох матрицьіназивається матриця, елементи якої визначаються за формулою

.

(1.5)

Додавати можна матриці лише однакового розміру, тобто матриці з однаковою кількістю рядків і стовпців.

Властивості операцій додавання та віднімання матриць:

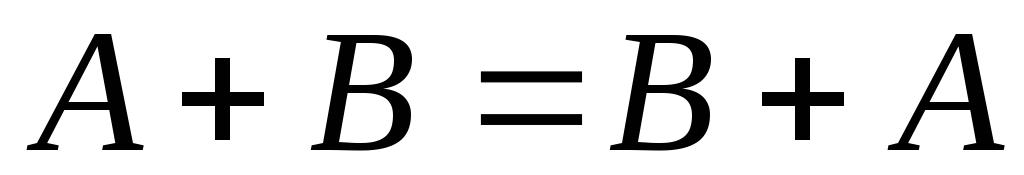• (комутативність);

• (асоціативність);

• (дистрибутивність);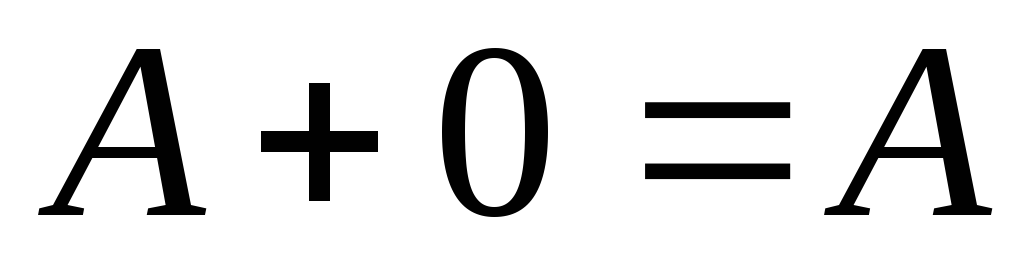

• (нейтральність нульової матриці).

4. Транспонування матриці:транспонованою матрицею до матриціназивається така матриця, в якій рядки та стовпці міняються місцями, і позначається літерою.

5. Множення матриць: добутком двох матриць іназивається матриця, елементи якої визначаються за формулою

.

(1.6)

Перемножать можливо лише такі дві матриці, в яких кількість стовпців першої збігається з кількістю рядків другої:

.

(1.7)

Добутком двох матриць є матриця, в якій кількість рядків дорівнює кількості рядків першої матриці, а кількість стовпців – кількості стовпців другої матриці.

Властивості добутку матриць:

• ;

• ;

• ;

• ;

• ;

• .

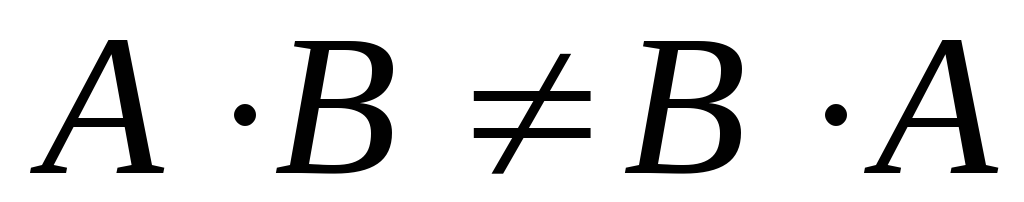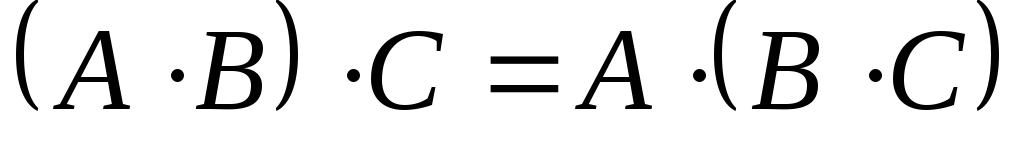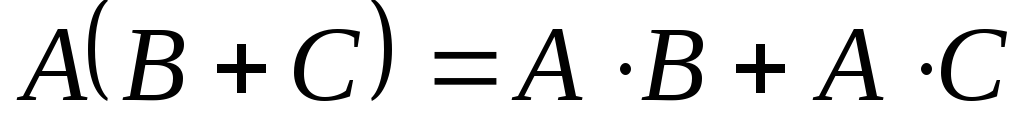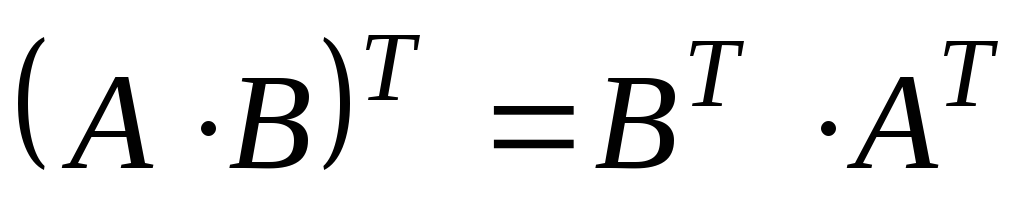1.2 Означення та основні властивості визначників

Квадратній матриці можна поставити у відповідність число, що обчислюється за певним правилом і називається визначником. Його позначають символомабо. Правило, за яким обчислюється визначник, залежить від порядку матриці.

Визначник другого порядкуобчислюється наступним чином:

.

(1.8)

Визначник другого порядку дорівнює різниці добутків елементів головної та побічної діагоналі.

Визначником третього порядку називається число, що обчислюється за таким правилом:

.

(1.9)

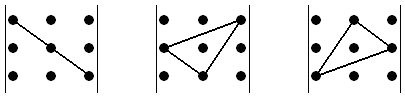
Формула (1.9) – це формула „трикутника” для обчислення визначника третього порядку. Якщо елементи матриці третього порядку позначити точками, то три доданки, що беруться зі знаком „+”, лежать на головній діагоналі й у вершинах трикутників, одна із сторін яких паралельна головній діагоналі (рис.1.1).

Рис.1.1

Аналогічні співмножники від’ємних доданків лежать на побічній діагоналі й у вершинах трикутників, одна із сторін яких паралельна їй (рис.1.2).

Рис.1.2

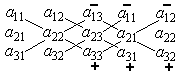
За іншою схемою дописують два перші стовпці до матриці, внаслідок чого одержують прямокутну матрицю розміром . Тоді додатні та від’ємні доданки формули (1.9) беруть за схемою (правило Саррюса), зображеною на рис.1.3.

Рис.1.3

Міноромелементавизначника називається визначник меншого на одиницю порядку, отриманий із даного шляхом викреслення з нього-го рядка та-го стовпця.

Алгебраїчним доповненням елементавизначника називається величина, яку знаходять за формулою

.

(1.10)

Визначникдорівнює сумі добутків будь-якого рядка чи стовпця на їхні алгебраїчні доповнення.

Властивості визначників:

• значення визначника не зміниться при його транспонуванні (тобто замінити рядки стовпцями і навпаки);

• якщо всі елементи деякого рядка чи стовпця визначника дорівнюють нулю, то і сам визначник дорівнює нулю;

• якщо у визначнику поміняти місцями два сусідні рядки чи стовпці, то знаки таких визначників будуть протилежними, а їх абсолютні значення – однаковими;

• визначник із двома однаковими рядками чи стовпцями дорівнює нулю;

• якщо деякий рядок чи стовпець визначника помножити на довільне число , то значення визначника зміниться уразів;

• значення визначника не зміниться, якщо до будь-якого рядка додати інший, помножений на довільне число або лінійну комбінацію інших рядків;

• сума добутків усіх елементів деякого рядка або стовпця на алгебраїчні доповнення до іншого рядка або стовпця визначника дорівнює нулю;

• якщо елементи будь-якого ряду визначника можна подати у вигляді суми, то цей визначник можна подати у вигляді деяких визначників;

• сума добутків елементів будь-якого ряду визначника на алгебраїчні доповнення, які відповідають елементам іншого паралельного ряду, дорівнює нулю.

У матричному численні важливу роль відіграває поняття оберненої матриці.

Матриця , яка задовольняє співвідношення

(1.11)

називається оберненоюдо матриціі позначається.

Для того, щоб квадратна матриця мала обернену матрицю, необхідно і достатньо, щоб її визначник не дорівнював нулю. Обернену матрицю можна знайти різними способами. Один із них полягає у побудові приєднаної матриці. Транспонована матриця, яка складена із алгебраїчних доповнень до їх елементів, називаєтьсяприєднаною і позначається:

.

(1.12)

Тоді обернену матрицю можливо знайти наступним чином:

.

(1.13)
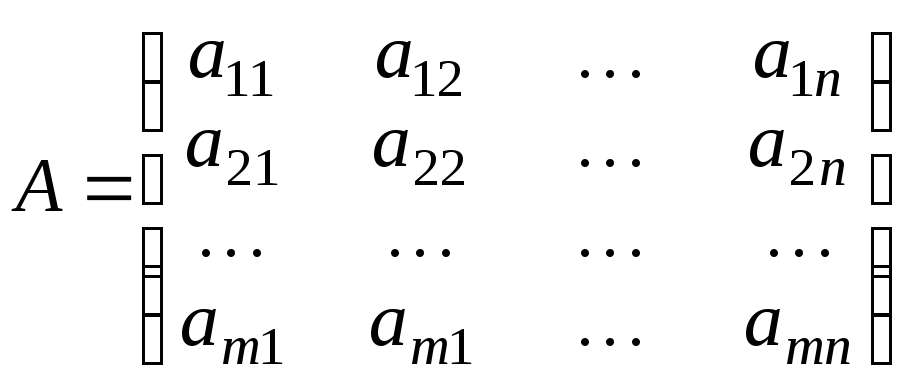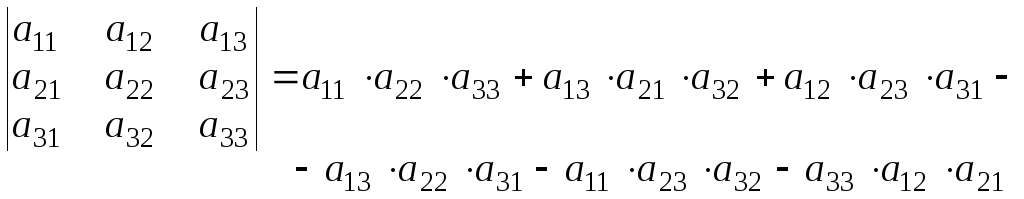
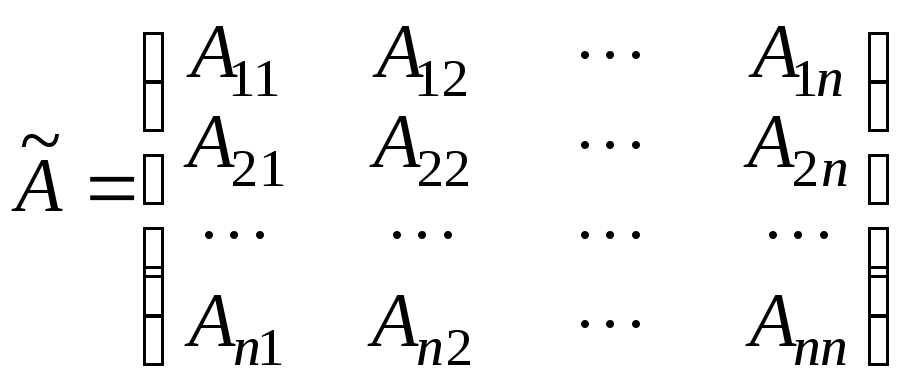