1. Границя послідовності

1.1. Числова послідовність

Визначення. Якщо кожному натуральному числу n поставлено у відповідність число х_n, то говорять, що задано послідовність

x_1, х₂, …, х_n = {x_n}.

Загальний елемент послідовності є функцією від n, тобто x_n = f(n).

У такий спосіб послідовність може розглядатися як функція порядкового номера елемента.

Задати послідовність можна різними способами – головне, щоб був зазначений спосіб одержання будь-якого члена послідовності.

Приклад. {x_n} = {(-1)ⁿ} або {x_n} = -1; 1; -1; 1; …

{x_n} = {sinn/2} або {x_n} = 1; 0; 1; 0; …

Для послідовностей можна визначити наступні операції:

1. Множення послідовності на число m: m{x_n} = {mx_n}, тобто

mx₁, mx₂, …

2. Додавання (віднімання) послідовностей: {x_n}  {y_n} = {x_n  y_n}.

3. Добуток послідовностей: {x_n}{y_n} = {x_ny_n}.

4. Частка послідовностей: 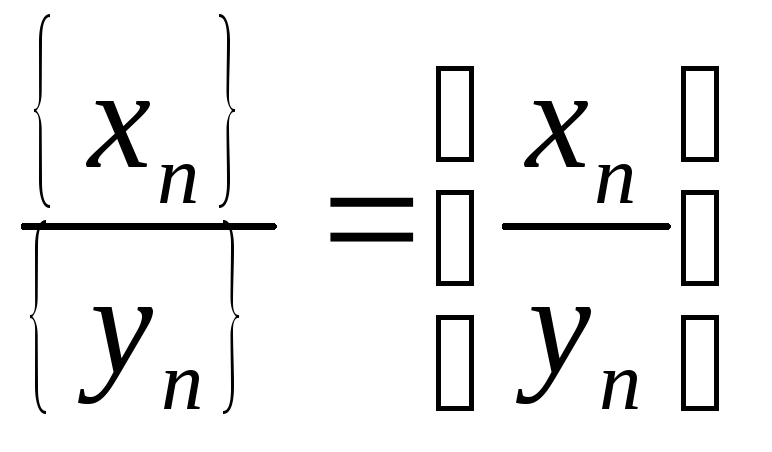при {y_n}  0.

1.2. Обмежені й необмежені послідовності

Визначення. Послідовність {x_n} називається обмеженою, якщо існує таке число М>0, що для будь-якого n вірна нерівність:

,

тобто всі члени послідовності належать проміжку (-М; M).

Визначення. Послідовність {x_n} називається обмеженою зверху, якщо для будь-якого n існує таке число М, що

x_n  M.

Визначення. Послідовність {x_n} називається обмеженою знизу, якщо для будь-якого n існує таке число М, що

x_n  M.

Приклад. {x_n} = n – обмежена знизу {1, 2, 3, … }...

Теорема. Послідовність не може мати більше однієї границі.

Теорема. Якщо x_n  a, то .

Теорема. Якщо x_n  a, то послідовність {x_n} обмежена.

1.3. Монотонні послідовності

Визначення. 1) Якщо x_n+1 > x_n для всіх n, то послідовність зростаюча.

2) Якщо x_n+1  x_n для всіх n, то послідовність не убуваюча.

3) Якщо x_n+1 < x_n для всіх n, то послідовність убуваюча.

4) Якщо x_n+1  x_n для всіх n, то послідовність не зростаюча.

Всі ці послідовності називаються монотонними. Зростаючі та убуваючі послідовності називаються строго монотонними.

Приклад. {x_n} = 1/n – убуваюча й обмежена;

{x_n} = n – зростаюча й необмежена.

Приклад. Довести, що послідовність {x_n}=монотонна зростаюча.

Знайдемо член послідовності {x_n+1}= .

Знайдемо знак різниці: {x_n}-{x_n+1}=

, тому що nN, то знаменник позитивний при будь-якому n.

Таким чином, x_n+1 > x_n. Послідовність зростаюча, що й треба було довести.

Приклад. З'ясувати – це зростаюча або убуваюча послідовність

{x_n} = .

Знайдемо . Знайдемо різницю

, тому що nN, то 1 – 4n <0, тобто х_n+1 < x_n. Послідовність монотонно спадає.

Слід зазначити, що монотонні послідовності обмежені принаймні з однієї сторони.

Теорема. Монотонна обмежена послідовність має границю.

Приклад . 2, 4, 6, … , 2, … – це є монотонна необмежена послідовність.

Приклад. 1, 0, 1, 0, … – не монотонна й необмежена.

Визначення. Число А називається границею послідовності , якщо для будь-якого як завгодно малого невід’ємного числа існує номертакий, що всі значенняв якихзадовольняють нерівності

. (1.1)

Записують або а_n  А при .

Приклад

,…– не монотонна обмежена.

Можна помітити, що члени послідовності з ростом, як завгодно близько наближаються до 1. При цьому абсолютна величина границі різницістає все менше й менше:

, ,, …,,…

Рис. 1.1

Тобто при зростанні величинабуде менша за будь-яке як завгодно мале невід’ємне число.

Нехай, наприклад, Тоді із (1.1) маємо:; а якщо підставити, то. Аналогічно для. Нерівність (1.1) виконується для. Отже для, що виконується нерівність (1.1):, а це значить, щоабо.

Маємо геометричну інтерпретацію границі числової послідовності:

Рис. 1.2

Для будь-якого знайдеться номер, починаючи з якого усі члени послідовності будуть замкнені в– околиці точки А.