1. Лабораторная работа №6Минимизация логических функций

2. Цель работы

• Освоить понятия минимизации логических функций (ЛФ).

• Научиться мимнимизировать ЛФ методом Квайна-Мак-Класски.

• Научиться мимнимизировать ЛФ с помощью карт Карно.

3. Теоретические сведения

Определение. Минимальная форма (МКФ и МДФ) представления ФЛ это форма, которая содержит минимальное количество термов и переменных в термах, и не должна допускать последующих упрощений.

Например, функция x₁+x₂ может быть упрощена, если применить распределительный закон: x₁x₂+x₃=(x₁+x₃)(x₂+х₃), тогда

x₁+x₂=(+x₁)(x₁+х₂)=x₁+x₁x₁+х₂+x₁x₂=

=0+x₁+х₂(+x₁)=x₁+х_2.

Упрощение сложных логических выражений может быть осуществлено на основании применения законов и аксиом алгебры логики.

1. 6.1 Числовое и геометрическое представление фл

Многие преобразования, выполняемые над булевыми функциями, удобно интерпретировать с использованием их геометрических представлений f(x).

Так функцию двух переменных можно интерпретировать как некоторую плоскость, заданную в системе координат xy=x₁x₂. При произвольно выбранных единичных значениях x₁ и х₂ получается квадрат, вершины которого соответствуют комбинациям переменных (см. рисунок 6.1).

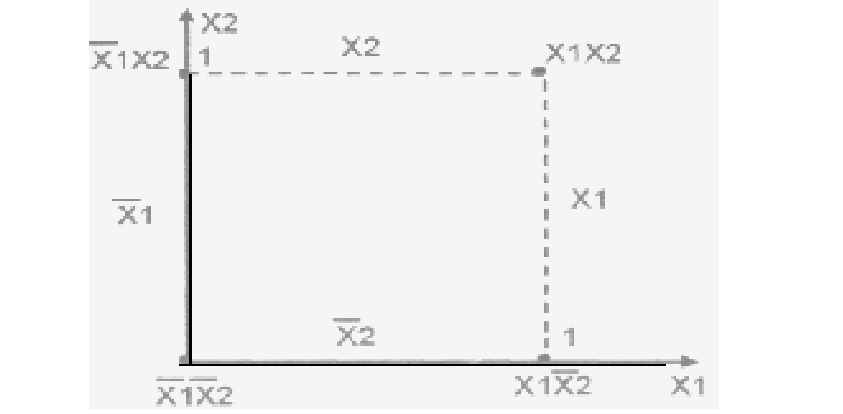
Рис. 6.1-Геометрическое представление ФЛ при n = 2.

Такое геометрическое представление функций двух переменных наглядно показывает: две вершины, принадлежащие одному ребру и называемые соседними, "склеиваются" по переменной, изменяющейся вдоль этого ребра.

Правило склеивания распространяется и на кубическое представление ФЛ.

На рисунке 6.2 показана область определения для произвольной функции трех переменных.

Элементам куба сопоставлены конъюнкции различного ранга: вершинам куба – третий ранг, ребрам куба - второй ранг, граням куба - первый ранг.

Определение. Сумма размерности геометрического эквивалента и ранга, сопоставляемая этому геометрическому эквиваленту конъюнкции, постоянна и равна числу аргументов функции.

Определение. Каждый геометрический эквивалент меньшей размерности покрывается всеми геометрическими эквивалентами большей размерности.

Рис. 6.2-Геометрическое представление ФЛ при n=3

По аналогии будем говорить о покрытии конъюнкции большего ранга соответствующими конъюнкциями меньшего ранга.

Например, конъюнкции x₁x₂x₃ и x₁x₂ покрываются конъюнкцией x₁x₂.

В общем виде операцию покрытия можно записать АВ+А=А. Чаще употребляется термин склеивание.

В геометрическом смысле каждый набор x_1,x₂,…,х_n может рассматриваться как n -мерный вектор, определяющий точку n-мерного пространства. Исходя из этого, множество наборов, на которых определена функция n переменных, представляют в виде вершин n-мерного куба.

Координаты вершин куба должны быть указаны в порядке, соответствующем порядку перечисления переменных в записи функций.

Отмечая точками вершины, в которых функция принимает значения, равные 1, получаем геометрическое представление ФЛ.

2. 6.2 Построение комплекса кубов и его минимального покрытия

Терм максимального ранга n- куба принято называть 0-кубом (точка вершины) и обозначают К⁰. Например, для f(x₁,x₂,x₃)= (0,4,7) комплекс 0-кубов будет таким

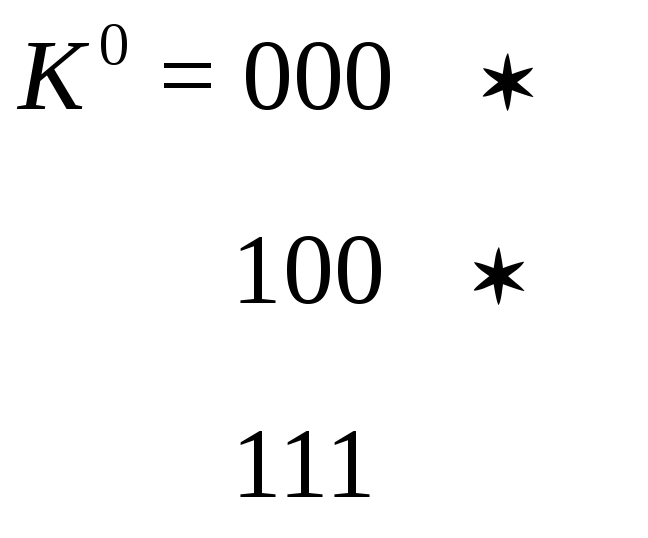
Определение. Если два 0-куба из комплекса К⁰ различаются только по одной координате, то два таких 0-куба образуют один 1-куб. Он представляется общими элементами 0-кубов, причем на месте координаты, по которой различаются 0-кубы, указывают символ Х, обозначающий независимую координату (переменную). Различие координат определяют последовательным сравнением первого куба с остальными, затем второго с остальными и так далее. Например, два 0-куба 000 и 100 различаются только по одной координате, и они образуют 1-куб (отрезок), которому соответствует ребро трехмерного куба. Заметим, что 0-куб 111 не склеивается, так как отличается больше чем по одной координате.

Все множество 1-кубов функции называется кубическим комплексом К- один и обозначается- К¹.

K¹ = {X00}

Комплекс К¹ строится по комплексу К⁰ путем их сравнения и определяет все множество ребер, на концах которых функция принимает единичные значения. Если два 1-куба из комплекса К¹ имеют общую независимую компоненту и различаются только по одной координате, то они образуют один 2-куб. Это грань для трехмерного куба. Все множество 2-кубов, построенного из комплекса К¹, образует множество комплекса К² (множество граней). Комплекс К³ = 0 - отсутствует в трехмерном кубе (часто r-куб называют интервалом (расстоянием) r- порядка). Перед построением очередного куба необходимо отметить те кубы, которые склеились хотя бы один раз. Например, звездочкой *. Это необходимо, так как могут быть неотмеченные (не склеившиеся) кубы о которых забывать нельзя. Они являются самостоятельными импликантами, которые так же включают в общее покрытие кубов С(f). Для нашего примера, общее покрытие будет выглядеть

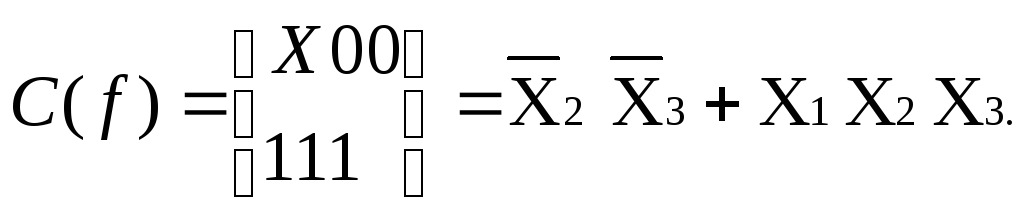
По индукции можно определить, что два r-куба, содержащие r координат и различающиеся только по одной координате, могут объединяться в (r + 1)-куб, (r + 1)-я независимая координата которого соответствует координате, по которой различаются r-кубы.

Запись (r + 1)-куба состоит из общих компонент двух r-кубов, а компонента, принимающая в них различные значения, обозначается в (r + 1)-кубе как независимая компонента Х.

Число независимых координат Х в кубе определяет его размерность.

Например, куб 0Х1Х1ХХ имеет размерность r = 4.

Определение. Объединение кубов комплексов К⁰,К¹,...,Кⁿ функции f(x₁, x₂, …, х_n) называется кубическим комплексом K(f) функции f.

K(f) = K(f) = К⁰ К¹ К² К³ ...

В отличие от аналитических форм записи булевых функций, кубическое представление позволяет задавать булевы функции в виде множества кубов, компонентами которых являются только три символа 0; 1; X. Ограниченное количество символов в записи функций алгебры логики позволяет автоматизировать процесс минимизации с применением компьютерных систем.

Задача минимизации булевых функций по критерию минимальности числа букв входящих в ДНФ или КНФ называется канонической задачей минимизации.

Схема, получаемая в результате ее решения не является абсолютно минимальной, т.к. абсолютный минимум оборудования в большинстве случаев так и не достигается.

Определение. Булева функция f(x₁, x₂, …, х_n) представляется как множество С кубов, принадлежащих комплексу К(f), и таких, что каждая вершина комплекса К⁰ включена по крайней мере в один куб множества С.

Полученное таким образом множество С называется покрытием комплекса K(f) и покрытием булевой функции. Каждому покрытию C(f) соответствует ДНФ функции.

Например, дана функция

f(х)= (3,4,5,6,7)= x₂x₃+x₁+ +x₁x₃+x₁x₂+x₁x₂x₃

Построим комплекс кубов К⁰,К¹,К²,К³.

К³= 0

Из комплекса кубов K(f) определяется его покрытие C(f) куда входят не отмеченная импликанта Х11 из куба К¹ и покрытие 1ХХ из куба К².

C(f) =

Это покрытие включает в себя все 5 вершин комплекса К°. В самом деле, куб x11 может включать (покрывать) 011; 111. Куб 1xx может включать вершины 100, 101, 110, 111. Таким образом, множество C(f) является покрытием комплекса K(f). Отсюда можно написать минимизированное уравнение:

f(х)= (3,4,5,6,7)=x₂x₃+x₁.