02_случайные величины / 02_закон распределения

§2. Закон распределения

Когда мы проводим наблюдения над случайной величиной, мы можем обнаружить, что одни возможные значения появляются чаще, другие реже. Т.е., у одних значений вероятность появления больше, у других меньше.

П

римеры:

Возьмем некоторые из примеров предыдущего параграфа.

1. Опыт – бросание кубика.

Случайная величина Х – выпавшее число очков.

Возможные значения {1, 2, 3, 4, 5, 6 }.

Вероятность появления любого из этих значений подсчитывается по классическому определению и равна (1/6). Все эти значения равновозможны, они появляются одинаково часто.

2. Опыт – лекция по теории вероятностей.

Случайная величина Х – число присутствующих студентов.

Возможные значения { 0, 1, 2, …, N }.

Пусть N = 50. Наблюдения преподавателя показывают, что достаточно часто на лекции присутствуют от 30 до 40 человек. Очень редко, но бывает, что на лекции присутствуют все 50 студентов. Значения 1, 2, 3 и т.д., в принципе возможны, но практически не наблюдались. Таким образом, в этом примере возможные значения случайной величины не равновозможны, вероятность появления у них разная.

3. Опыт – работа торгового предприятия в течение суток.

Случайная величина Х – суточная выручка.

Здесь тоже практические наблюдения показывают, что чаще всего сумма суточной выручки колеблется в определенных пределах, например 600-800 грн. Редко выпадают удачные дни, когда она составляет к примеру больше 2 тыс.грн. Также редко, но бывают, к сожалению и неудачные дни, когда выручка не превышает 100 грн. Совершенно очевидно, что некоторые из значений хотя и возможны, но практически не встречаются.

Так что и здесь возможные значения случайной величины имеют разную вероятность появления.

О3 : Законом распределения вероятностей случайной величины Х

( дальше везде будем говорить кратко – законом распределения ) называется всякое правило, устанавливающее соответствие между возможными значениями случайной величины и вероятностями того, что она примет эти значения.

Это соответствие можно устанавливать по-разному, в зависимости от того, с какой случайной величиной мы работаем, с дискретной или с непрерывной. Существуют три способа задания закона распределения, которые мы далее по очереди подробно рассмотрим.

Сейчас мы только перечислим их и отметим главное: если закон распределения задан (любым из этих способов) то мы можем прогнозировать поведение случайной величины. Точно предсказать до опыта, какое именно значение примет случайная величина, мы не можем в принципе, но зато мы сможем подсчитывать вероятность того, что она примет то или иное значение, попадет в интересующий нас интервал.

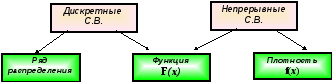
Способы задания закона распределения:

1. Ряд распределения;

2. Функция распределения F(x)

( иногда ее еще называют интегральная Функция распределения)

3. Плотность распределения f(x)

(ее еще называют также дифференциальная Функция распределения )

Следующая схема показывает,

когда применяется каждый из этих способов: