
§6. Числовые характеристики распределений
Закон распределения полностью определяет случайную величину и позволяет прогнозировать ее поведение. Если мы знаем закон распределения, то мы знаем о случайной величине все.
Но во многих случаях достаточно знать не весь закон распределения, а только несколько чисел, характеризующих этот закон. Это – числовые характеристики распределения.
Выделяют две основные группы таких чисел.
I. Характеристики положения:
-
Математическое ожидание случайной величины;
-
Мода;
-
Медиана.
II. Характеристики рассеивания (разброса):
-
Среднее абсолютное отклонение;
-
Дисперсия;
-
Среднеквадратическое (стандартное) отклонение.
Кроме того, рассматриваются также (хотя и намного реже)
-
Начальные и центральные моменты:
-
Асимметрия
-
Эксцесс.
Рассмотрим по очереди каждую из этих характеристик.

Характеристики положения.
-
Математическое ожидание случайной величины М[X], mx ;
Пусть задана дискретная случайная величина.:
|
x i |
2 |
5 |
8 |
|
p i |
0,7 |
0,2 |
0,1 |
Найдем среднее из всех возможных значений. Обычно в таких случаях суммируют все усредняемые значения и делят на их количество, т.е., вычисляют
среднее
арифметическое:
![]() .
.
Но эти значения не равноправны. Возможное значение 2 появляется в 7 раз чаще, чем значение 8. У них разная частота появления, разные вероятности, разный вес. И когда мы усредняем возможные значения, это обязательно нужно учитывать.
В математике для этого есть такое понятие как средневзвешенное. При таком усреднении каждое из значений умножается на его вес, на его долю, а затем все эти произведения складываются
2 • 0,7 + 5 • 0,2 +8 • 0,1 = 3,2.
Подсчитанное таким образом среднее значение случайной величины и называется математическим ожиданием.
Определение:
математическим
ожиданием
случайной
величины
называется
средневзвешенное
ее возможных значений.
Процесс усреднения проводится
следующим образом:
каждое
из возможных значений умножается на
его вероятность, и затем эти произведения
суммируются.
Расчетные формулы:
для дискретной случайной величины :
![]() ;
;
для непрерывной случайной величины :
![]() .
.

(
20 )
(
20 )
Для непрерывной случайной величины процедура усреднения производится точно так же: каждое возможное значение x умножается на его вероятность dP = f(x) • dx и потом производится суммирование по всем возможным значениям, в общем случае от (–) до (+). Только для дискретной случайной величины суммирование производится по отдельным точкам и поэтому стоит символ суммы , а для непрерывной случайной величины сумма превращается в интеграл.
Д ля
наглядности изобразим возможные значения
случайной величины на числовой оси (на
этот раз в масштабе) и кроме того, сами
точки тоже будут иметь масштаб,
соответствующий вероятности этих
значений.
ля
наглядности изобразим возможные значения
случайной величины на числовой оси (на
этот раз в масштабе) и кроме того, сами
точки тоже будут иметь масштаб,
соответствующий вероятности этих
значений.
Оказывается, что математическое ожидание находится в центре тяжести этой системы.
С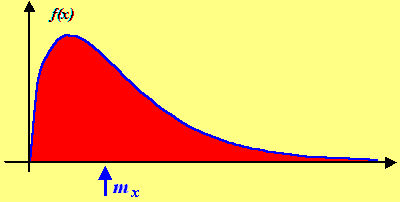 овершенно
аналогично, для непрерывной случайной
величины, которая задана плотностью
распределения,
математическое ожидание тоже связано
с положением центра тяжести.
овершенно
аналогично, для непрерывной случайной
величины, которая задана плотностью
распределения,
математическое ожидание тоже связано
с положением центра тяжести.
Точка на оси Ох, соответствующая центру тяжести графика плотности, это и есть математическое ожидание.
Замечание:
В теории
вероятности вообще, процесс осреднения
любых величин проводится точно так же,
как это делается для математического
ожидания.
Возможные
значения величины, которая усредняется,
умножаются
на вероятности этих значений,
и
затем эти произведения суммируются.

Свойства математического ожидания:
-
Математическое ожидание постоянной величины
M [C] = C.
(Если величина не случайная, то во всех опытах она принимает одно и то же значение, и поэтому среднее значение равно ей самой)
-
Постоянный сомножитель выносится за знак математического ожидания
M [ C · X ] = C · M [ X ] .
-
Математическое ожидание суммы
M [ X + Y ] = M [ X ] + M [ Y ].
(Равно сумме математических ожиданий).
-
Математическое ожидание произведения
M [ X · Y ] = M [ X ] · M [ Y ].
Последнее свойство применимо только для независимых случайных величин.
