Краткий конспект лекций

Матрицы и операции над ними.

Определение.Матрицей называется множество чисел, которое составляет прямоугольную таблицу, состоящее изmстрок иnстолбцов

коротко матрицу обозначают так:

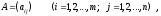
где элементы данной матрицы,i– номер строки,j– номер столбца.

Если в матрице число строк равно числу столбцов (m = n), то матрица называетсяквадратнойn-го порядка, а в противном случае –прямоугольной.

Если m=1 и n >1, то получаем однострочную матрицу

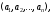
которая называется вектор-строкой, если, жеm>1 иn=1, то получаем одностолбцовую матрицу

,

которая называется вектор-столбцом.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой элементы главной диагонали равны единице, называется единично, обозначаетсяE.

Матрица, полученная из данной заменой ее строки столбцом с тем же номером, называется транспонированнойк данной. Обозначается.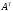

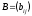Две матрицы иравны, если равны между собой элементы, стоящие на одинаковых местах, то есть если

при всех i иj(при этом число строк (столбцов) матрицAиBдолжно быть одинаковым).

1°. Суммой двух матрицA=(a_ij) иB=(b_ij) с одинаковым количествомm строк иnстолбцов называется матрицаC=(c_ij), элементы которой определяются равенством

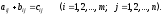
Сумму матриц обозначают C=A+B.

Пример.

.

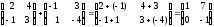2⁰. Произведением матрицыA=(a_ij) на числоλназывается матрица, у которой каждый элемент равен произведению соответствующего элемента матрицыAна числоλ:

λA=λ(a_ij)=(λa_ij), (i =1,2…,m ; j=1,2…,n ).

Пример.

3⁰. Произведением матрицыA=(a_ij), имеющейmстрок иkстолбцов, на матрицуB=(b_ij), имеющейk строк иnстолбцов, называется матрицаC=(c_ij), имеющаяmстрок иnстолбцов, у которой элементc_ijравен сумме произведений элементовi-ой строки матрицыA иj-го столбца матрицыB, то есть

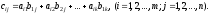
При этом число столбцов матрицы Aдолжно быть равно числу строк матрицыB. В противном случае произведение не определено. Произведение матриц обозначается A*B=C.

Пример.

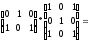
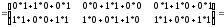
Для произведения матриц не выполняется равенство между матрицами A*B иB* A, в общем случае одна из них может быть не определена.

Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.

Пример.Пусть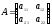,, тогда согласно правилу умножения матриц имеем

=

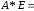
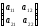
и

,

откуда заключаем, что

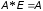и

Определители и их свойства.

Пусть дана квадратная матрица третьего порядка:

(1)

Определение. Определителем третьего порядка, соответствующим матрице (1), называется число, обозначаемое символом

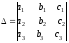
и определяемое равенством

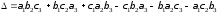.(2)

Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком "+", а какие со знаком "-", полезно использовать следующее правило треугольников.

+ -

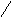
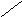
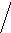
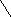
Пример.

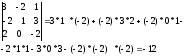
Сформулируем основные свойства для определителей третьего порядка, хотя они присущи определителям любого порядка.

1. Величина определителя не изменится, если его строки и столбцы поменять местами, т. е.

=

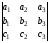
2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.

=-

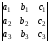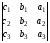
3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

4. Умножение всех элементов одного столбца или одной строки определителя на любое числоλравносильно умножению определителя на это число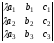λ.

= λ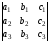

5. Если все элементы некоторого столбца или некоторой строки определителя равны нулю, то и сам определитель равен нулю.

6. Если элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

7. Если каждый элементn-го столбца (n-ой строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один вn-ом столбце (n-ой строке) содержит первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же.

Например,

=+

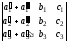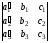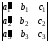
8⁰. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель, то величина определителя не изменится.

Например,

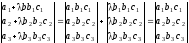
Миноромнекоторого элемента определителя называется определитель, получаемый из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Например, минором элемента а₁определителяΔявляется определитель 2-го порядка

.

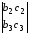Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на (-1)^p, гдер- сумма номеров строки и столбца, на пересечении которых расположен этот элемент.

Если, например, элемент а₂находятся на пересечении 1-го столбца и 2-ой строки, то для негор=1+2=3 и алгебраическим дополнением является

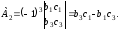
9⁰. Определитель равен сумме произведений элементов какого–либо столбца или строки на их алгебраические дополнения.

10⁰. Сумма произведений элементов какого–либо столбца или какой–либо строки определителя на алгебраические дополнения соответствующих элементов другого столбца или другой строки равны нулю.

Возникает вопрос, можно ли для квадратной матрицы А подобрать некоторую матрицу, такую что умножив на нее матрицу А в результате получить единичную матрицу Е, такую матрицу называют обратной к матрице А.

Определение. Матрица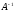называется обратной квадратной матрицеA, если.

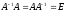Определение. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае квадратная матрица называется вырожденной.

Всякая невырожденная матрица имеет обратную.

Элементарными преобразованиями матрицявляются:

1. перестановка местами двух параллельных рядов матрицы;

2. умножение всех элементов матрицы на число, отличное от нуля;

3. прибавление ко всем элементами ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Матрица В, полученная из матрицыАс помощью элементарных преобразований, называетсяэквивалентнойматрицей.

Для невырожденной квадратной матрицы

третьего порядка обратная матрица А^-1может быть вычислена по следующей формуле

здесь Δ - определитель матрицы А,A_ij – алгебраические дополнения элементовa_ij матрицыА.

Элемент строки матрицы называется крайним, если он отличен от нуля, а все элементы строки, находящиеся левее него, равны нулю. Матрица называетсяступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки. Например:

- не ступенчатая; - ступенчатая.