Оулы 1-3

1.13	A1 2; 5;8 ,	A2 7; 3; 2 ,	A3 4;5; 7 ,	A4 4;2; 5 .
1.14	A1 8;5;3 ,	A2 5; 1;4 ,	A3 3;2; 1,	A4 4; 7;2 .

1.15A1 1;0;4 , A2 8;7; 8 , A3 3; 5;1 , A4 2;1;3 .

1.16A1 2;7;8 , A2 4; 3; 9 , A3 7;4; 3 , A4 4;9;7 .

1.17A1 8;0;9 , A2 4;3;5 , A3 2;1;7 , A4 4;6; 3 .

1.18A1 7;2;5 , A2 3; 8;4 , A3 5;3; 3 , A4 2;5; 4 .

1.19A1 2;1; 9 , A2 7;3;5 , A3 2;4; 7 , A4 6;4; 3 .

1.20A1 2; 8;1 , A2 8;7; 3 , A3 3;5; 8 , A4 7;0;2 .

1.21A1 7;5;9 , A2 4;8;6 , A3 7;2; 4 , A4 5;0;2 .

1.22A1 8; 5;3 , A2 7;2;1 , A3 4;3;2 , A4 8;7;4 .

1.23A1 3;0;5 , A2 4;7;2 , A3 4;5;3 , A4 2;1; 4 .

1.24A1 8; 7;3 , A2 4;0;5 , A3 2;3;7 , A4 4;5; 9 .

1.25A1 3;2; 1 , A2 4;7;0 , A3 5;3; 3 , A4 1;4;3 .

1.26A1 1;3; 7 , A2 2;1;8 , A3 6;1;0 , A4 3; 4;5 .

1.27A1 7; 4;0 , A2 3;5;2 , A3 4;7;5 , A4 2;1;9 .

1.28A1 4;0;7 , A2 8;6;4 , A3 3; 4;1 , A4 2;3;6 .

1.29A1 8; 2;9 , A2 7;5; 3 , A3 7;4; 3 , A4 2;1;3 .

1.30A1 4;1;2 , A2 8;7;1 , A3 6;4;3 , A4 2;3; 1 .

V. Екінші ретті қисықтар және олардың канондық теңдеулері

Декарттық координаталар жүйесінде екінші дәрежелі теңдеумен анықталған келесі қисықты (сызықты) қарастырамыз

Ax2 2Bxy Cy2 2Dx 2Ey F 0

(5.1)

мұндағы A, B және C коэффициенттері ең кемінде біреуі нөлге тең емес нақты сандар. Мұндай сызық екінші ретті қисықтар (сызықтар) деп аталады. Қарастырып отырған (5.1) теңдеуі жазықтықта екінші ретті қисықтың арнайы түрлері шеңбер, эллипс, гипербола және параболаны анықтайды. Енді осы қисықтарды анықтайтын теңдеулерді қарастырып оларды зерттейміз.

5.1Шеңбер

5.1.1Шеңбердің канондық теңдеуі

1-анықтама. Центр деп аталатын берілген M0 нүктесінен бірдей қашықтықта жататын жазықтық барлық M нүктелерінің жиыны шеңбер деп аталады.

66

y

M x, y

R

y0 M0 x0, y0

Берілген M x0,y0 нүктесінен бірдей қашықтықта

жататын жазықтықтың кезкелген M x,y				нүктесіне
дейінгі	арақашықтық	шеңбердің	радиусы деп
аталады және R арқылы белгіленеді (6-сурет).
Шеңбердің	радиусын	табу үшін,	екі	нүктенің

арақашықтығын табу формуласын қолданамыз, сонда

O	x	R		M0M		(x x0)2 (y y0)2
10-сурет		теңдеуін аламыз. Осы теңдеудің екі жағын квадраттау
арқылы,		(x x0)2 (y y0)2 R2
							(5.2)
теңдеуі алынады.	Бұл теңдеу шеңбер бойында жататын кез келген						M x,y

нүктесінің координаттарын қанағаттандырады және шеңбердің канондық теңдеуі деп аталады.

Егер x0 0	және y0 0 болатын болса,	онда	центрі	координаттар
жүйесінің бас нүктесінде жататын шеңбердің дербес түрін аламыз
	x2 y2 R2.			(5.3)
Енді (5.2) теңдеуінде жақшаларды ашып, түлендіретін болсақ мына
теңдеуді аламыз	x2 y2 2x0x 2y0 y x02 y02	R2
			0.	(5.4)

Осы теңдеуді екінші ретті қисықтардың (5.1) жалпы теңдеуімен салыстыра отырып:

1)x2 және y2 коэффициенттерінің бірдей болатындығын,

2)x және y координаталары көбейтіндісінің жоқтығын көреміз,

яғни екінші ретті қисықтардың (5.1) жалпы теңдеуі шеңбердің теңдеуі болу үшін, B 0 және A C 0 болуы керек, сонда

Ax2 Ay2 2Dx 2Ey F 0

(5.5)

теңдеуі алынады. Осы теңдеуді түрлендіру арқылы

x

2

y

2

D

x

E

y

F

2

2

0

A

A

A

теңдеуін, ал бұл теңдеуді x және y

айнымалыларының толық квадратына

келтіре отырып,

D2

2

D2

E2

x

2

2D

x

y

2

2

E

y

E

F

0

A

A2

A2

яғни

A A2

A A2

D 2

2

E

E2

D2

F

x

y

(5.6)

A

A2

A2

A

A

теңдеуін аламыз.

67

E2

D2

F

D

E

Бұл теңдеу

0

болғанда, центрі O

;

, ал радиусы

A2

A2

A

A

A

R

E2

D2

F

болатын шеңбердің теңдеуін береді. Егер (5.6) теңдеуінде

A2

A2

A

E2

D2

F

0 болса, онда

A2

A2

A

2

E 2

D

x

y

0

A

A

D

E

теңдеуі центрі

O

;

нүктесі болатын,

ал радиусы нөлге тең «нөлге

A

A

айналған шеңберді» береді. Егер

E2

D2

F

0 болса,

онда (5.6) теңдеуі

A2

A2

A

ешбір сызықты анықтамайды, себебі теңдеудің оң жағы теріс, ал сол жағы оң болады, мұндай кезде (5.6) теңдеуі «жалған шеңбер» деп аталады.

	y		Жоғарыдағы (5.3)			теңдеуінен	шеңбердің
	y	M x, y	параметрлік	теңдеуін	шығарып алуға		болады. Ол
		R	үшің шеңбердің кезкелген M x,y нүктесінің радиус-
		t	векторы Ox	өсінің	оң	бағытымен	t бұрышын
	0	x x	0 t 2 жасайды деп ұйғарайық (10-сурет). Сосын

tбұрышын айнымалы параметр деп алып, ағымдағы x және y координаталарын параметр t арқылы

11-сурет	өрнектеуге болады:
	x R cost	.	(5.7)
	y R sint

Осы соңғы теңдеулер жүйесі шеңбердің параметрлік теңдеуі деп аталады.

Мысалы, x2 y2 8x 2y 21 0 шеңбердің центрін және радиусын анықтаңыздар.

Шешуі: Берілген теңдеу шеңбердің теңдеуін анықтайды. Себебі жоғарыда айтылған екі шарт орындалады, яғни x2 және y2 коэффициенттері бірдей, ал x және y координаталары көбейтіндісі жоқ. Теңдеуді x және y айнымалыларының толық квадратына келтіреміз:

x2 8x 16 y2 2y 1 21 0 x 4 2 y 1 2 4,

демек, берілген шеңбердің центрі O 4;1 нүктесі, ал радиусы R 2 болады.

68

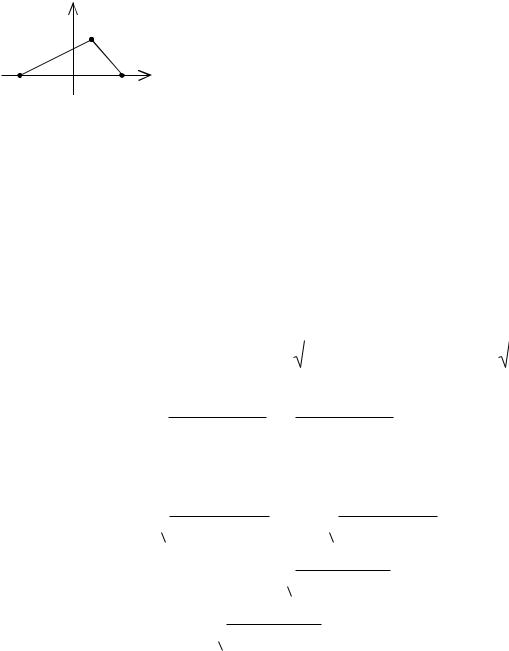
5.2Эллипс

5.2.1Эллипстің канондық теңдеуі

2-анықтама. Фокустар деп аталатын берілген екі F1 және F2 нүктелерінен қашықтықтарының қосындысы тұрақты 2a-ға, ал берілген фокустардың арақашықтығы 2c-ға тең болатын және 2a 2c теңсіздігін қанағаттандыратын жазықтықтың барлық нүктелерінің жиыны эллипс деп аталады.

Эллипстің теңдеуін қорытып шығару үшін F1 және F2 нүктелерін Ox өсінде жатқызамыз, ал декарттық координаталар жүйесінің бас нүктесін F1F2

y

M x,y r1 r2

F c,0 0	F c,0 x
1	2

12-сурет Айталық M x,y

кесіндісінің ортасына орналастырамыз (12-сурет). Сонда анықтама бойынша фокустардың арақашықтығы F1F2 2c болғандықтан, F1 және F2 нүктелерінің координаталары сәйкес түрде F1( c; 0) және F2( c; 0)болады.

ізделінді эллипстің кезкелген нүктесі болсын. Онда

анықтама бойынша F1M F2M 2a, мұндағы F1M r1 және F2M r2 арқылы белгілейміз де, оларды M нүктесінің сәйкес сол жақ және оң жақ фокальдық радиус-векторлары деп атаймыз. Сонымен

r1 r2 2a							(5.8)
теңдігігің орындалуы, M нүктесінің эллипсте жатуының					қажетті		және
жеткілікті шарты болып табылады.
Екі нүктенің арақашықтығын табу формуласын қолданыу арқылы,
эллипстің фокустары F1 және F2	нүктелерінен,			берілген	M нүктесіне
дейінгі арақашықтықтар сәйкес r		x c 2 y2		және r		x c 2	y2
1				2

теңдеулерімен анықталатынын көреміз. Осы теңдеулерді (5.8) теңдеуіне қоятын болсақ,

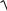
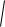x c 2 y2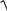 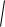x c 2 y2 2a (5.9)

теңдеуін аламыз. Бұл біз іздеп отырған эллипстің теңдеуі болады. Енді (5.9) теңдеуін қарапайым түрге келтіру үшін, ең алдымен теңдеуді келесі түде жазамыз, сонда

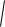(x c)2 y2 2a 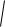(x c)2 y2

теңдеуі шығады. Осы теңдеудің екі жағын квадраттаймыз, сонда x2 2cx c2 y2 4a2 4a 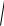(x c)2 y2 x2 2cx c2 y2

теңдеуін аламыз, енді осы теңдеудің ұқсас мүшелерін біріктіру арқылы a(x c)2 y2 a2 cx

теңдеуін шығарамыз. Бұл теңдіктің екі жағын тағы бір рет квадраттап, ұқсас мүшелерін біріктіре отырып келесі теңдеуді аламыз

69

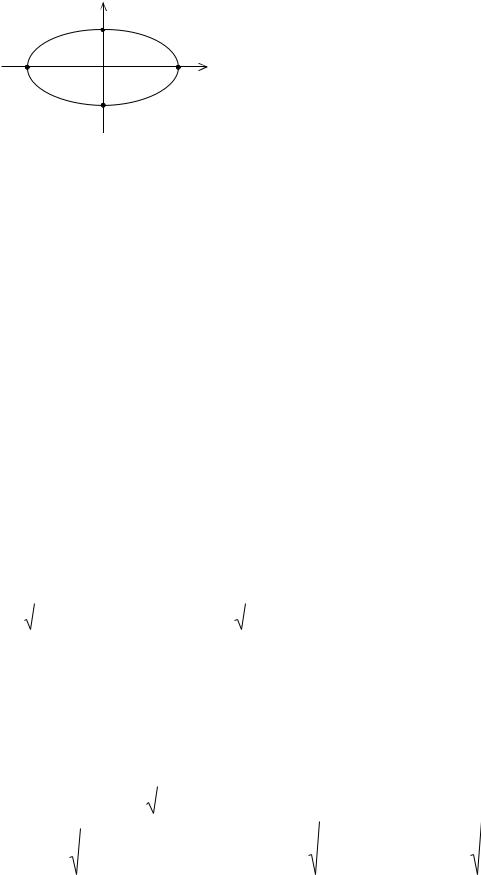
a2x2 2a2cx a2c2 a2y2 a4 2a2cx c2x2 ,

(a2 c2)x2 a2 y2

a2(a2 c2).

(5.10)

Анықтамадан a c

болғандықтан,

a2 c2

0

болады, оны b2 арқылы

y

белгілейміз, яғни

b

a

2

c

2

b

2

a

өрнегін аламыз. Осы өрнекті (5.10)

теңдеуіне

a

x қою арқылы келесі теңдеуді аламыз

0

b

b2x2 a2 y2 a2b2.

Осы

теңдіктің

екі

жағын

a2b2

өрнегіне

13-сурет

бөлеміз, сонда

x2

y2

1

(5.11)

a2

b2

теңдеуі алынады. Бұл теңдеу эллипстің канондық теңдеуі деп аталады. Осы теңдеудегі a эллипстің үлкен жарты өсі, ал b оның кіші жарты өсі деп аталады a b (13-сурет).

Эллипстің канондық теңдеуін зерттеу барысында келесі ескертулер кездеседі.

1-ескерту. Егер (5.11) теңдеуінде a b болса, онда x2 y2 a2 теңдеуі, центрі координат жүйесінің бас нүктесінде болатын, радиусы a-ға тең шеңбер теңдеуін береді. Демек шеңбер теңдеуін эллипс теңдеуінің a b болғандағы дербес түрі деп қарауға болатындығын көреміз.

2-ескерту. Жоғарыда көрсетілгендей (5.11) теңдеуін қорытып шығару барысында алгебралық түрлендірулер кезінде түбірден құтылу үшін екі рет квадраттау амалын қолдандық. Сол себебті (5.11) теңдеуін қанағаттандыратын түбірлерінен басқа «бөгде» түбірлер қосымша пайда

болуы мүмкін.

Сондықтан осындай «бөгде» түбірлердің жоқтығын дәлелдеу үшін (5.11)

теңдеуін қанағаттандыратын кезкелген M(x, y)

нүктесі эллипсте жататынын

көрсетуіміз

керек. Ол үшін

(5.11)

теңдеуін

y2

арқылы өрнектеп,

оны

r

x c 2

y2

және

r

x c 2

y2

теңдіктерінің

оң

жағына

қоя

1

2

отырып тексереміз.

b2

(5.11) теңдеуінен y

2

(a

2

x

2

) болады, енді b

2

a

2

c

2

болатынын

a2

ескерсек,

a2

c2

c2

y

2

(a

2

x

2

)

немесе y

2

a

2

c

2

x

2

x

2

.

a2

a2

Соңғы өрнекті r

x c 2

y2

теңдеуіндегі y2 -тың орнына қойсақ,

1

c

2

c

2

c

2

r x c 2

a2 c2

x2

x2

a2 2cx

x

a

x .

1

a2

a

a

70

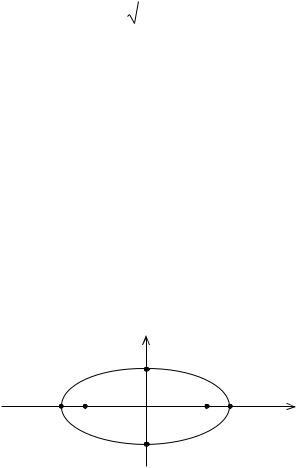
Мұндағы

a

c

x 0 болғандықтан

(

x

a және

c

1),

r a

c

x. Дәл

a

a

1

a

c

осындай жолмен r a

x болатынын табамыз.

2

a

Сонымен қарастырылып отырған M(x, y) нүктесі үшін

r

a

c

x,

r a

c

x,

(5.12)

1

a

2

a

яғни r1 r2

2a болады да,

M(x, y) нүктесінің эллипсте жататынын көреміз.

(5.12) теңдеуі эллипстің фокальдық радиус-векторларының теңдеуі болып табылады.

5.2.2 Эллипстің пішінін оның канондық теңдеуі бойынша зерттеу

Эллипстің канондық теңдеуінен

b

y

a

2

x

2

(5.13)

a

теңдеуін алып, осы теңдеуге зерттеу жүргізейік.

A2 a,

0

1.

Егер

y 0

болса,

онда

x a,

яғни

A1 a, 0 ,

нүктелерін

аламыз. Бұлар өзара симметриялы абсцисса бойында жатқан эллипстің

нүктелері;

B1 0, b ,

B2 0, b

2.

егер

x 0

болса,

онда

y b,

яғни

нүктелерін

аламыз. Бұл нүктелер эллипстің ордината бойында жатқан өзара

симметриялы нүктелері;

a2 x2 0

3.

(5.13)

теңдеуі

x

a

мәндерінде

ғана орын алады, себебі

болуы керек. Осыдан

x2 a2,

ал

x

a

олай болса, (5.13)

теңдеуінен

y

b

болады

да,

эллипс

қабырғалары

2a

және

2b

болатын

тіктөртбұрыштың

ішінде

жатады

деген

тұжырымға

келеміз, яғни

a x a болса, онда

b y b (14-сурет);

y

B2 0;b

A a;0

F1

0

F2

A a;0

x

1

2

B1 0; b

14-сурет

4.a2 c2 b2 теңдігінен анықтама бойынша a c болғандықтан, a b. Бұл жерде 2a эллипстің үлкен өсі, ал 2b оның кіші өсі, 2c эллипстің фокустық аралықтары екендіктерін ескере кетейік;

5.(5.11) эллипстің канондық теңдеуі ағымдық координаталардың квадраттарынан ғана тұратын болғандықтан, координат өстері эллипстің симметрия өстері болады;

71

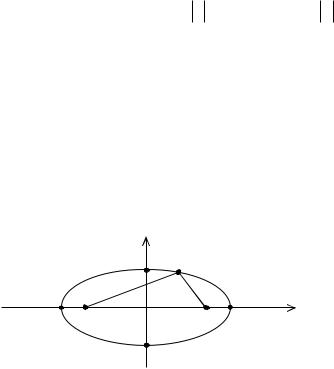
	6. (5.11) эллипстің канондық теңдеуінде теріс емес	x2	және	y2
		a2		b2

қосылғыштарының қосындысы бірге тең. Сондықтан бір қосылғыш өсетін болса, екінші қосылғыш кемиді, яғни x өссе, онда y кемиді және

керсінше.

Эллипстің фокустары орналасқан симметрия өсі эллипстің фокустық өсі деп аталады. Эллипстің симметрия өстерінің қиылысу нүктесі эллипстің центрі деп аталады. (5.11) теңдеуімен берілген эллипс үшін фокустық өс абсцисса өсімен беттеседі, ал координат басы O 0, 0 эллипстің центрі болады (14-сурет). Эллипстің симметрия өстерімен қиылысу нүктелері

A1 a,0 , A2 a,0 , B1 0, b және B2 0,b эллипстің төбелері деп аталады

(14-сурет). Осы зерттеулердің нәтижесіне сүйене отырып, эллипстің пішінін сызып көрсетуге болады (15-сурет).

y

			B2	0;b
		r1		M r
					2		x
A a;0		F1	0		F2	A a;0
1						2
			B1	0;b
		15-сурет
Суреттен анықтама	бойынша		r1 r2		2a ,		A1A2 2a,	B1B2 2b,

F1F2 2c болатынын, сондай-ақ F1M F2M 2a екенін көруге болады. Эллипсті механикалық түрде де сызуға болады. Ол үшін ұзындығы 2a-

ға тең жіп алып, оның екі ұшын қозғалмайтын F1 және F2 нүктелеріне бекітіп, сонан соң қалам ұшымен жіпті кере жүргізіп отырсақ, онда қалам ұшы берілген эллипсті сызып шығады.

5.2.3 Эллипстің радиус-векторы, эксцентриситеті және директрисасы

Эллипстің фокальдық радиус-векторларының теңдеуін қайта қарастырамыз:

	r	a		c	x және r			a	c	x.	(5.14)
	1			a	2				a
		c
	Осы теңдеулердегі		шамасы эллипстің эксцентритеті деп аталады
		a
	және оны («эпсилон») арқылы белгілейміз:
						c	.				(5.15)
						a

72

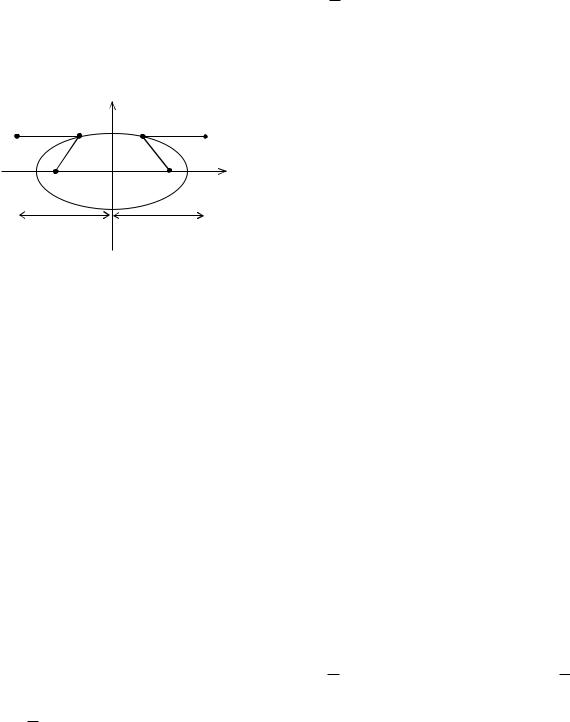
Бұл теңдіктен эллипстің эксцентриситеті оның фокустар аралығы 2c- ның, эллипстің үлкен өсі 2a-ға қатынасына тең екенін көреміз. Ал 0 c a

болғандықтан, 0 1 болады, яғни c 1. a

(5.15) теңдігін пайдаланып (5.14) теңдеулерін эксцентриситет арқылы мына түрде жазамыз

r1 a x және r2

a x.

(5.16)

y

d2

l

Эллипске қатысты тағы бір түсінік беру

d

M

үшін

Oy

өсіне

параллель x l

(l a)

1

түзуін

жүргіземіз.

Эллипстің

кезкелген

F1

0

F2

x

M(x, y) нүктесінен

x l түзуіне

дейінгі

a

арақашықтықты d2 деп белгілеп, эллипстің

a

оң

жақ

фокусы

мен

M(x, y)

нүктесінің

арасындағы

қашықтық

r2-нің осы d2 -ге

16-сурет

қатынасын қарастырамыз (16-сурет). Белгілеу

бойынша d2 l x

болғандықтан,

a

r2

a x

x

d2

теңдеуі орындалады.

l x

l x

a

r2

Бұл теңдеуде егер

l

болатын болса, онда

қатынасы

ге тең

d2

тұракты шама болады, яғни

r2

(5.17)

теңдігі орындалады.

d2

Эллипстің фокустары координат басына қарағанда симметриялы

орналасқандықтан, сол жақ фокус

F

мен

x

a

теңдеуімен берілген түзу

1

үшін де дәл осындай тұжырым жасауға болады. Эллипстің фокустық өсіне

перпендикуляр болатын оның центрінен a қашықтықта жатқан x a және

x a түзулері эллипстің директрисалары деп аталады.

5.3Гипербола

5.3.1Гиперболаның канондық теңдеуі.

3-анықтама. Фокустар деп аталатын берілген екі F1 және F2 нүктелернен қашықтықтары айырымының абсолют шамасы тұрақты 2a-ға,

73

ал берілген фокустардың арақашықтығы 2c-ға тең болатын және 2a 2c теңсіздігін қанағаттандыратын жазықтықтың барлық нүктелерінің жиыны гипербола деп аталады.

Гиперболаның канондық теңдеуін қорытып шығару үшін F1 және F2 нүктелерін Ox өсінде жатқызамыз, ал декарттық координаталар жүйесінің бас нүктесін F1F2 кесіндісінің ортасына орналастырамыз (17-сурет). Сонда анықтама бойынша фокустардың арақашықтығы F1F2 2c болғандықтан,

	y		F1 және F2 нүктелерінің координаталары сәйкес
		M x,y	түрде F1( c; 0)	және F2( c; 0) болады. Ал M x,y
			ізделінді гиперболаның кезкелген нүктесі болсын.
		r1
		r2	Осы нүктенің	F1	және		F2 фокустардан
	F c,0 0	F c,0 x
			қашықтықтары	сәйкес	F1M r1		және F2M r2
	1	2
	17-сурет		арқылы белгіленеді де,		олар	M нүктесінің сәйкес

сол жақ және оң жақ фокальдық радиус-векторлары деп аталады. Сонымен гиперболаның анықтамасы бойынша

r1 r2

2a

(5.18)

теңдігі орындалады. Бұл теңдік

M

нүктесінің

гиперболада

жатуының

қажетті және жеткілікті шарты болады.

Жоғарыда 5.2.1 бөлімінде

көрсетілгендей

r

(x c)2

y2

және

1

r

(x c)2 y2

болатындығын

білеміз. Оларды

енді (5.18)

формулаға

2

қоятын болсақ,

(x c)2 y2

(x c)2 y2

2a

(5.19)

теңдеуін аламыз. Бұл теңдеу біз қарастырып отырған координат жүйесіндегі гиперболаның теңдеуі болады. Енді (5.19) теңдеуін қарапайым түрге келтіру үшін, алдымен теңдеуді келесі түде жазамыз, сонда

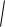(x c)2 y2 2a 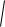(x c)2 y2

теңдеуі шығады. Осы теңдеудің екі жағын квадраттаймыз, сонда x2 2cx c2 y2 4a2 4a 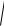(x c)2 y2 x2 2cx c2 y2

теңдеуін аламыз, енді осы теңдеудің ұқсас мүшелерін біріктіп, теңдеудің екі жағын төртке бөлу арқылы

cx a2 a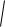(x c)2 y2

теңдеуін шығарамыз. Бұл теңдеудің екі жағын тағы бір рет квадраттап, ұқсас

мүшелерін біріктіре отырып мына теңдеуді аламыз:
c2x2 2a2cx a4 a2x2 2a2cx a2c2 a2 y2 ,
(c2 a2)x2 a2 y2 a2(c2 a2).		(5.20)
Гиперболаның анықтамасынан c a болғандықтан,	c2 a2	0 болады,
оны b2 арқылы белгілейміз, яғни
c2 a2 b2		(5.21)
74

өрнегін аламыз. Осы өрнекті (5.20) теңдеуіне қою арқылы келесі теңдеуді аламыз

b2x2 a2 y2 a2b2 .

Осы теңдіктің екі жағын a2b2 өрнегіне бөлеміз, сонда

	x	2		y2	1	(5.22)
	a2			b2

теңдеуін аламыз. Осы шыққан теңдеу гиперболаның канондық теңдеуі деп аталады. Мұндағы a гиперболаның нақты жарты өсі, ал b оның жорамал жарты өсі деп аталады (18-сурет).

y

		b	r1		M x,y
F	a		a	F	r2
		0			x
1				2
		b

18-сурет 3-ескерту. Жоғарыда (5.22) теңдеуін қортып шығару барысында

алгебралық түрлендірулер кезінде түбірден құтылу үшін екі рет квадраттау амалын қолдандық, сондықтан (5.22) теңдеуінде оны қанағаттандырмайтын «бөгде» түбірлер пайда болуы мүмкін.

Осындай «бөгде» түбірлердің жоқтығына көз жеткізу үшін координаталары (5.22) теңдеуін қанағаттандыратын кезкелген M(x, y) нүктесі гиперболада жататынын дәлелдеу керек.

Ол үшін (5.22) теңдеуін y2 арқылы өрнектеп, оны r1 x c 2 y2 және r2 x c 2 y2 теңдеулерінің оң жағына қоя отырып тексереміз.

(5.22) теңдеуінен

y

2

b2

(x

2

a

2

) болады, енді b

2

c

2

a

2

болатынын

a2

ескерсек,

c2 a2

c2

y

2

(x

2

a

2

)

немесе y

2

x

2

x

2

c

2

a

2

.

a2

a2

Соңғы өрнекті r

x c 2

y2

теңдеуіндегі y2 -тың орнына қойсақ,

1

2

2

r x c 2

c2

x2 x2 c2

a2

a2 2cx

c

c

x

a

x .

1

a2

a

a

Мұндағы

a

c

x 0

болуы

керек,

анықтама

бойынша

c

1

a

a

болғандықтан,

x 0 болғанда r

a

c

x

және

x 0

болғанда r

a

c

x

1

a

1

a

75