Оулы 1-2

III.Векторлық алгебра

3.1Векторлар және оларға қолданылатын амалдар

1-анықтама. Бағытталған кесiндi вектор деп аталады.

Вектордың басы A нүктесiнде, ал соңы B нүктесi болса, онда вектор AB болып белгiленедi. Егер вектордың басы және соңы көрсетiлмесе, онда вектор латын әліппесінің кiшi әрiптерi a,b,c,... арқылы белгiленедi. Төменгi 5-суретте вектордың бағыты ұшталып белгiленген.

a	b	B

AB

A

5-сурет

AB векторына қарсы бағытталған вектор BA деп белгiленедi. Басы және соңы беттесетiн вектор нөлдiк вектор деп аталады және 0 деп белгiленедi. Оның бағыты белгiсiз болады.

2-анықтама. Вектордың ұзындығы немесе модулi деп оның басы мен соңының арасындағы арақашықтық аталады және мына түрде белгiленеді AB және a .

3-анықтама. Вектордың ұзындығы AB және a оның нормасы деп

аталады.

4-анықтама. Ұзындығы бiрге тең вектор – бiрлiк вектор немесе орт деп аталады.

5-анықтама. Векторлар бiр түзуге параллель болса, онда олар коллинеар деп, ал бiр жазықтыққа параллель болса, онда олар компланар деп аталады.

6-анықтама. Өзара коллинеарлы, ұзындықтары бiрдей, ал бағыттары қарсы болатын a және b векторы қарама-қарсы векторлар деп аталады және a b, ( a b) түрiнде жазылады.

7-анықтама. Екi вектор коллинеар, бiр бағыттас және ұзындықтары бойынша тең болса, онда олар тең векторлар деп аталады. Тең векторлар AB CD немесе a b болып жазылады.

Векторларға қолданылатын сызықтық амалдарға векторды санға көбейту

және векторларды өз ара қосу жатады.
8-анықтама. Модулi a болатын,	0 болғанда a векторымен

бағыттас, ал 0 болғанда a векторымен қарама-қарсы бағыттас вектор a векторының санына көбейтiндiсi деп аталады және a немесе a болып белгiленеді.

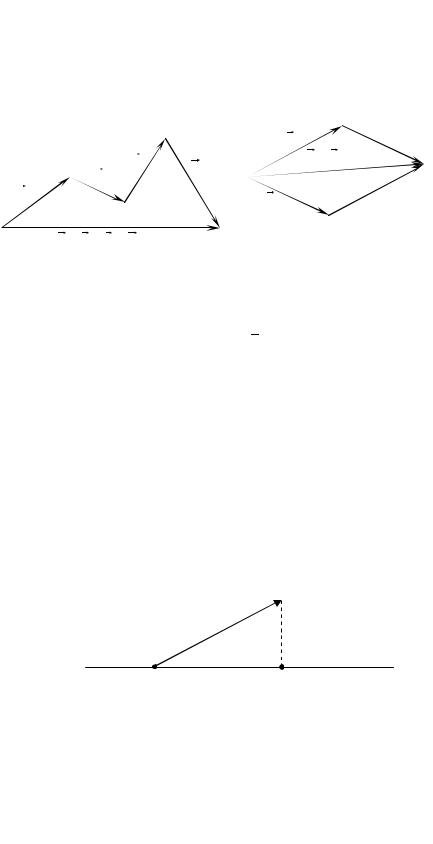
9-анықтама. Басы сынық сызықтардың бiрiншi векторының басы, ал соңы соңғы векторының соңы болатын вектор ai (i 1,n) векторларының

43

	n
қосындысы деп аталады және a1 a2 ... an	ai болып белгiленеді.
	i 1

Векторларды мұндай қосу әдiсi қисықтарды тұйықтау ережесi деп аталады (6а-сурет). Егер екі вектор бір нүктеден шығатын болса, онда оларды параллелограмм ережесi деп аталатын әдіс бойынша қосамыз (6ә-сурет).

					a
	c		d				a b
	b
a
					b
	a b c d
	6а-сурет				6ә-сурет
Бағытымен берiлген l түзуi оң деп қабылданады және l өсi деп аталады.
10-анықтама. Шамасы		a	cos	тең	сан, a векторының l өсiндегi
проекциясы	деп аталады	және		прl a	болып белгiленеді, мұндағы
(0 )	- l өсiнiң оң бағытымен a				векторының бағыты арасындағы
бұрыш, яғни	анықтама бойынша			прl a	=		a		cos болып белгіленеді.

Геометриялық тұрғыдан a векторының l өсiндегi проекциясын, осы өстiң бойындағы MN кесiндiсiнiң ұзындығы деп сипаттауға болады (7-сурет). Егер

0		болса, онда бұл	ұзындық «+» таңбасымен, ал егер
2			2
болса,онда бұл ұзындық «-»			таңбасымен алынады. Егер		болса, онда
			2
MN кесiндiсi нүктеге айналады және прl a = 0 болады.

a

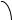
l	M	N
	7-сурет
11-анықтама. a	векторының декарттық координаттар Ox, Oy, Oz
өстерiндегi ортогональдық проекциясы, a		вектордың координатасы деп
аталады. Олар сәйкес x,	y, z әрiптерiмен белгiленiп және a x;y;z түрiнде

жазылады.

Векторлар тең болу үшiн олардың сәйкес координаталарының тең болуы

қажеттi және жеткiлiктi болып табылады. Мәселен,		егер a b болса,	онда
ax bx , ay by және az	bz болады және керсінше.
Егер нүктелер	координаталарымен берiлсе	M1(x1, y1,z1)	және
M2(x2, y2,z2), онда

44

M1M2 x2 x1;y2 y1;z2 z1

(3.1)

болады, яғни екi нүктенi қосатын вектордың координатасы соңғы нүктенiң координатасынан, бас нүктенiң сәйкес координаттарын алғанға тең.

n

12-анықтама.

a iai

формуласымен анықталатын

вектор ai

i 1

i

векторларының сызықтық комбинациясы деп аталады, мұндағы i

1,n

қандайда бiр нақты сандар болып табылады.

Егер

ai

векторлары xi, yi,

zi

координаталарымен анықталған болса,

онда

a

векторының

n

n

n

түрiнде

координатасы a

ixi; i yi; izi

анықталады.

i 1

i 1

i 1

Егер ai

векторларның n жүйесi үшiн

n

i ai 0

(3.2)

қана i

0

i 1

теңдiгi

тек

болғанда

орындалса,

онда бұл

теңдеулер

жүйесi

сызықтық тәуелсiз деп аталады. Егер (3.2) теңдеуі ең кемiнде бiреуi нөлге тең емес i үшiн орындалса, онда теңдеулер жүйесi сызықтық тәуелдi деп аталады. Мысалы, кез келген екi коллинеар векторлар, үш компланар векторлар, төрт және одан да көп үш өлшемдi кеңiстiктiң векторлары сызықтық тәуелдi болады.

13-анықтама. Кеңiстiктегi		сызықтық тәуелсiз	реттелген үш	вектор
e1,e2,e3	базис деп аталады.
Компланар емес векторлардың реттелген үштiгi әр уақытта базис
құрайды.	Үш компланар емес	e1 x1, y1,z1 ,	e2 x2, y2,z2	және

e3 x3, y3,z3 векторлары базис құрайды, егер олардың координаталарынан құралған анықтауыш нөлге тең емес болса, яғни

	x1	y1	z1
	x2	y2	z2	0		(3.3)
	x3 y3 z3
болады.			e1,e2,e3
Кеңiстiктегi кез келген векторды					базисi бойынша	жiктеп
жазуға болады, яғни a векторын			базистiк		векторлардың сызықтық
комбинациясы түрiнде жазуға болады			a xe1 ye2 ze3 , мұндағы			x, y, z
шамалары a векторының сәйкес e1,e2,e3			базисiндегi координаттары.
Егер базистің векторлары өз ара перпендикуляр және ұзындықтары бiрге
тең болса, онда олар ортонормальды деп аталады және i, j,k						болып
белгiленеді.

45

Мысалы, тiкбұрышты Oxyz координаталар жүйесiнде берiлген a

векторын мына түрде жазамыз a axi ay j az k мұндағы ax,ay,az

шамалары a векторының сәйкес Ox,Oy,Oz өстерiндегi координаттары, яғни

a ax,ay,az болады. Осы вектордың ұзындығы

a

ax2 ay2 az2

формуласымен есептелінеді.

Векторларға жүргiзiлетiн сызықтық амалдар, сандарға қолданылатын

қосу және көбейту амалдары қасиеттерiн қанағаттандырады.
Мысалы,	a b b a,	( )a a a,		(a b) a b,
(a b) c a (b c), a ( a) 0, a 0 a,			1a a,	0a 0 т.с.с.
Егер a ax,ay,az және		b bx,by,bz болса, онда бұл екi вектордың
қосындысы	a b ax bx,ay by,az bz		түрiнде		болады,	ал

a ax,ay,az векторын қандайда бiр санына көбейту a ax, ay, az түрiнде жазылады.

3.2 Скалярлық көбейту.

14-анықтама. a және b векторларының ұзындықтары мен олардың арасындағы бұрыштың косинусының көбейтiндiсiне тең сан, a және b векторларының скалярлық көбейтiндiсi деп аталады және былай жазылады:

a b abcos .

(3.4)

Скалярлық көбейтiндi қасиеттерi.

a)a a a2 немесе a2 a2.

b)a b 0, егер a 0, не b 0, не a b (нөлге тең емес векторлардың ортогональдық белгiсi).

c)a b b a (ауыстырымдылық заңы).

d)a (b c) a b a c (үлестірiмдiлiк заңы).

e) (ma) b a (mb) m(a b)(скалярлық көбейтiндiге қатысты терiмдiлiк заңы).

Координата өстерiнiң орттарын скалярлық көбейту мына түрдегі i2 j2 k2 1, i j i k j k 0

формуламен анықталады.

Сондықтан, егер a және b векторлары өздерiнiң координаталарымен берiлсе, яғни a x1i y1 j z1k және b x2i y2 j z2k болса, онда a b x1x2 y1y2 z1z2 болады.

46

3.3 Векторлық көбейту

15-анықтама. a векторының b векторына векторлық көбейтiндiсi деп

келесi түрде анықталатын үшiншi бiр c векторы аталады:
1) c векторының	модулы	a	және b векторларына							тұрғызылған
параллелограммның	ауданына	тең	(	c		a	b	sin , мұндағы		a және b

векторларының арасындағы бұрыш, бұл бұрыш сағат тіліне қарама қарсы бағытта алынады).

2)c векторы a және b векторларына перпендикуляр;

3)a,b,c векторлары бiр бастауға келтiрілген кезде, егер a векторының b векторына векторлық көбейтіндісі сағат тіліне қарама қарсы бағытта алынса, онда олар бiр бiрiне қатысты сәйкес i, j,k орттарындай орналасады және оң

үштiк құрайды (8-сурет), ал егер векторлық көбейтінді сағат тілімен бағыттас алынса сол үштiк құрайды (9-сурет).

							b
	c	b				c	a
		a
	8-сурет (оң үштік)					9-сурет (сол үштік)
	Ал, a және b векторларының векторлық						көбейтiндiсi a b			түрiнде
белгiленедi.
	Векторлық көбейтiндi қасиеттерi.
а)	b a a b	яғни векторлық көбейтуде орын ауыс-тырымдылық заңы
орындалмайды.
в)	a b 0, егер		a 0, не	b 0,	не a b (нөлдiк			емес векторлардың
коллинеарлық шарты).
с)	ma b a mb m a b			(скалярлық көбейткiшке				қатысты	терiмдiлiк
заңы орындалады).
д) a b c a b a c (үлестiрiмдiлiк заңы).
	Координаттың		орттары	i, j	және k	векторлық көбейтуде				мына
қасиеттер орындалады:
			i i j j k k 0
	i j j i k;			j k k j i; k i i k j.
	Векторлар	a x1i y1 j z1k			және	b x2i y2		j z2k	векторлық

көбейтудi мына формуламен жазу ыңғайлы болады:

	i	j	k
a b	x1	y1	z1	.	(3.5)
	x2	y2	z2

47

	3.4 Аралас көбейту
16-анықтама. a b	векторының c векторына скаляр көбейтiндiсi a, b
және c векторларының	аралас көбейтiндiсi деп аталады және a b c
арқылы белгіленеді.

Ал a, b, c үш векторларының аралас көбейтiндiсiнiң модулы осы үш векторға тұрғызылған параллелепипедтiң көлемiне тең.

Аралас көбейтудiң қасиеттерi.

1)Егер үш вектор үшін мына шарттар орындалса:

a)ең кемiнде көбейткiш векторлардың бiреуi нөлге тең болса;

b)көбейткiш векторлардың екеуi коллинеарлы болса;

c)нөлдiк емес үш вектор бiр жазықтыққа параллель болса (компланарлы);

онда үш вектордың аралас көбейтiндiсi нөлге тең.

2)Егер аралас көбейтуде векторлық және скалярлық көбейткiштердiң

орындарын ауыстырсақ, одан көбейтiндi өзгермейдi, яғниa b c a b c . Сондықтан осы қасиеттердi пайдаланып a, b және c

векторларының аралас көбейтiндiсiн мына түрде жазуға келiсемiз abc.

3)Егер аралас көбейтуде көбейткiш векторлардың орындарын айналдыра ауыстырсақ одан көбейтiндi өзгермейдi:

abc bca cab.

4)Аралас көбейтуде кез келген екi вектордың орынын ауыстырсақ, онда көбейту таңбасы ауысады:

bac abc; cba abc; acb abc.

Егер векторлар орттарға жiктелу арқылы берiлсе:

a x1i y1 j z1k; b x2i y2 j z2k; c x3i y3 j z3k,

онда олардың аралас көбейтіндісі

	x1	y1	z1
abc	x2	y2	z2	(3.6)
	x3	y3	z3

анықтауышы арқылы есептелінеді.

Үш вектордың аралас көбейтiндiсi қасиеттерiнен мына тұжырымдар шығады:

үш вектор компланар болу үшiн abc 0 шартының орындалуы қажеттi және жеткiлiктi болып табылады;

a, b және c векторларына тұрғызылған параллелепипедтiң V1 көлемi және

солармен жасалынған үш бұрышты пирамиданың V2 көлемi келесi формулалар арқылы табылады:

V		abc		,	V	2		1	V		1			abc		.	(3.7)
1							6		1	6
							48

в) VABCD

Мысалы,

пирамиданың

төбелерi

A(1; 1;2), B(2;1;2), C(1;1;4) және

D(6; 3;8) берiлген. Есептеңіз: а)

AB

; ә)

BC BD; б) S ABC ;

в) VABCD.

Шешуі: а)

AB

табу үшiн, ең алдымен AB табамыз:

AB (2 1)i (1 1)j (2 2)k i 2j, онда

AB

болады.

1 4

5

ә)

BC BD

скалярлық көбейтуiн

анықтау үшiн, BC және BD

векторларының координаталарын табамыз:

BC (1 2)i (1 1)j (4 2)k i 2k

және

BD (6 2)i ( 3 1)j (8 2)k 4i 4j 6k , онда

BC BD 1 4 0 ( 4) 2 6 4 12 8 теңдігімен анықталады.

б)

S ABC

ауданы AB

және

AC

векторларының векторлық

көбейтiндiсiнiң модулiнiң жартысына тең. Сондықтан AB және AC векторларының координаталарын анықтаймыз:

AB (2 1)i (1 1)j (2 2)k i 2j және

AC (1 1)i (1 1)j (4 2)k 2j 2k, ендi осы екi вектордың векторлық көбейтiндiсiн табамыз:

AB AC	i	j	k		2	0		i		1	0		j		1	2		k 4i 2j 2k, сонда
	1	2	0
					2	2				0	2				0	2
	0	2	2

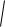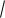AB AC 42 ( 2)2 22 16 4 4 24 2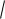6, демек

1

S ABC 2 2 6 6 тең.

көлемi пирамиданың қабырғаларына сәйкес келетiн AB,AC

және AD векторларының аралас көбейтiндiсiнiң модулiнiң 1-не тең. 6

AB (2 1)i (1 1)j (2 2)k i 2j,

AC (1 1)i (1 1)j (4 2)k 2j 2k және

AD (6 1)i ( 3 1)j (8 2)k 5i 2j 6k.

Сондықтан, осы үш вектордың аралас көбейтiндiсiн табамыз:

								1	2		0
	AB AC AD							0	2		2	12 0 20 0 4 0 36, онда
								5		2	6
	VABCD	1			36				1	36 6 болады.
	6								6

49

3.5 №3 өздiк жұмыс тапсырмалары

Пирамиданың төбелерi A(x1;y1;z1), B(x2; y2;z2), C(x3; y3;z3) және D(x4;y4;z4) берiлген. Есептеңіз: а) AB ; ә) BC BD; б) S ABC ; в) VABCD.

1.1A(2;4;5), B(1;3;7), C( 2; 3;6), D(9; 6;8) .

1.2A( 7;5;6), B( 2;8; 3), C(3; 9;4), D(1; 8;2).

1.3A(1;3;7), B(9;4;6), C( 2; 3;5), D( 5;8; 4).

1.4A(2;5;1), B( 3; 2;9), C(3; 5;6), D(4; 9;7) .

1.5A( 5; 3; 4), B(1;9;7), C(3;2;6), D(8; 2;4).

1.6A(3;4;2), B( 2;7; 5), C(9; 3;6), D(8;5;0) .

1.7A(8; 2;3), B(0; 5;7), C(2;4; 4), D(6; 8;5) .

1.8A(7;5;8), B( 4; 5;3), C(2; 3;9), D(6;1;4).

1.9A(9;2;6), B( 6; 2;3), C( 3;1; 4), D(4;5; 7) .

1.10A( 5; 4; 3), B(7;3; 1), C(6; 2;0), D( 6;2; 7).

1.11A(3; 5; 2), B( 4;2; 3), C(1;5;7), D( 8;4;9).

1.12A(7;4;9), B(1; 2; 3), C( 5;3;0), D(8; 7; 4).

1.13A( 4; 7; 3), B(0; 5;7), C(2;3;8), D(9; 2;1).

1.14A( 4; 5; 3), B(3;1;2), C(5;7; 6), D(6; 1;5).

1.15A(5;2;4), B( 3;8; 7), C(1; 5;7), D(9;3;6) .

1.16A( 6;4;5), B(9; 7;3), C(7;2; 8), D( 2;8; 3).

1.17A(5;3;6), B( 3; 4; 5), C(7; 6;8), D(4;0; 9).

1.18A(5; 4;4), B( 8; 6;7), C(3;2; 7), D(6; 2; 9).

1.19A( 7; 6; 5), B(5;1; 3), C(8; 4;0), D(3;4;7).

1.20A(7; 1; 2), B(1; 7;8), C(3; 8;9), D( 2; 5;2).

1.21A(5;2;7), B( 7; 6; 9), C( 8;6;3), D(1; 5; 2).

1.22A( 2; 5; 1), B( 6; 7;9), C(4;5;1), D(3;8;7).

1.23A( 6; 3; 5), B(5;1;7), C(3;2; 1), D(4; 2;9).

1.24A(7;4;2), B( 5;3; 9), C(1;5;8), D(6;9; 1).

1.25A( 8;2;7), B(3; 5;9), C( 9;4; 6), D( 4;6;5).

1.26A(4;3;1), B(2;7;5), C( 4; 2;8), D( 1; 3; 5).

1.27A( 9; 7;4), B( 4;3; 1), C(5;1;2), D( 3;8;9).

1.28A(3;5;8), B( 3;2;7), C(9; 2;6), D(1; 8; 9).

1.29A(4;2;3), B( 5; 4; 2), C(5;7; 8), D(6;9; 7).

1.30A(4; 2; 3), B(2;5;7), C(6;3; 1), D(9; 4;1).

50

IV. Жазықтықтағы және кеңiстiктегi аналитикалық геометрия

4.1 Жазықтықтағы аналитикалық геометрия

Егер жазықтықта тiк бұрышты xOy декарттық координаталар жүйесi берiлсе, онда осы жазықтықтың координаталары x және y болатын M нүктесi M(x;y) деп белгiленеді.

Жазықтықтың M1(x1;y1)			және	M2(x2;y2)			нүктелерiнiң арасындағы
арақашықтық
d	x	2	x 2	y	2	y 2	(4.1)
			1			1

формуласымен анықталады.

Жазықтықтағы A(x1;y1) және B(x2; y2) нүктелерiнiң арасын берiлген қатынасында бөлетiн C(x;y) нүктесiнiң координаттары

						x					x1 x2					;		y					y1		y2								(4.2)
формуласымен анықталады.												1												1
Егер C(x;y) нүктесi A(x1;y1)																		және							B(x2; y2) нүктелерiнiң ортасы
болса, онда									x1 x2													y1			y2
						x									;			y															(4.3)
																									2
												2
формуласымен есептелiнедi.
Төбелерi A(x1;y1), B(x2; y2) және C(x3;y3) болатын үшбұрыштың
ауданы
S		1				x (y						y		) x				(y		y ) x								(y y					)
2						1				2			3				2		3					1		3					1	2
	1			(x				x )(y							y			) (x						x )(y							y )		(4.4)
2							2					1		3			1				3				1				2		1

формуласымен есептелінеді.

(4.4) формуласын анықтауышты пайдаланып,

S 1 ,

2

мұндағы

1 1 1

x1 x2 x3 . y1 y2 y3

былай жазуға болады.

(4.5)

(4.6)

Жазықтықтағы түзулердiң түрлi теңдеулерiн қарастырайық:
1) Түзудiң жалпы теңдеуi.
Жазықтықтағы x және y-ке қатысты бiрiншi дәрежелi мына теңдеу
Ax By C 0	(4.7)

51

түзудiң жалпы теңдеуi деп аталады. Мұндағы					A, B және C тұрақты
коэффициенттер және A2 B2 0.
	Түзудiң жалпы теңдеуiнiң дербес жағдайларын зерттейік.
1.	Егер C 0; A 0; B 0			болса, онда Ax By 0	түзуi координаталардың
	бас нүктесi арқылы өтедi.
2.	Егер A 0; B 0; C 0			болса, онда By C 0	немесе	y b	мұндағы
	b	C	түзуi Ox өсiне параллель болады.
		B		болса, онда Ax C 0
3.	Егер B 0; A 0; C 0				немесе	x a	мұндағы

a C түзуi Oy өсiне параллель болады.

A

4.Егер B C 0; A 0 болса, онда Ax 0 немесе x 0 түзуi Oy өсiмен беттеседi.

5.Егер A C 0; B 0 болса, онда By 0 немесе y 0 түзуi Ox өсiмен беттеседi.

2) Бұрыштық коэффициентпен берiлген түзудiң теңдеуi.

Егер түзудiң жалпы теңдеуiнде B 0 болса, онда оны y-ке қатысты

шешiп,
y kx b			(4.8)
түрiндегi теңдеудi аламыз, мұндағы k	A	,	b	C	.
	B			B

(4.8) теңдеуі бұрыштық коэффициентпен берiлген түзу теңдеуi деп аталады. Бұрыштық коэффициент k tg , мұндағы түзудiң Ox өсiнiң оң бағытымен жасайтын бұрышы (оң бағыттағы бұрыш Ox өсiнен сағат тiлiне қарсы бағытта алынады). Ал бос мүше b түзудiң Oy өсiмен қиылысу

	нүктесiнiң ординатасы болып табылады.
	3) Кесiндiдегi түзудiң теңдеуi.					С 0
	Егер түзудiң жалпы теңдеуiнде								болса, онда оның барлық
	мүшелерiн C-ға бөлiп,
		x		y	1				(4.9)
		a b				C				C
	түрiндегi теңдеудi аламыз, мұндағы a						,	b			.
						A				B
	(4.9) теңдеуi кесiндiдегi түзу теңдеуi деп аталады. Теңдеудегi a түзудiң
	Ox өсiмен қиылысу нүктесiнiң абсциссасы,							ал b түзудiң Oy өсiмен қиылысу
	нүктесiнiң ординатасы. Сондықтан a					және				b координат өстерiндегi
	кесiндiлерi деп аталады.
	4) Түзудiң нормаль теңдеуi.

Егер түзудiң Ax By C 0 жалпы теңдеуiнің екi жағын нормальдаушы

көбейткiш деп аталатын		1		санына, радикал алдындағы
		A2 B2

52