Оглавление

1.Вектор. Основные свойства. 3

2.Уравнения прямых и кривых на плоскости 5

3. Плоскость в пространстве 12

4.1.Матрицы. Операции над матрицами 13

4.2. Определители 15

4.3. Ранг матрицы 19

4.4. Обратная матрица 21

5.1. Критерий совместности Кронекера-Капелли 23

5.2. Метод Гаусса 25

5.3. Формулы Крамера 26

5.4. Матричный метод 28

5.5. Системы линейных уравнений общего вида 29

6.1. Предел последовательности и функции. Теоремы о пределах 34

7.1. Производная, правила и формулы дифференцирования 41

7.3. Экстремум функции 45

7.4. Раскрытие неопределенностей. Правило Лопиталя 46

7.5 Частные производные. Метод наименьших квадратов. 47

8.1. Основные методы интегрирования 52

9.1. Вероятность и риск, пространство элементарных событий 60

9.2. Независимость событий. Последовательные события и слепой случай. Теорема умножения вероятностей. "Дерево вероятностей" 63

9.3. Статистическое (частотное) определение вероятности. Теорема сложения вероятностей 67

9.4. Формула полной вероятности 69

9.5. Последовательтность испытаний (схема Бернулли) 71

10.1. Среднее арифметическое, мода и медиана. Среднее квадратическое отклонение 73

10.2. Нормальное распределение и его свойства 77

10.3. Выборки и доверительные интервалы 81

10.4. Центральная предельная теорема. Систематические изменения или случайность 84

10.5. Введение в корреляционный анализ. Основы регрессионного анализа 90

1.Вектор. Основные свойства.

Определение. Вектор – Упорядоченную совокупностьn вещественных чисел называют n-мерным вектором, а числа- компонентами,или координатами,вектора.

Пример 1.1. Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент.

Обозначения. Векторы обозначают жирными строчными буквами или буквами с чертой или стрелкой наверху, например, a или a. Два вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны.

Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1)  (2, 3, 5, 0, 1).

Операции над векторами. Произведением вектора на действительное число называется вектор

Суммой векторов иназывается вектор.

Пространство векторов. N-мерное векторное пространство Rⁿ определяется как множество всех n-мерных векторов, для которых определены операции умножения на действительные числа и сложение.

Линейная независимость. Система n-мерных векторов называется линейно зависимой, если найдутся такие числа , из которых хотя бы одно отлично от нуля, что выполняется равенство; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все . Геометрический смысл линейной зависимости векторов вR³, интерпретируемых как направленные отрезки, поясняют следующие теоремы.

Теорема 1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

Теорема 2. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

Теорема 3. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

Левая и правая тройки векторов. Тройка некомпланарных векторов называется правой, если наблюдателю из их общего начала обход концов векторов в указанном порядке кажется совершающимся по часовой стрелке. B противном случае - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.

Базис и координаты. Тройка некомпланарных векторов в R³ называется базисом, а сами векторы - базисными. Любой вектор может быть единственным образом разложен по базисным векторам, то есть представлен в виде

(1.1)

числа в разложении (1.1) называютсякоординатами вектора в базисеи обозначаются .

Ортонормированный базис. Если векторы попарно перпендикулярны и длина каждого из них равна единице, то базис называетсяортонормированным, а координаты -прямоугольными. Базисные векторы ортонормированного базиса будем обозначать .

Будем предполагать, что в пространстве R³ выбрана правая система декартовых прямоугольных координат .

Пример 1.2. Найдите угол между векторами и, где и - единичные векторы и угол между иравен 120^о.

Решение. Имеем: ,,

, значит

, значит

Окончательно имеем: .

Пример 1.3. Зная векторы и, вычислите площадь треугольника ABC.

Решение. Обозначая площадь треугольника ABC через S, получим:

. Тогда ,,

Пример 1.4. Даны два вектораи. Найдите единичный вектор, ортогональный векторам ии направленный так, чтобы упорядоченная тройка векторов,,была правой.

Решение. Обозначим координаты вектора относительно данного правого ортонормированного базиса через.

Поскольку ,, то , . По условию задачи требуется, чтобыи.

Имеем систему уравнений для нахождения:

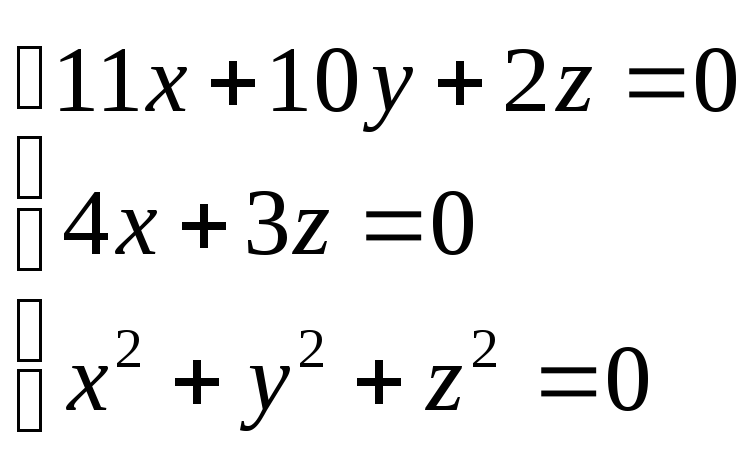
Из первого и второго уравнений системы получим ,. Подставляяив третье уравнение, будем иметь:, откуда. Используя условие, получим неравенство

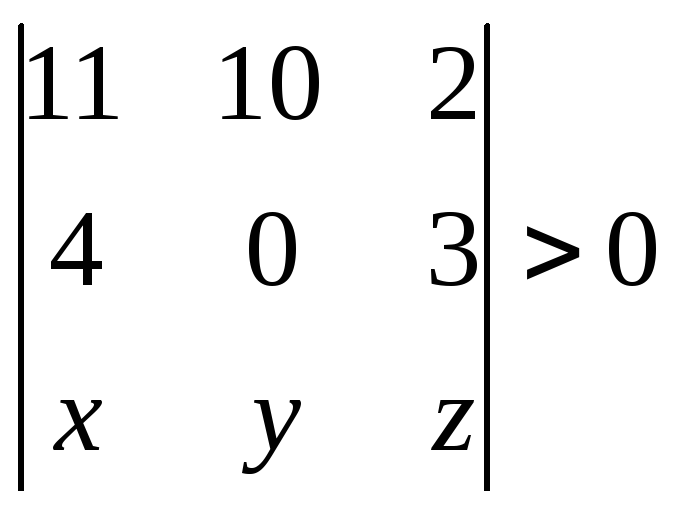или

С учетом выражений для иперепишем полученное неравенство в виде:, откуда следует, что. Итак,,,.