
- •Матрицы. Операции над матрицами. Матрицы.
- •Виды матриц.
- •Операции над матрицами.
- •Определители квадратных матриц
- •Обратная матрица.
- •Системы линейных уравнений.
- •Метод обратной матрицы.
- •Метод Крамера.
- •Метод Гаусса.
- •Производная.
- •Правила дифференцирования.
- •Производные сложной и обратной функции.
- •Интегрирование.
- •Свойства неопределенного интеграла.
- •Метод замены переменной.
- •Метод интегрирования по частям.
- •Задания для контрольных работ (6 заданий по 25 вариантов)
- •Задание №1
- •Задание №2
Матрицы. Операции над матрицами. Матрицы.
Определение.
Матрицей размера
![]() называется таблица чисел, состоящая из
называется таблица чисел, состоящая из![]() строк и
строк и![]() столбцов. Числа, составляющие матрицу,
называются элементами матрицы.
столбцов. Числа, составляющие матрицу,
называются элементами матрицы.
Матрицы обозначаются
прописными буквами латинского алфавита
(например А,
В, С), а
элементы матрицы – строчными буквами
с двойной индексацией:
![]() ,
где
,
где![]() – номер строки,
– номер строки,![]() – номер столбца.
– номер столбца.
Например, матрица
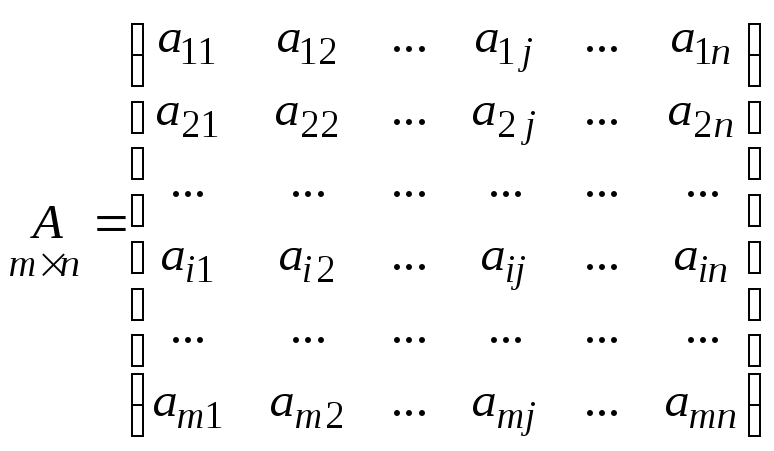 ,
,
или в сокращенной
записи
![]() ,
где
,
где![]() ;
;![]() .
.
Виды матриц.
Матрица, состоящая
из одной строки, называется матрицей
(вектором)–строкой,
а из одного столбца – матрицей
(вектором)–столбцом:
![]() – матрица–строка;
– матрица–строка;
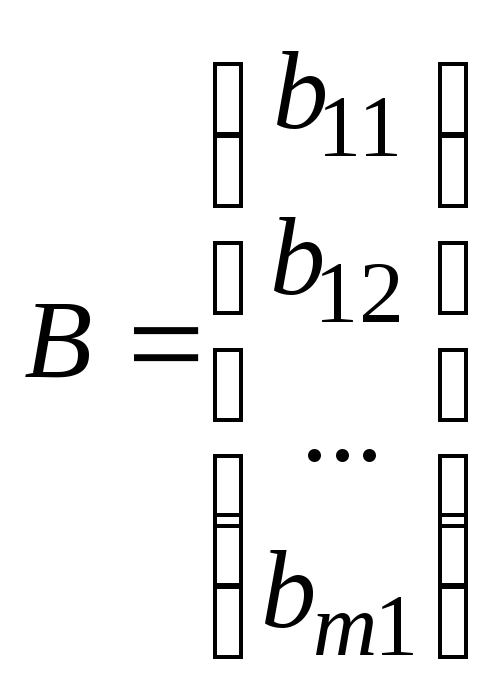 –матрица–столбец.
–матрица–столбец.
Матрица называется
квадратной
![]() -го
порядка, если число ее строк равно числу
столбцов и равно
-го
порядка, если число ее строк равно числу
столбцов и равно
![]() .
Например,
.
Например,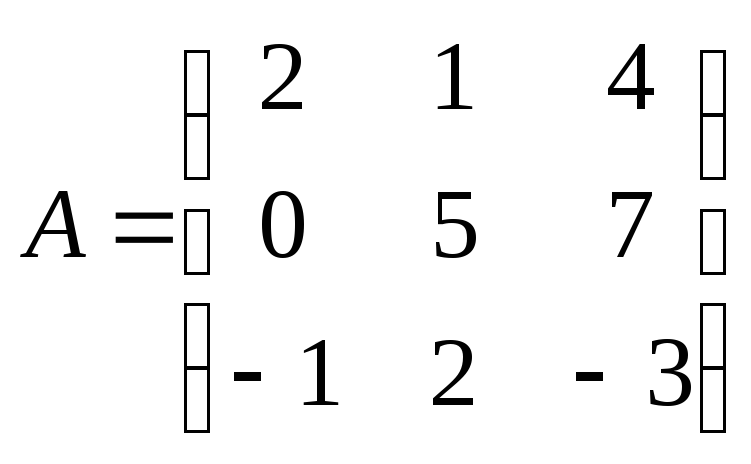 – квадратная матрица третьего порядка.
– квадратная матрица третьего порядка.
Элементы матрицы
![]() ,
у которых номер строки равен номеру
столбца
,
у которых номер строки равен номеру
столбца![]() ,
называютсядиагональными
и образуют главную
диагональ
матрицы.
,
называютсядиагональными
и образуют главную
диагональ
матрицы.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
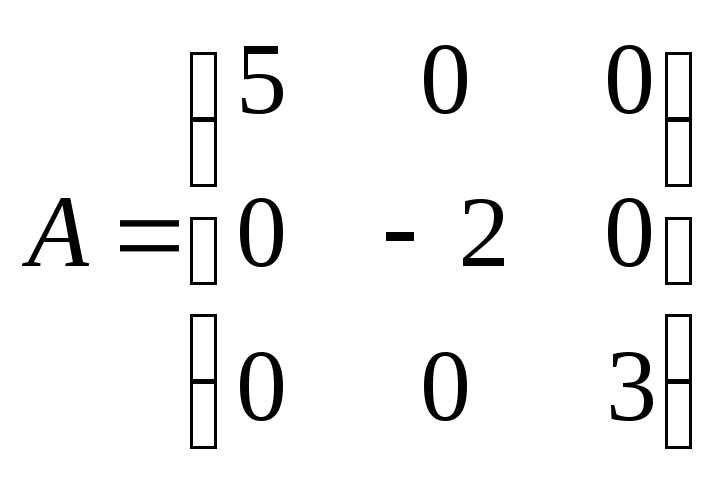 –диагональная
матрица третьего порядка.
–диагональная
матрица третьего порядка.
Если у диагональной
матрицы
![]() -го
порядка все диагональные элементы равны
единице, то матрица называетсяединичной
матрицей
-го
порядка все диагональные элементы равны
единице, то матрица называетсяединичной
матрицей
![]() -го
порядка и она обозначается буквой
-го
порядка и она обозначается буквой![]() .
Например,
.
Например,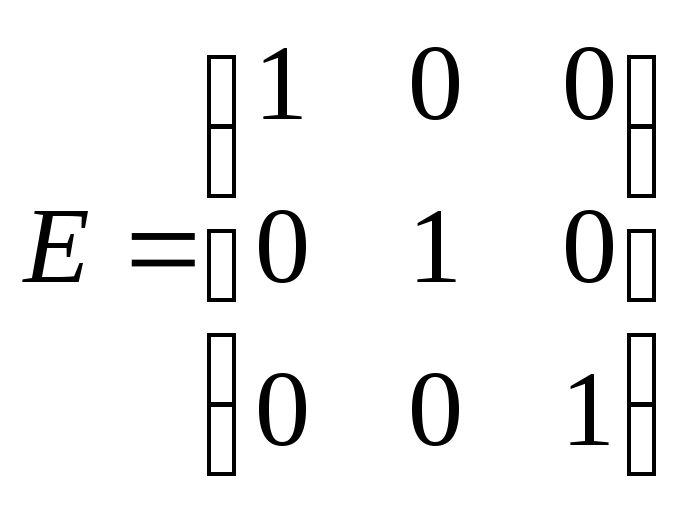 – единичная матрица третьего порядка.
– единичная матрица третьего порядка.
Операции над матрицами.
Умножение матрицы на число. Произведением матрицы
 на число
на число называется
матрица
называется
матрица
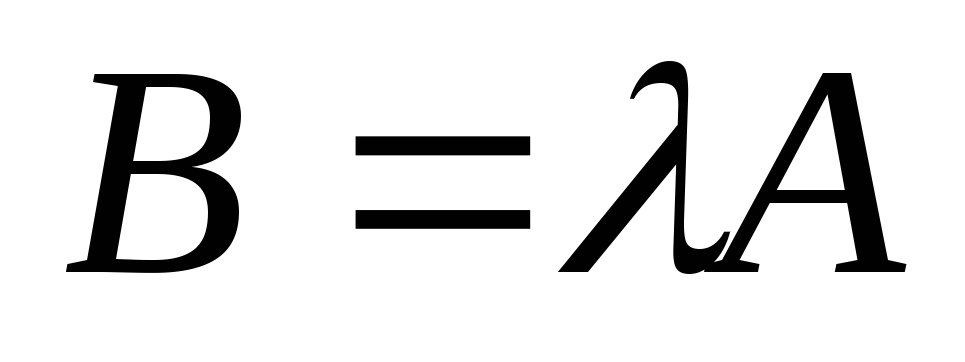 ,
элементы которой
,
элементы которой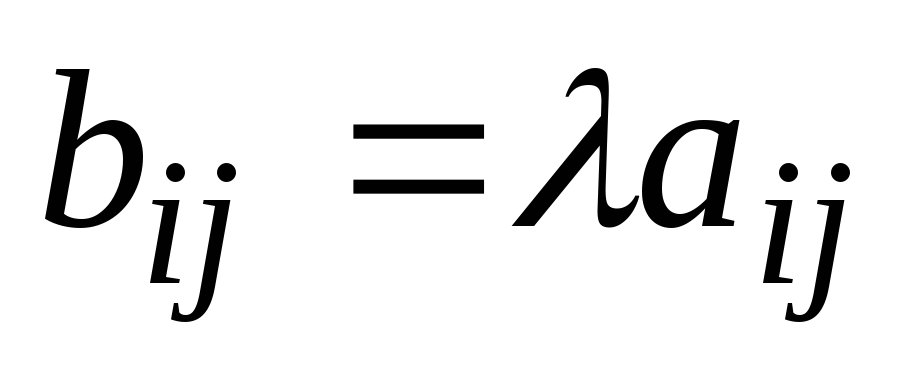 для
для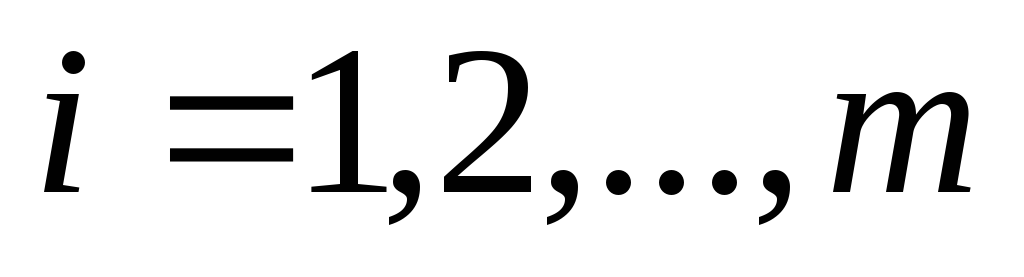 ;
;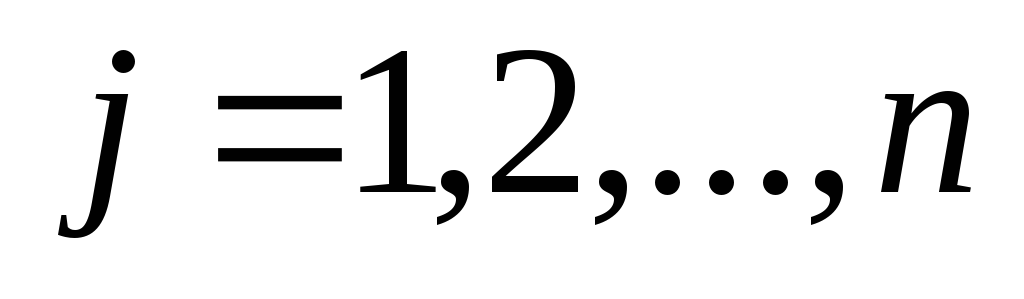 .
.
Например, если
![]() ,
то
,
то![]() .
.
Сложение матриц. Суммой двух матриц
 и
и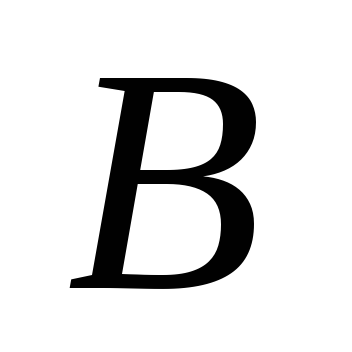 одинакового размера
одинакового размера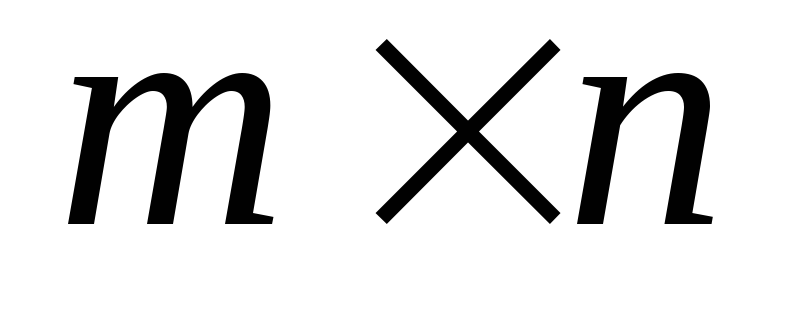 называется матрица
называется матрица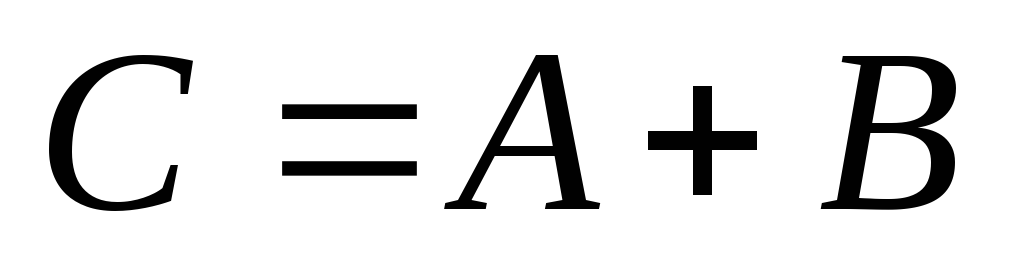 ,
элементы которой
,
элементы которой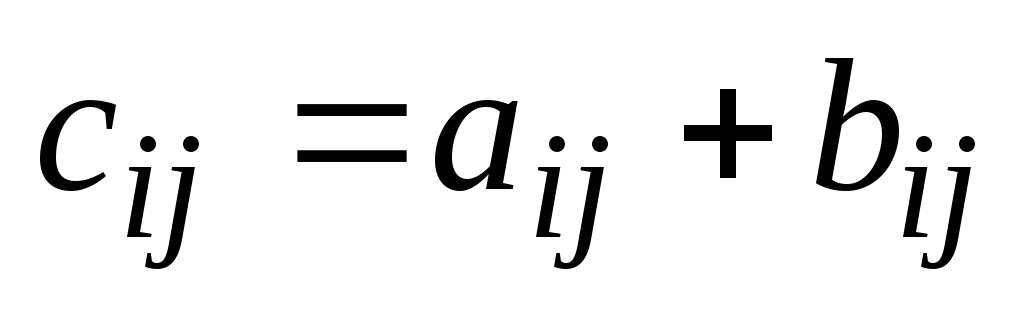 для
для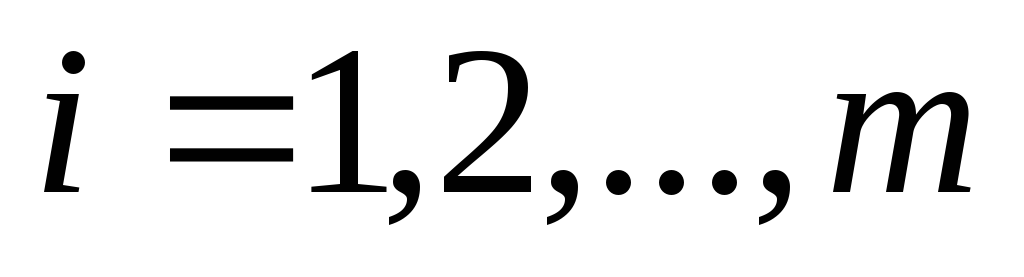 ;
;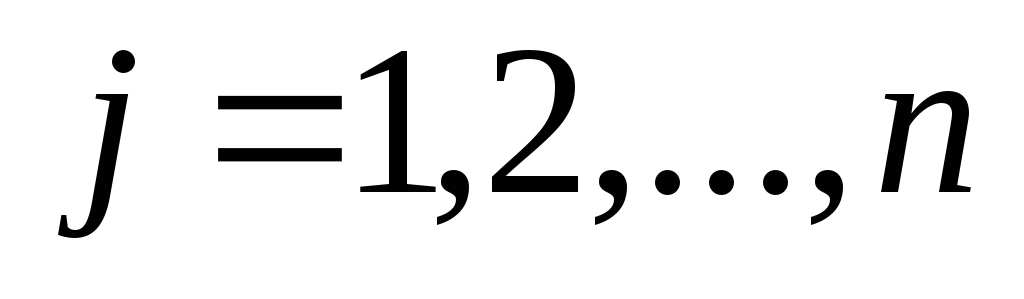 (то есть матрицы складываются поэлементно).
(то есть матрицы складываются поэлементно).
Например:
![]() ,
,![]() ,
,![]() .
.
Умножение матриц. Умножение матрицы
 на матрицу
на матрицу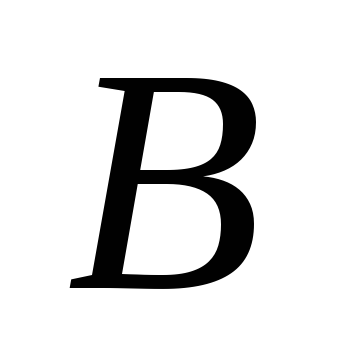 определено, когдачисло
столбцов матрицы
определено, когдачисло
столбцов матрицы
 равно числу строк матрицы
равно числу строк матрицы
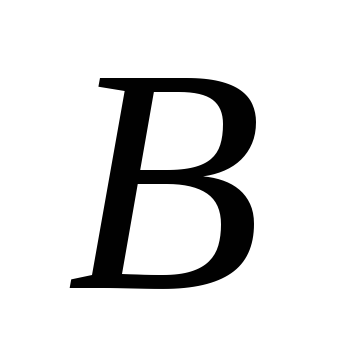 .
Тогда произведением матриц
.
Тогда произведением матриц называется матрица
называется матрица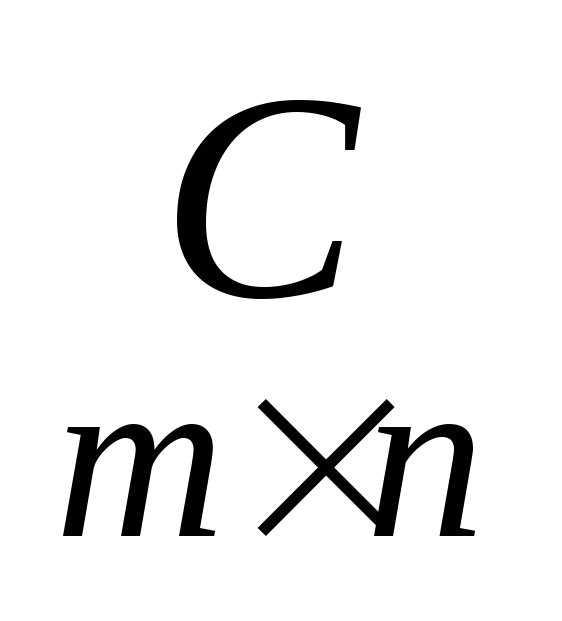 ,
каждый элемент которой
,
каждый элемент которой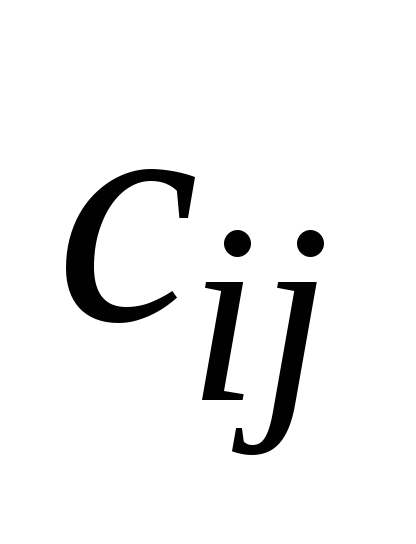 равен сумме произведений элементов
равен сумме произведений элементов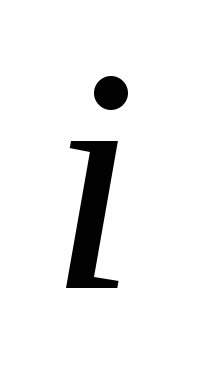 -ой
строки матрицы
-ой
строки матрицы на соответствующие элементы
на соответствующие элементы -го
столбца матрицы
-го
столбца матрицы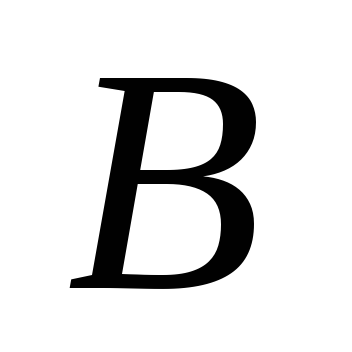 :
:
![]()
Пример. Вычислить
произведение матриц
![]() ,где
,где
![]() ;
;
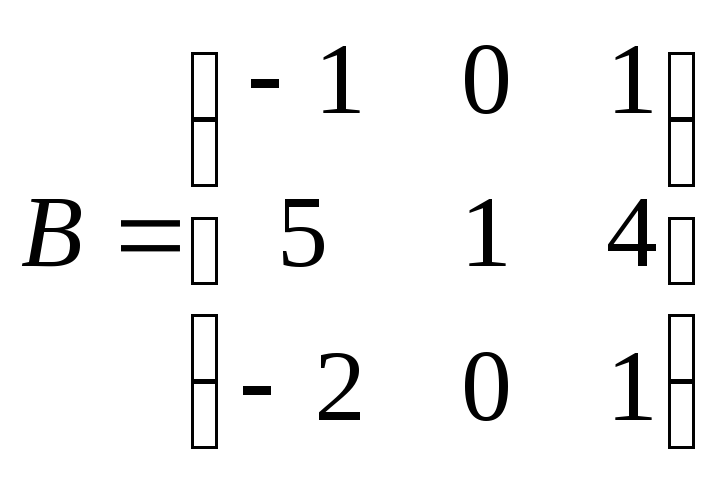 .
.
Найдем размер
матрицы-произведения (если умножение
матриц возможно):
![]() .
Вычислим элементы матрицы
.
Вычислим элементы матрицы![]() .
Элемент
.
Элемент![]() получается при умножении
получается при умножении![]() -ой
строки матрицы
-ой
строки матрицы![]() на
на![]() -ый
столбец матрицы
-ый
столбец матрицы![]() .
.
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Получаем
![]() .
.
Транспонирование матрицы – переход от матрицы
 к матрице
к матрице ,
в которой строки и столбцы поменялись
местами с сохранением порядка. Матрица
,
в которой строки и столбцы поменялись
местами с сохранением порядка. Матрица называется транспонированной относительно
матрицы
называется транспонированной относительно
матрицы .
.
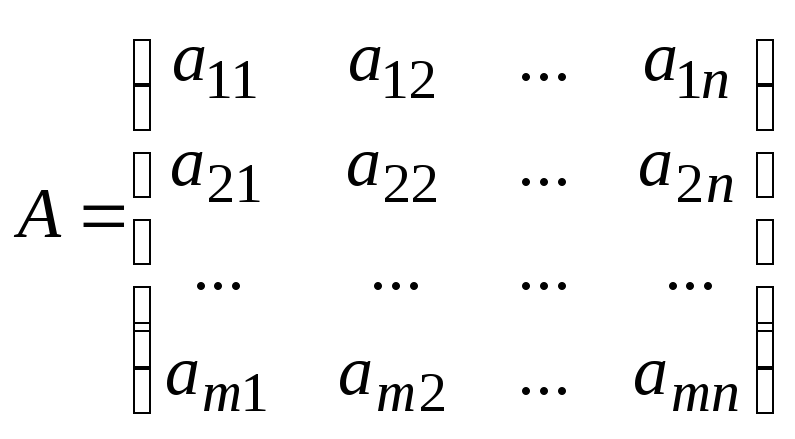 ,
,
 .
.
Из определения
следует, что если матрица имеет размер
![]() ,
то транспонированная матрица
,
то транспонированная матрица![]() имеет размер
имеет размер![]() .
.
Например:
![]() ;
;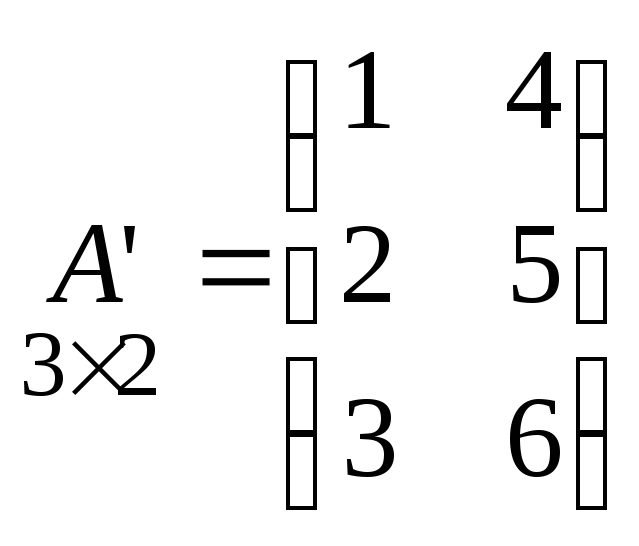 .
.
Определители квадратных матриц
Определитель – это число, характеризующее квадратную матрицу.
Определитель
матрицы
![]() обозначается
обозначается![]() или
или![]() .
.
Определителем
матрицы первого порядка
![]() ,
илиопределителем
первого порядка,
называется элемент
,
илиопределителем
первого порядка,
называется элемент
![]() :
:
![]() .
Например, пусть
.
Например, пусть
![]() ,
тогда
,
тогда![]() .
.
Определителем
матрицы второго порядка
![]() ,
илиопределителем
второго порядка,
называется число, которое вычисляется
по формуле:
,
илиопределителем
второго порядка,
называется число, которое вычисляется
по формуле:
![]() .
.
Произведения
![]() и
и![]() называютсячленами
определителя
второго порядка. Например, пусть
называютсячленами
определителя
второго порядка. Например, пусть
![]() ,
тогда
,
тогда![]() .
.
Пусть дана квадратная матрица третьего порядка:
 .
.
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
![]()
Рис. 1.
Это число представляет собой алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строка и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу, легко запомнить, пользуясь схемой (рис.1.), которая называется правилом треугольников или правилом Сарруса.
Для вычисления определителей более высоких порядков потребуются некоторые дополнительные понятия.
Пусть дана квадратная
матрица
![]() n-го
порядка.
n-го
порядка.
Минором
![]() элемента
элемента![]() матрицы n-го
порядка называется определитель матрицы
(n–1)-го
порядка, полученной из матрицы
матрицы n-го
порядка называется определитель матрицы
(n–1)-го
порядка, полученной из матрицы
![]() вычеркиванием
вычеркиванием![]() -ой
строки и
-ой
строки и![]() -го
столбца.
-го
столбца.
Например, минором
элемента
![]() матрицы
матрицы![]() третьего порядка будет:
третьего порядка будет:
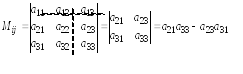
Алгебраическим
дополнением
![]() элемента
элемента
![]() матрицы n-го
порядка называется его минор, взятый
со знаком
матрицы n-го
порядка называется его минор, взятый
со знаком
![]() :
:![]() ,
т.е. алгебраическое дополнение совпадает
с минором, когда сумма номеров строки
и столбца (i+j)
– четное число, и отличается от минора
знаком, когда (i+j)
– нечетное число. Например,
,
т.е. алгебраическое дополнение совпадает
с минором, когда сумма номеров строки
и столбца (i+j)
– четное число, и отличается от минора
знаком, когда (i+j)
– нечетное число. Например,
![]() ;
;![]() .
.
Для вычисления определителей квадратных матриц выше третьего порядка пользуются теоремой Лапласа.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
![]()
(разложение по
элементам i-й
строки;
![]() );
);
![]()
(разложение по
элементам j-го
столбца;
![]() );
);
По свойствам определителей, определитель матрицы не изменится, если к элементам любой строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число. Это свойство определителей и теорема Лапласа позволяют существенно упростить вычисление определителей высоких порядков. При вычислении определителей нужно преобразовать исходную матрицу так, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример. Вычислить определитель четвертого порядка:
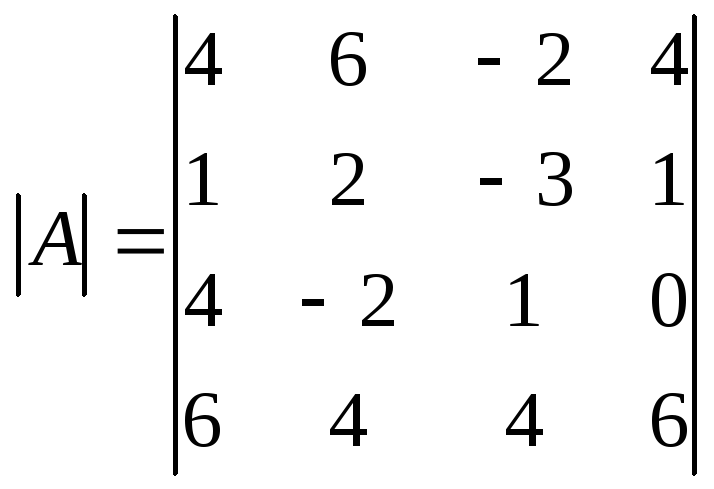 .
.
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем
 .
.
Полученный определитель третьего порядка можно вычислить по правилу треугольников или с помощью теоремы Лапласа, однако, можно продолжить упрощение матрицы. "Обнулим" в матрице третьего порядка элементы 2-ой строки (кроме одного). Для этого элементы третьего столбца матрицы, предварительно умножив на (-13) и на 4, сложим с элементами 1-го и 2-го столбцов соответственно:
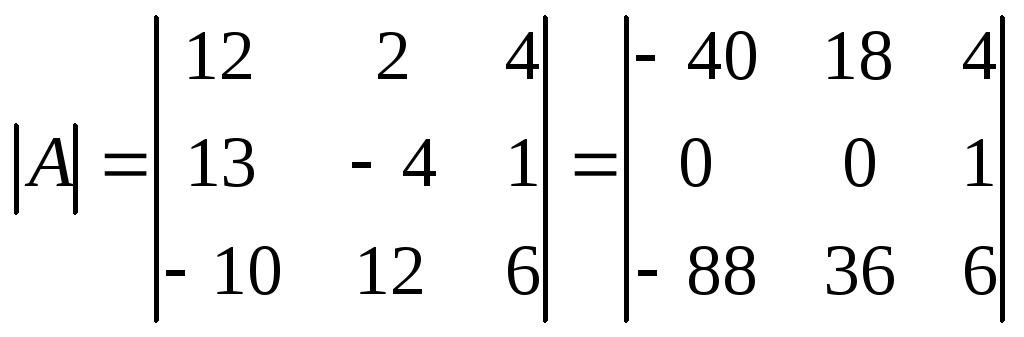 .
.
Раскладывая по элементам второй строки и вынося общие множители, получаем:
![]() .
.
