FETsk / k_Bulgakov

Н.А. БУЛГАКОВ, И.А. ОСИПОВА

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ ПО МАТЕМАТИКЕ И ФИЗИКЕ

ШКОЛЬНАЯ МАТЕМАТИКА

ВЫСШАЯ МАТЕМАТИКА

ФИЗИКА

• ИЗДАТЕЛЬСТВО ТГТУ •

Министерство образования и науки Российской Федерации

ГОУ ВПО«Тамбовский государственный технический университет»

Н.А. БУЛГАКОВ, И.А. ОСИПОВА

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ ПО МАТЕМАТИКЕ И ФИЗИКЕ

ШКОЛЬНАЯ МАТЕМАТИКА

ВЫСШАЯ МАТЕМАТИКА

ФИЗИКА

СПРАВОЧНОЕ ПОСОБИЕ

Тамбов Издательство ТГТУ

2007

УДК 531(075)

ББК В3я73

Б907

Р е ц е н з е н т

Доктор технических наук, профессор кафедры «Автоматизированные системы и приборы» ТГТУ, заслуженный изобретатель России

М.М. Мордасов

Б907 Булгаков, Н.А.

Основные законы и формулы по математике и физике: справ. пособие / Н.А. Булгаков, И.А. Осипова. – Тамбов : Изд-во Тамб. гос. техн. ун-та, 2007. – 136 с. – 500 экз. – ISBN 978-5-8265-0618-9.

Представлены в сжатой форме основные законы и формулы по всему курсу физики, а также по школьной и высшей математике, знание которых необходимо для решения задач и осмысления физической сущности явлений.

Основное назначение – помочь быстро найти или восстановить в памяти необходимые законы и формулы. Используется современная терминология и обозначения.

Привлекателен в качестве справочного материала при подготовке к семинарским занятиям и экзаменам. Помимо студентов вузов может быть полезен инженернотехническим работникам и учащимся колледжей и школ.

УДК 531(075)

ББК В3я73

ISBN 978-5-8265-0618-9 ГОУ ВПО «Тамбовский государственный технический университет» (ТГТУ), 2007

Справочное издание

БУЛГАКОВ Николай Александрович, ОСИПОВА Ирина Анатольевна

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ ПО МАТЕМАТИКЕ И ФИЗИКЕ

ШКОЛЬНАЯ МАТЕМАТИКА ВЫСШАЯ МАТЕМАТИКА

ФИЗИКА

Справочное пособие

Редактор Е.С. Мордасова Инженер по компьютерному макетированию Т.А. Сынкова

Подписано в печать 8.08.2007.

Формат 60 × 84 / 32. 5,9 усл. печ. л.

Тираж 500 экз. Заказ № 501

Издательско-полиграфический центр Тамбовского государственного технического университета,

392000, Тамбов, Советская 106, к. 14

ШКОЛЬНАЯ МАТЕМАТИКА

● Числовые неравенства:

Если a > b , то b < a .

Если a > b и b > c , то a > c .

Если a > b , то a +c > b +c .

Если a > b и c > 0 , то ac > bc .

Если a > b и c < 0 , то ac < bc .

Если a > b и c > d , то a +c > b + d .

Если a > 0 ,

b > 0 , c > 0 ,

d > 0 , причем a > b и c > d , то ac > bd .

Если a > b > 0 и n – натуральное число, то an > bn .

● Разложение на множители:

a2 −b2 = (a −b)(a +b);

a2 ± 2ab +b2 = (a ±b)2 ;

a3 ±b3 = (a ±b)(a2 mab +b2 );

a3 ±3a2b +3ab2 ±b3 = (a ±b)3 ;

ax2 +bx + c = a(x − x )(x − x ),

1

2

где x и x

2

– корни уравнения ax2 +bx +c = 0 .

1

● Квадратное уравнение ax2 +bx + c = 0 :

x

=

−b ±

D

=

−b ± b2 −4ac

– формула корней квадратного уравнения.

1,2

2a

2a

Теорема Виета:

x + x

= − b ,

x x

2

= c .

1

2

a

1

a

● Арифметическая прогрессия:

a1 , a2 , ..., an , ... – членыарифметическойпрогрессии;

d – разность арифметической прогрессии;

an+1 = an + d – определение арифметической прогрессии;

an = a1 + d (n −1)

– формула n-го члена;

an

= an−1 + an+1

– характеристическое свойство;

2

Sn = a1 + an n = 2a1 + d (n −1)n – формула суммы n первых членов.

2

2

● Геометрическая прогрессия:

a1 , a2 , ..., an , ... – членыгеометрическойпрогрессии;

q – знаменатель геометрической прогрессии;

bn+1 = b q, b ≠ 0, q ≠ 0 – определение геометрической прогрессии;

b

= b qn−1

– формула n-го члена;

n

1

b2

= b

b

– характеристическое свойство;

n

n−1 n+1

(qn −1)

Sn

=

b q −b

=

b

– формула суммы n первых членов;

n

1

1

q −

1

q −1

S =

1

b1

– формула суммы бесконечной геометрической прогрессии при q <1 .

− q

ТРИГОНОМЕТРИЯ

● Свойства тригонометрических функций:

sin(−x)= −sin x ;

sin(x + 2πk )= sin x ;

cos(−x)= cos x ; cos(x + 2πk )= cos x ;

tg (−x)= −tg x ;

tg (x + πk )= tg x ;

ctg(−x)= −ctg x ;

ctg(x + πk )= ctg x ,

где k – любое целое число.

● Таблица значений тригонометрических функций некоторых углов

Аргумент α

Функция

0

π

π

π

π

π

3π

6

4

3

2

2

sin α

0

1

2

3

1

0

–1

2

2

2

cos α

1

3

2

1

0

–1

0

2

2

2

tg α

0

3

1

3

–

0

–

3

ctg α

–

3

1

3

0

–

0

3

П р и м е ч а н и е .

Связь между

градусной

и радианной

мерами измерения угла: 1° = π / 180 рад.

● Формулы, связывающие тригонометрические функции одного и того же аргумента:

sin2 α +cos2 α =1;

tg α = sin α

;

ctg

α =

cosα

;

cosα

sin α

1+ tg2 α =

1

;

1+ ctg2 α =

1

.

cos2

α

sin2 α

● Формулы двойного угла:

sin 2α = 2sin αcosα =

2tg α

;

+ tg2α

1

cos2α = cos

2

α −sin

2

α =1− 2sin

2

α =

1− tg2 α

;

1+ tg2 α

tg 2α =

2 tg α

;

ctg 2α =

ctg2 α −1

.

− tg2α

2ctg α

1

● Формулы тройного угла:

sin 3α = 3sin α −4sin3 α;

cos3α = 4cos3 α −3cosα.

● Формулы понижения степени:

sin2 α = 1−cos2α ;

cos2 α =

1+cos2α .

● Формулы сложения и вычитания аргументов:

2

2

sin(α ±β)= sin αcosβ±cosαsinβ ;

cos(α ±β)= cosαcosβmsin αsinβ ;

tg(α ±β)=

tg α ± tgβ

.

1m tg αtgβ

● Формулы сложения и вычитания тригонометрических функций:

sin α +sin β = 2sin	α +β cos		α −β		;
		2		2
sin α −sin β = 2sin	α −β cos		α +β		;
		2		2
cos α + cosβ = 2 cos		α +β cos		α −β	;
		2		2
cos α −cosβ = −2sin		α +β sin		α −β ;
		2		2

tg α m tg β = sin (α ±β) . cos αcosβ

● Формулы преобразования произведения тригонометрических функций в сумму и разность:

	sin αsinβ =	1			(cos(α −β)− cos(α +β)) ;
		2
	cosαcosβ =		1		(cos(α −β)+ cos(α +β)) ;
		2
	sin αcosβ =		1		(sin(α −β)+ sin(α +β)).
		2

● Знаки тригонометрических функций по четвертям

	Функция			Четверть
		I	II		III	IV
	sin	+	+		–	–
	cos	+	–		–	+
	tg	+	–		+	–
	ctg	+	–		+	–

● Формулы приведения

Аргумент t

Функция -

π

− α

π

+ α

π−α

π+α

3π

−α

3π

+ α

2π − α

2

2

2

2

sin t

cos α

cos α

sin α

– sin α

– cos α

– cos α

– sin α

cos t

sin α

– sin α

– cos α

– cos α

– sin α

sin α

cos α

tg t

ctg α

– ctg α

– tg α

tg α

ctg α

– ctg α

– tg α

ctg t

tg α

– tg α

– ctg α

ctg α

tg α

– tg α

– ctg α

● Решение простейших тригонометрических уравнений:

sin x = a ,

a

≤1,

x = (−1)n arcsin a + πn ;

cos x = a,

a

≤1,

x = ±arccosa + 2πn ;

tg x = a, x = arctga + πn ;

ctg x = a, x = arcctga + πn ,

● Обратные тригонометрические функции:

n – целое число.

−

π

≤ arcsin x ≤

π

, 0 ≤ arccos x ≤ π ;

2

2

−

π

< arctg x <

π

, 0 < arcctg x < π ;

2

2

arcsin(−x)= −arcsin x;

arccos(−x)= π−arccos x ;

arctg(−x)= −arctg x;

arcctg(−x)= π−arcctg x .

МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКАХ

Обозначения: a, b, c – длины сторон ∆ ABC

ностей.

●Теорема синусов. В любом треугольнике

●Теорема косинусов. В любом треугольнике

●Формулы площади любого треугольника:

S = ah2a = bh2b = ch2c , S = 12 absin γ, S = pr, S =

S = p(p − a)(p − b)(p − c) – формула Герона.

, h – высота, p = a+2b+c – полупериметр, S – площадь, R и r – радиусы описанной и вписанной окруж- sinaα = sinb β = sinc γ .

a2 = b2 + c2 − 2bc cosα .

abc

4R

,

ГРАФИКИ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

● Линейная функция у = ах + b.

Графиком этой функции является прямая линия. Функция возрастает при а > 0 и убывает при а < 0. Оси координат пересекаются прямой в точках A(– b/a; 0) и B(0; b). В случае b = 0 получаем прямую пропорциональность у = ах. График функции проходит через начало координат.

● Квадратичная функция у = ах2 + bх + с.

Графиком функции является парабола с осью симметрии, параллельной оси ординат. При а > 0 ветви параболы направлены вверх, при а < 0 – вниз.

− b

4ac −b

2

Ось ординат пересекается кривой в точке В(0; с). Вершина параболы С имеет координаты

,

. Абсциссы x1, x2

точек пересечения параболы

2a

4a

с осью Ох определяют по формуле х1,2 =

− b ±

b2 − 4ac

. Величины х1

2

2a

и х2 являются корнями квадратного уравнения ax + bx + c = 0 в том случае, когда

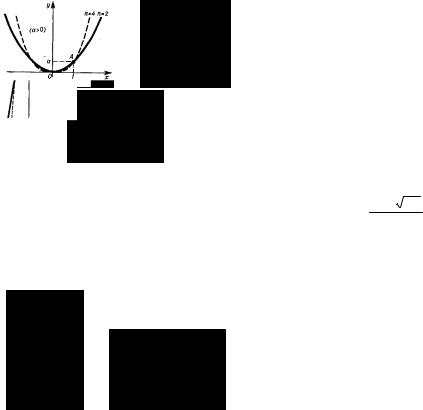
оно имеет решения на множестве действительных чисел. ● Многочлен третьей степени y = ax3 + bx2 + cx + d.

Графиком функции является кубическая парабола. Поведение функции зависит от знаков а и ∆ = 3ас – b2. В случае ∆ ≥ 0 функция возрастает при а > 0 и убывает при а < 0. Если же ∆ < 0, то функция имеет одну точку максимума и одну точку минимума. Кубическая парабола имеет одну точку пере-

гиба K. Ось ординат пересекается кривой в точке В(0; d). Абсциссы точек максимума и минимума x4 и х5 определяют по формуле							−b ± −∆	. Абсцисса
							3a
			b		∆
точки перегиба х6	равна	−		. Касательная к графику в точке перегиба наклонена к оси Ох под углом α таким, что tg α =		.
					3a
			3a

● Степенная функция у = ахn (n > 1 – целое)

Графиком функции является парабола n-го порядка, которая проходит через точки О(0; 0) и А(1; а) и касается оси Ох в начале координат. При n четном график функции симметричен относительно оси Оу и в начале координат имеет минимум при а > 0 и максимум при а < 0. При n нечетном график функции симметричен относительно начала координат, которое является точкой перегиба графика.

ВЫСШАЯ МАТЕМАТИКА

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

●●●●●●

d =

(x

− x )2

+(y

2

− y )2

– расстояние между точками M

(x ;

y )

и M

2

(x ; y

2

) .

2

1

1

1

1

1

2

●

x =

x1 + λx2

,

y =

y1 + λy2

– координаты точки, делящей отрезок с концами M

(x ; y )

и M

2

(x ; y

2

)

в отношении λ =

M

M

:

MM

2

.

1+ λ

1+ λ

1

1

1

2

1

A2 + B2 ≠ 0) .

●

Ax + By +C = 0 – общее уравнение прямой ( A, B, C – любые вещественные числа,

●

y = kx +b – уравнение прямой с угловым коэффициентом k ( b – величина отрезка, отсекаемого прямой по оси Oy ).

●

y − y1 = k (x − x1 )

– уравнение прямой с угловым коэффициентом k , проходящей через точку M1(x1 ;

y1 ) .

●

y − y1

=

x − x1

– уравнение прямой, проходящей через точки M

(x ;

y )

и M

2

(x ; y

2

) .

y2 − y1

x2 − x1

1

1

1

2

●

x

+

y

=1 – уравнение прямой в отрезках ( a, b – величиныотрезков, отсекаемыхпрямойнаосях Ox и Oy ).

a

b

●

d =

Ax0 + Bx0

+C

– расстояние от точки M0 (x0 ; y0 ) до прямой

Ax + By +C

= 0 .

A2 + B2

●

tg ϕ =

k2 −k1

– формула вычисления одного из углов между прямыми

y = k x +b

и y = k

2

x +b .

1+ k1k2

1

1

2

●

x

2

+

y

2

=1 – каноническое уравнение эллипса ( a, b – полуоси).

a2

b2

●

x

2

−

y

2

=1 – каноническоеуравнениегиперболы.

a2

b2

●

y2 = 2 px, y2 = −2 px – каноническое уравнение параболы с осью симметрии Ox ( p > 0 – параметр).

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

В ПРОСТРАНСТВЕ

X = x2 − x1 , Y = y2 − y1 , Z = z2 − z1 – выражение координат вектора

через координаты точек

A(x1 ; y1 ; z1 ) и B(x2 ; y2 ;

z2 ) .

●

AB

a =

X 2 +Y 2 + Z 2

– выражение длины вектора

={X ; Y ; Z} через его координаты.

●

a

●

d =

(x − x )2

+(y

2

− y )2 +(z

2

− z )2 – расстояние между точками M (x ; y ; z )

и M

2

(x ; y ; z ) .

2

1

1

1

1

1

1

1

2

2

2

=

cosϕ – определение скалярного произведениявекторов a и

(ϕ – уголмеждувекторами).

●

a

b

a

b

b

= X1X2 +Y1Y2 + Z1Z2

выражение скалярного произведения векторов

={X1 ; Y1 ; Z1} и

={X2 ; Y2 ; Z2} через их координаты.

●

a

b

–

a

b

●

cosϕ =

X1X2 +Y1Y2

+ Z1Z2

– выражение угла между векторами.

X 2

+Y 2

2 +Y 2

+ Z

2

X

+ Z 2

1

1

1

2

2

2

●

Ax + By +Cz + D = 0 – общее уравнение плоскости ( A, B, C – любые вещественные числа,

A2 + B2 +C2 ≠ 0 ).

●

d =

Ax0 + By0

+Cz0 + D

– расстояние от точки M0 (x0; y0; z0 ) до плоскости

Ax + By +Cz + D = 0 .

A2 + B2 +C2

●

x − x0

=

y − y0

=

z − z0

– каноническое уравнение прямой с направляющим вектором a ={l ; m; n}, проходящей через точку

M

0

(x ; y ; z

0

).

l

m

n

0

0

●

x = x0 +lt ,

y = y0 + mt ,

z = z0 + nt – параметрические уравнения прямой.

●

x

2

+

y

2

+

z2

=1 – каноническое уравнение эллипсоида ( a, b, c – полуоси).

a2

b2

c2

●

x

2

+

y

2

−

z2

=1 – каноническое уравнение однополосного гиперболоида.

a2

b2

c2

●

x

2

+

y

2

−

z2

= −1 – каноническое уравнение двуполосного гиперболоида.

a2

b2

c2

●

x2

+

y2

= z

– каноническое уравнение эллиптического параболоида (p > 0, q > 0 – параметры).

2 p

2q

●

x2

−

y2

= z

– каноническое уравнение гиперболического параболоида.

2 p

2q

●

x2

+

y2

−

z2

= 0 – каноническое уравнение конуса второго порядка.

a2

b2

c2

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

●

lim sin x =1 – первый замечательный предел.

x→0

x

1 x

●

lim 1+

= e – второй замечательный предел.

x→∞

x

●

f ′(x0 )= lim

f (x0 + ∆x)− f (x0 )

– определение производной функции

y = f (x) в точке x0 .

∆x→0

∆x

●

dy = f ′(x0 )dx – дифференциал функции f (x) в точке x0 .

● Производные простейших элементарных функций:

–

Правила дифференцирования суммы, разности, произведения и частного

1)(u ± v)′ = u′± v′ ;

2)(uv)′ = u′v +uv′ ;

′

′

′

3)

u

=

u v −uv

,

v ≠ 0.

v2

v

– Производная постоянной функции

y = f (x)= C y′ = 0 ,

(Cu)′

= Cu′ .

– Производная степенной функции

′

(x

n ′

n−1

;

(

′

1

1

;

2

)

= nx

x )

= x

=

2

x

1

′

−1

′

1

= (x

)

= −

.

x

2

x

– Производная показательной функции

(ax )′ = ax ln a ;

(ex )′ = ex .

– Производная логарифмической функции

(loga x)′ =

1

;

(ln x)′ =

1

.

xln a

x

● Производные тригонометрических функций:

′

= cos x ;

(arcsin x)′ =

1

;

(sin x)

1− x2

′

= −sin x ;

(arccos x)′ = −

1

;

(cos x)

1− x2

′

1

2

′

1

(tg x) =

= sec

x ;

(arctg x)

=

;

cos2 x

1+ x2

′

1

2

′

1

(ctg x)

= −

= −cosec x ;

(arcctg x)

= −

.

sin2 x

1+ x2

●

y′(t0 ) = f ′(x0 ) ϕ′(t0 )

– правило дифференцирования сложной функции

y = f [ϕ(t)] в точке t0 ; здесь x0 = ϕ(t0 ).

●

ϕ′(y0 )=

1

– правило дифференцирования обратной функции x = ϕ(y)

в точке

y0 = f (x0 ).

f ′(x0 )

(n)

(n)

(n−1)

′

n(n −1)

(n−2)

′′

(n)

●

(uv)

=u

v + nu

v

+

1 2

u

v

+...+

+ uv

– формула Лейбница.

●

f (b)

− f (a)

′

– формула Лагранжа;

c (a, b) .

b

− a

= f (c)

●

f (b)− f (a)

=

f ′(c)

– формула Коши;

c (a, b) .

g (b)− g (a)

g′(c)

● f (x)= f (a)+

f ′(a)

(x

−a)+

f ′′(a)

(x −a)2 +

1!

2!

+...+

f (n) (a)

(x −a)

n

+

f (n+1) (ξ)

(x − a)

n+1

– формула Тейлора;

ξ

(a, x).

n!

(n +1)!

● При a = 0 получаем формулу Маклорена

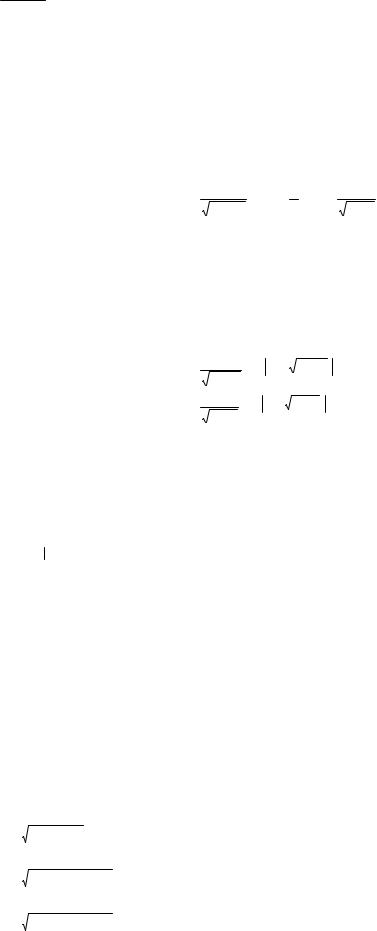
f (x)= f (0)+	f ′(0)	x +	f ′′(0)	x2	+...+	f (n) (0)	x(n) +
	1!		2!
						n!

+f (n+1) (0) x(n+1) .

(n +1)!

●Неопределенный и определенный интегралы

– Табличные интегралы:

∫xαdx =

xα+1

+ C (α ≠ −1);

∫

dx

= ln

x

+ C;

α +1

x

∫axdx =

ax

+ C (0 < a ≠1);

∫exdx = ex + C;

ln a

∫sin xdx = −cos x + C ;

∫cos x dx = sin x +C;

∫

dx

= −ctg x + C ;

∫

dx

= tg x + C;

2

x

2

sin

cos

x

∫

dx

= arcsin x

+ C ;

∫

dx

= arcsin x + C;

a2 − x2

a

1− x2

∫

dx

= arctg x + C ;

∫

dx

=

1

arctg

x

+ C ;

1

+ x

2

a

2

2

a

+ x

a

∫

dx

=

1

x − a

+ C (a ≠ 0);

ln

2

2

2a

x + a

x

− a

∫

dx

=

1

ln

x −1

+ C;

x2 −1

2

x +1

∫

dx

=

1

arctg

x

+C (a ≠ 0);

∫

dx

= arctgx +C;

x

2

+a

2

a

a

x

2

+1

∫

dx

= ln x + x2 ± k + C ;

x2 ± k

∫

dx = ln x + x2 ±1 +C.

x2 ±1

–

′

∫ f (x)dx

x=ϕ(t ) = ∫ f [ϕ(t)]ϕ (t)dt – формула замены переменной в неопределенном интеграле.

b

–

′

ϕ(α) = a , ϕ(β) = b .

∫ f (x)dx = ∫ f [ϕ(t)]ϕ (t)dt – формула замены переменной в определенном интеграле;

a

–

∫u(x)v′(x)dx =u(x)v(x)−∫v(x)u′(x)dx – формула интегрирования по частям в неопределенном интеграле.

bb

–∫u dv = uv ba − ∫vdu – формула интегрирования по частям в определенном интеграле.

aa

		b				– формула среднего значения; c [a , b].
	●	∫ f (x)dx = f (c)(b −a)
		a
		b
	●	∫ f (x)dx = F(b)− F(a)= F(x)						ba – формула Ньютона-Лейбница.
		a
			b
	●	s = ∫ f (x)dx – площадь криволинейной трапеции
			a
								0 ≤ y ≤ f (x), a ≤ x ≤ b .
			β		– площадь криволинейной трапеции, верхняя граница которой задана параметрически: x = ϕ(t), y = ψ(t), α ≤ t ≤ β .
	●			′
		s = ∫ψ(t)ϕ (t)dt
		α
			1	β
	●	s =		∫ρ2 (ϕ)dϕ – площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах: ρ = ρ(ϕ), α ≤ ϕ ≤ β .
		2		α
			b
	●	L = ∫		′	2				a ≤ x ≤ b .
				1+( f (x)) dx – длина дуги кривой, заданной уравнением y = f (x),
			a
			β
	●	L = ∫		(ϕ′(t))2 +(ψ′(t))2 dt – длина дуги кривой, заданной параметрически:					x = ϕ(t), y = ψ(t), α ≤ t ≤β .
			α
			β
	●	L = ∫		2	′	2
				(ρ(ϕ)) +	(ρ (ϕ))	dϕ – длинадугикривой, заданной в полярных координатах: ρ =ρ(ϕ), α≤ϕ≤β .

α