Типовой вариант контрольной работы

Типовой вариант контрольной работы

Задача 1.

Из 7 экономистов и 4 бухгалтеров случайным образом составляют комиссию в составе 4-х человек. Найдите вероятность того, что в состав комиссии входят:

а) два бухгалтера;

б) менее двух бухгалтеров;

в) хотя бы один бухгалтер.

Решение.

а) ={в комиссии из 4-х человек ровно два бухгалтера}.

.

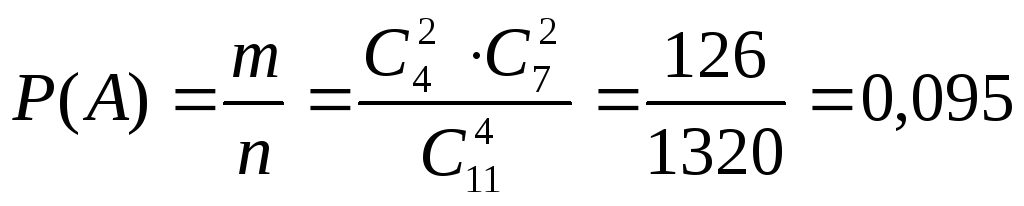б) {в комиссии из 4-х человек менее двух бухгалтеров}. Это значит, в комиссии будет один бухгалтер, либо их вообще не будет. Введем события: ={в комиссии бухгалтеров нет}, ={в комиссии один бухгалтер}. Тогда .

.

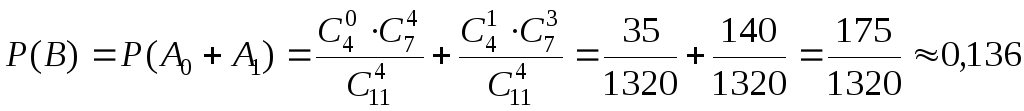в) ={в комиссии хотя бы один бухгалтер}. В комиссии могут присутствовать один, два, три или четыре бухгалтера. Тогда противоположным событием событию является ={в комиссии бухгалтеров нет}.

.

Задача 2. . В классе 40 учеников, из которых 10 отличников. Класс наудачу разделен на 2 равные части. Какова вероятность того, что в каждой части по 5 отличников?

Решение. .

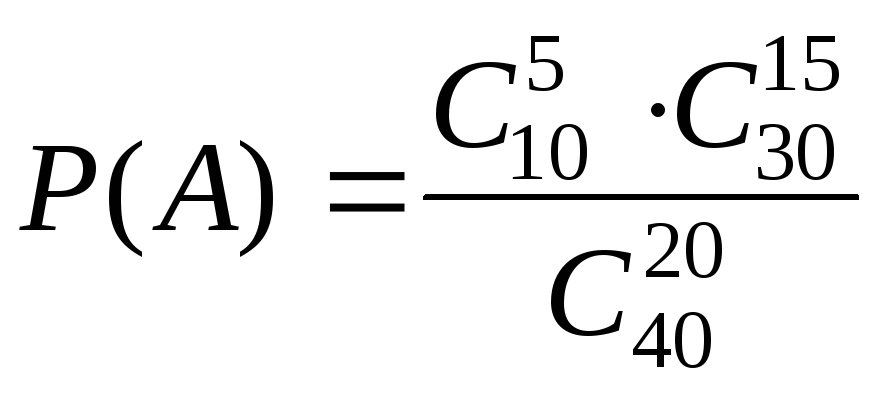Задача 3. Случайным образом 10 книг расставлены на полке. Определить вероятность того, что при этом 3 определенные книги окажутся рядом.

Решение. Чтобы подсчитать число благоприятствующих исходов, надо считать три определенные книги, которые должны быть рядом, одной книгой, и тогда фактически мы переставляем не 10, а 8 книг; но 3 определенные книги также можно переставлять способами, получаем . .

Задача 4. Какова вероятность того, что студенту потребуется не более трех попыток для сдачи экзамена, если вероятность успеха при каждой попытке равна 0,7 независимо от номера попытки?

Решение.

Введем обозначения событий:

- студенту потребуются не более трех попыток для сдачи экзамена;

 - потребуются больше трех попыток;

- i-я попытка безуспешная, i=1,2,3.

.

Задача 5. Партия из 100 деталей подвергается выборочному контролю. Условием непригодности всей партии является наличие хотя бы одной бракованной детали среди пяти проверенных. Какова вероятность для данной партии быть принятой, если она содержит 5% неисправных деталей.

Решение.

={партия деталей будет принята}. Данное событие является произведением пяти событий: , где ={k - я проверенная деталь доброкачественная},.

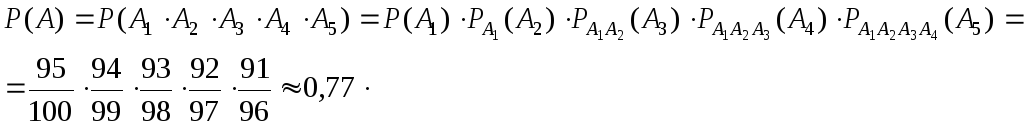
Задача 6. В коробке лежат 4 белых шара и 6 красных. Наудачу, один за другим из коробки извлекается 2 шара. Найти вероятность того, что среди них будет:

а) один красный шар;

б) менее 2-х красных шаров.

Решение. а) Пусть событие А – среди двух извлеченных шаров – ровно один красный. Это событие наступает тогда и только тогда, когда первый из извлеченных шаров – красный, а второй – белый или первый шар – белый, а второй – красный. Тогда описание всех возможностей наступления события равносильно следующему формальному равенству ,

где () – первый (второй) шар – красный, () – первый (второй) шар – белый. События и – несовместны, поэтому, используя теорему сложения вероятностей для несовместных событий, получаем

.

Применяя теперь теорему умножения вероятностей, приходим к равенству

.

Для вычисления вероятностей из правой части последнего равенства используем классическое определение вероятности. Тогда

б) Пусть m – число красных шаров среди двух извлеченных. Тогда искомой является вероятность События и взаимно противоположны, поэтому

Задача 7. В первом наборе 20 деталей и из них 18 - стандартны. Во втором наборе 10 деталей и из них 9 - стандартны. Из второго набора наудачу взята деталь и переложена в первый. Найти вероятность того, что деталь, наудачу извлеченная из первого набора, будет стандартна.

Решение. Введем обозначения для событий: – из первого набора извлечена стандартная деталь, – из второго набора извлечена стандартная деталь, – из второго набора извлечена нестандартная деталь.

.

- событие, состоящее в том, что выбранная деталь оказалась стандартной при выполнении гипотезы (i=1 ,2). Из условия задачи следует:

.

По формуле полной вероятности имеем: .

Задача 8. В первом ящике 2 красных и 5 синих папок, во втором – 4 красных и 3 синих. Из первого ящика переложили 2 папки во второй, после чего из второго ящика наугад достали одну папку. Какова вероятность, что она красного цвета?

Решение.

1. Определим событие А - выбранная папка оказалась красного цвета.

2. Пусть событие H₁ состоит в том, что две выбранные папки красного цвета, H₂ – одна красного цвета, а другая – синего, H₃ - две выбранные папки синего цвета.

3. .

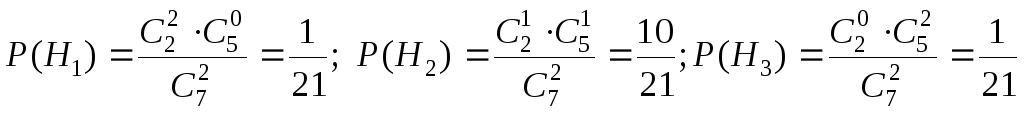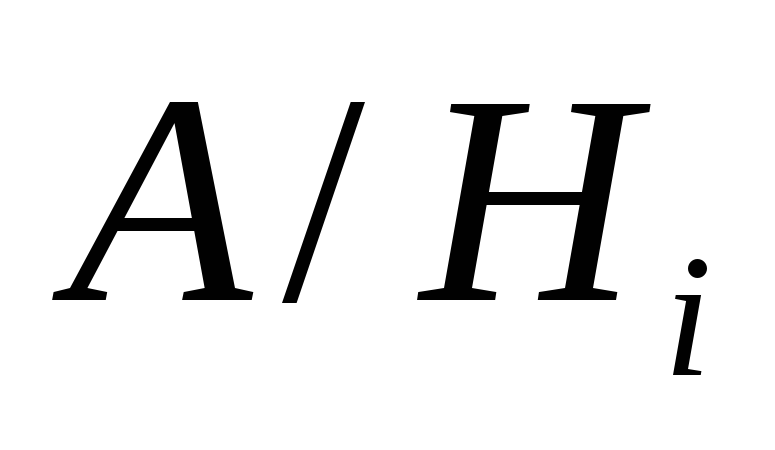4. - событие, состоящее в том, что выбранная папка оказалась красного цвета при выполнении гипотезы (i=1 ,2, 3). Из условия задачи следует:

5. Найдем искомую вероятность по формуле полной вероятности:

.

Задача 9. 60% учащихся в школе- девочки, 80% девочек и 75% мальчиков имеют билеты в театр. В учительскую принесли кем-то потерянный билет. Какова вероятность того, что этот билет принадлежал девочке.

Решение. Пусть - событие, что у ученика есть билет. Определим гипотезы:

-ученик – девочка; -ученик- мальчик.

По формуле Бейеса:

.

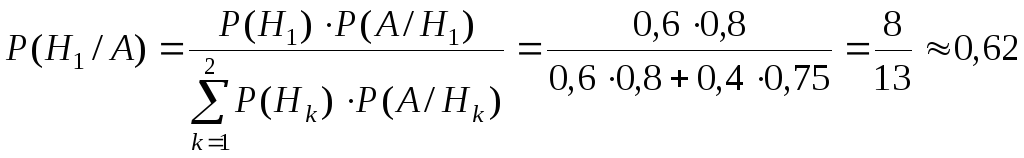Задача 10. Вероятность выигрыша по одному билету денежно-вещевой лотереи равна 0,2. Какова вероятность того, что из шести приобретённых билетов два билета окажутся выигрышными?

Решение. Эксперимент состоит в том, что последовательно проверяются шесть билетов, т.е. проводится шесть повторных независимых испытаний. Каждое испытание имеет два исхода: билет выигрышный и билет невыигрышный. Вероятность выигрыша в каждом испытании постоянна. Следовательно, схема Бернулли выполняется.

.

Задача 11. Найдите вероятность осуществления от двух до четырёх разговоров по телефону при наблюдении пяти независимых вызовов, если вероятность того, что разговор состоится, равна 0,7.

Решение. .

Задача 12. Бракованные изделия, выпускаемые некоторым заводом, составляют в среднем 1,5%. Какое наивероятнейшее количество бракованных изделий будет в партии из 220 штук? Сколько нужно закупить изделий, чтобы наивероятнейшее число годных было равно 250?

Решение. Наивероятнейшее число успехов m₀ в серии из испытаний при условии, что вероятность наступления интересующего нас события в каждом испытании постоянна и равна p, удовлетворяет следующему неравенству:

.

Имеем (общее число изделий); (вероятность брака); (вероятность годного изделия).

Получим: .

.

Так как наивероятнейшее число бракованных изделий не может быть дробным числом, то единственным ответом будет .

Определим, сколько нужно закупить изделий , чтобы наивероятнейшее число годных было равно . Здесь вероятность интересующего нас события (годного изделия) , тогда :

,

или ; .

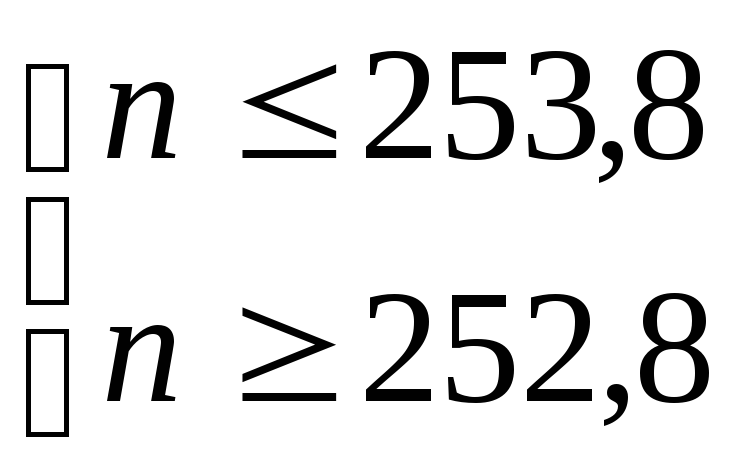Данной системе удовлетворяет единственное целое число n = 253.

Задача 13. Вероятность изготовления бракованной отливки равна 0,002. Определить вероятность того, что из выпущенных 500 отливок количество бракованных составит: а) 2; б) более двух.

Решение. В этой задаче значение велико, вероятность мала, произведение .

а) . Найти вероятность можно по формуле Бернулли, но это нецелесообразно ввиду громоздкости вычислений. Воспользуемся формулой Пуассона .

Вероятность можно найти, воспользовавшись таблицей значений функции Пуассона (приложение 6): P₅₀₀(2)=0,1839.

б) , т.е. m = 3, 4, …, 500. Необходимо найти .

Удобнее перейти к противоположному событию , тогда .

Для вычисления каждого слагаемого используем формулу Пуассона при и .

Получаем, пользуясь таблицей приложения 6:

.

Задача 14. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 попал в цель хотя бы один раз?

Решение. Пусть – событие, что при – выстрелах стрелок попадает в цель хотя бы один раз.

. По условию задачи имеем:

. Значит .

Задача 15. Найти вероятность того, что событие появится ровно 80 раз в 400 испытаниях, если вероятность события в каждом испытании равна 0,2.

Решение. Так как и принимают большие значения, то применяем локальную теорему Лапласа:

.

.

Задача 16. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян число проросших будет заключено между 790 и 830.

Решение. Применяем интегральную теорему Лапласа:

.

где .

По таблице (приложение 2) определяем значения функции Лапласа:

, . Таким образом:

.

Задача 17. В страховой компании 10 000 клиентов. Страховой взнос – 2 000 у.е. Вероятность страхового случая . Страховая выплата – 200 000 у.е. Определить размер прибыли страховой компании с вероятностью .

Решение. Прибыль млн. у.е. где - число страховых случаев. Найдем такое , чтобы . Применяем интегральную теорему Лапласа:

.

. Отсюда получим:

. или . Из приложения 2 имеем:

. Отсюда . Окончательно:

млн. у.е.

Следствия из интегральной теоремы Муавра-Лапласа

Пусть выполнены условия применимости интегральной теоремы Муавра-Лапласа.

Следствие 1. Вероятность того, что число наступлений события А в n повторных независимых испытаниях будет отличаться от величины не более чем на (по абсолютной величине), вычисляется по формуле:

Доказательство данной следует из интегральной теоремы Муавра-Лапласа.

Следствие 2. Вероятность того, что доля наступлений события А в n повторных независимых испытаниях будет отличаться от вероятности p наступления этого события в одном испытании не более чем на (по абсолютной величине), вычисляется по формуле:

Пример. Подлежат исследованию 1 000 проб руды. Вероятность промышленного содержания металла в каждой пробе равна 0,15. Найти границы, в которых с вероятностью 0,9973 будет заключено число проб руды с промышленным содержанием металла.

Решение. и . По условию задачи имеем:

По таблице значений нормированной функции Лапласа (приложение 2) найдем такое , что ,

Тогда и .

Искомые границы: . Таким образом, с вероятностью 0,9973 число проб руды с промышленным содержанием металла (из данных 1000 проб) попадет в интервал (116; 184).

Пример. В лесхозе приживается в среднем 80 саженцев. Сколько саженцев надо посадить, чтобы с вероятностью 0,9981 можно было утверждать, что доля прижившихся саженцев будет находиться в границах от 0,75 до 0,85.

Решение. – вероятность прижиться для каждого из саженцев, . Пусть – необходимое число саженцев (искомая величина данной задачи) и – число прижившихся из них, тогда – доля прижившихся саженцев. По условию,

Данные границы для доли симметричны относительно величины, поэтому неравенство равносильно неравенству

Следовательно, вероятность 0,9981 – это та самая вероятность, которая вычисляется по следствию 2 из интегральной теоремы Муавра-Лапласа при , :

По таблице нормированной функции Лапласа (приложение 2) найдем такое значение , что Это значение: Тогда

и

Заметим, что значение округлено до целых в большую сторону, чтобы обеспечить, как говорят, “запас по вероятности”.

Задача 18. При обработке линз в среднем 3 из 100 имеют брак. Сколько линз следует обработать, чтобы с вероятностью 0,95 можно было ожидать, что отклонение доли брака от его вероятности не превысит 0,01 (по абсолютной величине)?

Решение. Здесь – вероятность того, что линза бракованная, тогда . Требуется найти число n при заданной надежности . Воспользуемся следствием из интегральной теоремы Муавра-Лапласа, которое выражается формулой

,

где – частота (доля) появления события А в независимых испытаниях. По условию задачи , . По таблице значений функции Лапласа, зная , находим . Тогда , отсюда , .

Следовательно, нужно обработать линз, чтобы с вероятностью 0,95 можно было утверждать, что отклонение доли появления бракованной линзы от вероятности линзе быть бракованной (равной 0,03) не превосходит 0,01 (по абсолютной величине).

10