МАТЕМАТИКА (ІДЗ) / Rozdil2_15
.doc-
ЛІНІЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
ІЗ СТАЛИМИ КОЕФІЦІЄНТАМИ
Диференціальне
рівняння
- го порядку називається лінійним, якщо
воно лінійне відносно шуканої функції
та
її похідних
тобто
воно має такий вигляд
(2.54)
Якщо
- постійні, а
- деяка неперервна на
проміжку
функція, то рівняння (2.54) називається
лінійним диференціальним рівнянням із
сталими коефіцієнтами.
Якщо
то рівняння (2.54) називається лінійним
неоднорідним диференціальним рівнянням
(ЛНДР) із сталими коефіцієнтами. Якщо ж
то рівняння (2.54) має вигляд
(2.55)
і називається лінійним однорідним диференціальним рівнянням (ЛОДР) із сталими коефіцієнтами.
Загальний
розв’язок
ЛНДР (2.54) визначається як сума загального
розв’язку
ЛОДР
(2.55) і якого-небудь частинного розв’язку
ЛНДР (2.54), тобто
(2.56)
Розглянемо ЛНДР із сталими коефіцієнтами другого порядку
(2.57)
і відповідне йому ЛОДР
(2.58)
Загальний розв’язок (2.57) визначається за формулою (2.56).
Для
знаходження загального розв’язку
ЛОДР (2.58)
складаємо характеристичне рівняння
(2.59)
Можливі такі випадки:
-
Корені характеристичного рівняння (2.59) дійсні та різні
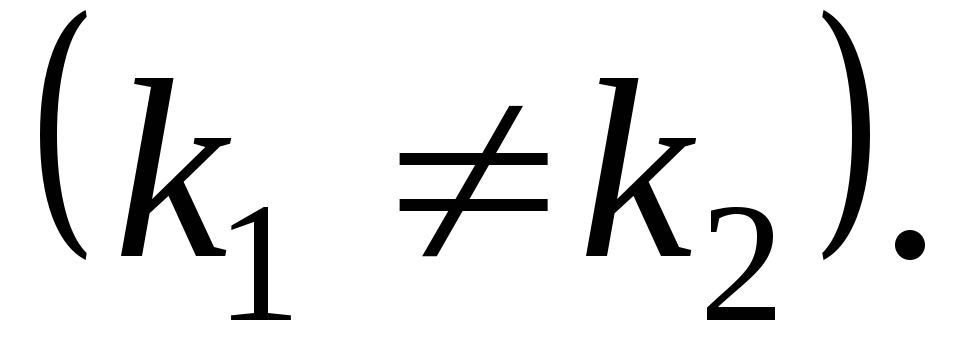
Тоді
два лінійно незалежні розв’язки
ЛОДР (2.58)
мають
такий
вигляд
і загальний розв’язок
(2.60)
2. Корені характеристичного рівняння (2.59) комплексні
Тоді
і
(2.61)
-
Корені характеристичного рівняння (2.59) рівні
Тоді
і
(2.62)
Якщо
- загальний розв’язок
ЛОДР (2.58)
де
- два лінійно незалежних розв’язки
ЛОДР (2.58),
то
частинний
розв’язок
ЛНДР (2.57)
шукається методом варіації
довільних сталих
(2.63)
знаходяться із
системи рівнянь
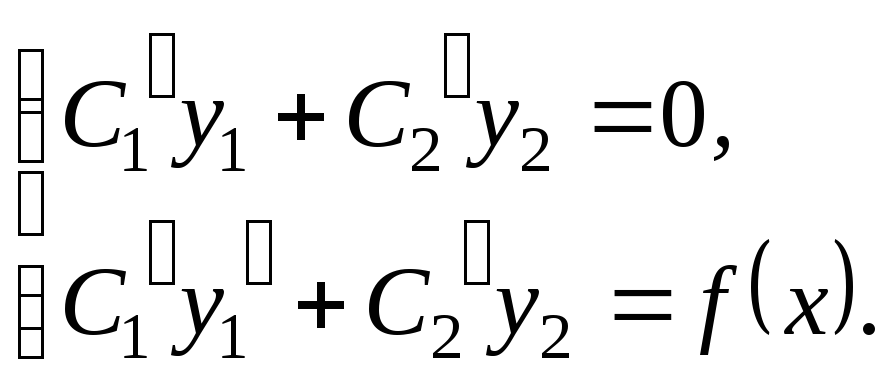(2.64)
Нехай
тоді
У випадку, коли
права частина ЛНДР
спеціального
вигляду, частинний розв’язок ЛНДР можна шукати, не застосовуючи методу варіації довільних сталих.
-
Нехай права частина ЛНДР (2.57) має такий вигляд
(2.65)
де
- многочлен
-
го степеня. Тоді частинний розв’язок
ЛНДР
шукаємо у вигляді
(2.66)
де
- многочлен
-
го степеня з невизначеними коефіцієнтами,
а
- кратність числа
,
як кореня характеристичного рівняння
(2.59)
(якщо
не є коренем характеристичного рівняння
(2.59), то
).
-
Нехай права частина ЛНДР (2.57) має такий вигляд
(2.67)
Тоді
(2.68)
де
- многочлени степеня
з невизначеними коефіцієнтами, а
- кратність числа
,
як кореня
характеристичного рівняння (2.59).
Підставляючи (2.66) або (2.68) в рівняння
(2.57), визначаємо коефіцієнти у многогчлена
або у многочленів
АР-2.15
1. Знайти загальні розв’язки диференціальних рівнянь:
а)
б)
в)
г)
2. Знайти частині розв’язки диференціальних рівнянь, що задовільняють початкові умови.
а)
б)
3. Знайти загальний розв’язок диференціального рівняння методом варіації довільних сталих
СР-2.15
Знайти загальні розв’язки диференціальних рівнянь:
1.
2.
-
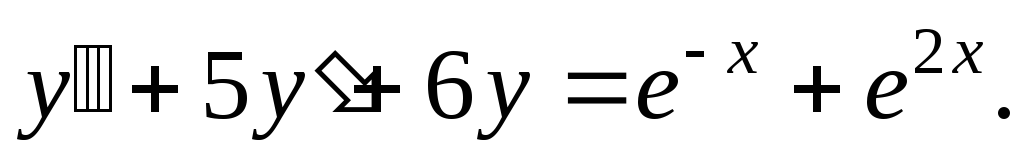4.
ІДЗ-2.15
1. Знайти загальні розв’язки диференціальних рівнянь.
1.1. а)
б)
в)
1.2. а)
б)
в)
1.3. а)
б)
в)
1.4. а)
б)
в)
1.5. а)
б)
в)
1.6. а)
б)
в)
1.7. а)
б)
в)
1.8. а)
б)
в)
1.9. а)
б)
в)
1.10. а)
б)
в)
1.11. а)
б)
в)
1.12. а)
б)
в)
1.13. а)
б)
в)
1.14. а)
б)
в)
1.15. а)
б)
в)
1.16. а)
б)
в)
1.17.
а)
б)
в)
1.18. а)
б)
в)
1.19.
а)
б)
в)
1.20. а)
б)
в)
1.21. а)
б)
в)
1.22. а)
б)
в)
1.23. а)
б)
в)
1.24. а)
б)
в)
1.25. а)
б)
в)
1.26. а)
б)
в)
1.27. а)
б)
в)
1.28. а)
б)
в)
1.29. а)
б)
в)
1.30. а)
б)
в)
2. Знайти частинний розв’язок диференціального рівняння, що задовільняє початкові умови :
(варіанти
1-10);
(варіанти
11-20);
(варіанти
21-30).
2.1. а)
б)
2.2. а)
б)
2.3. а)
б)
2.4. а)
б)
2.5. а)
б)
2.6. а)
б)
2.7. а)
б)
2.8. а)
б)
2.9. а)
б)
2.10.а)
б)
2.11.а)
б)
2.12.а)
б)
2.13.а)
б)
2.14.а)
б)
2.15.а)
б)
2.16.а)
б)
2.17.а)
б)
2.18.а)
б)
2.19.а)
б)
2.20.а)
б)
2.21.а)
б)
2.22.а)
б)
2.23.а)
б)
2.24.а)
б)
2.25.а)
б)
2.26.а)
б)
2.27.а)
б)
2.28.а)
б)
2.29.а)
б)
2.30.а)
б)
3. Знайти загальний розв’язок диференціального рівняння методом варіації довільних сталих.
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
3.9.
3.10.
3.11.
3.12.
3.13.
3.14.
3.15.
3.16.
3.17.
3.18.
3.19.
3.20.
3.21.
3.22.
3.23.
3.24.
3.25.
3.26.
3.27.
3.28.
3.29.
3.30.
РОЗВ’ЯЗОК ТИПОВОГО ВАРІАНТА
1. Знайти загальні розв’язки диференціальних рівнянь:
а)
б)
в)
а)
Записуємо характеристичне рівняння
Це
рівняння має корені
- дійсні різні. Тоді загальний
розв’язок має вигляд
б)
Характеристичне рівняння
має корені
- дійсні рівні. Тоді загальний розв’язок
має
вигляд
в)
Характеристичне
рівняння
має корені
-
комплексні спряжені. В даному випадку загальний розв’язок має вигляд
2. Знайти частинні розв’язки диференціальних рівнянь, що задовільняють початкові умови:
а)
б)
а)
Характеристичне рівняння
має
корені
Тоді загальний розв’язок
відповідного однорідного рівняння має
вигляд
Частинний розв’язок неоднорідного рівняння шукатимемо у вигляді
(
)
Знайдемо
Підставимо
вирази для
в
початкове рівняння та скоротимо на
Прирівнявши
коефіцієнти при однакових степенях
одержимо
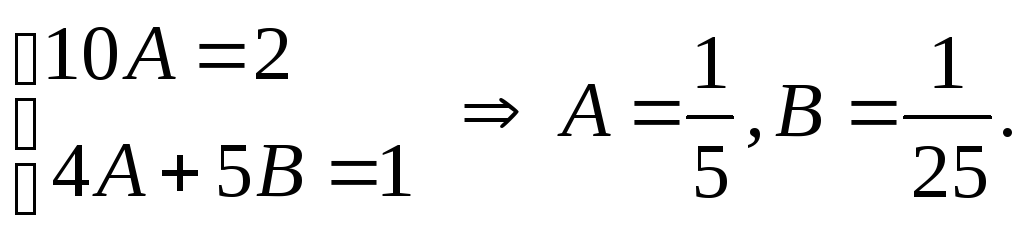
Тоді
і загальний розв’язок
ЛНДР має такий вигляд
Знайдемо
частинний розв’язок
ЛНДР, що задовільняє початковим умовам
Одержимо
для визначення
систему рівнянь
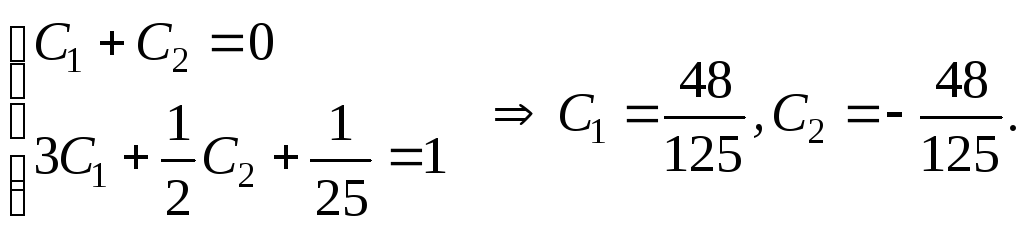
Тоді розв’язок задачі має вигляд
б)
Характеристичне рівняння ЛОДР
має
корені
Загальний розв’язок
ЛОДР
Частинний
розв’язок
ЛНДР шукаємо у вигляді (
)
