
Mathcad - ЛР5
.pdfМинистерство образования Российской Федерации Санкт - Петербургский государственный политехнический университет
Институт менеджмента и информационных технологий
Кафедра ПО ВТ и АС
Лабораторный практикум по курсу вычислительной математики
ОТЧЕТ
по лабораторной работе №5
Тема:
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ и ДИФФЕРЕНЦИРОВАНИЕ
Выполнил: ______________
Группа: _____
Вариант: 14
Проверил: Царев В.А.
Отметка о зачете __________________
" ___ " ______________ 2006 г.
Череповец
2006

Задача 5.1. Функция y = f (x) задана на отрезке [a,b] . Вычислить значение интеграла
òb |
f (x)dx для различных значений количества отрезков разбиения n = 1,2,...,10 (или |
a |
|
соответственно с различным значением шага h = b -n a) , используя следующие формулы:
А) левых прямоугольников; В) центральных прямоугольников; С) правых прямоугольников;
D) трапеций.
Для каждого случая A)-D) построить график зависимости абсолютной погрешности
результата от n = 1,2,...,10 (или h ) и |
график теоретической оценки абсолютной |
погрешности в зависимости от n =1,2,...,10 |
(или h ). Сделать выводы. |
Теоретический материал:
Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Существует множество способов вычисления интеграла. Формулы четырех способов решения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
Формула левых прямоугольников: S= hå f (xi ) ; |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
M1 (b - a)2 |
i=0 |
|
|
|
|
|||||||||
оценка погрешности |
|
R = |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
Формула правых прямоугольников: S= hå f (xi ) ; |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
M1 (b - a)2 |
|
|
|
|
i=1 |
|
|
|
|
||||||
оценка погрешности |
R = |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
xi + xi+1 |
|
|
Формула центральных прямоугольников: S= hå f ( |
) ; |
|
||||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
M 2 (b - a)3 |
|
|
|
|
|
i=0 |
2 |
|
|
|||||||||
оценка погрешности |
R = |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
24n2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
æ |
|
|
f (x |
0 |
) + f (x |
n |
) |
n−1 |
ö |
|
|
||||||||||
Формула трапеций: |
S= hç |
|
|
|
|
|
|
|
|
+ å f (xi |
)÷ ; |
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
ø |
|
|
||||
оценка погрешности |
R = |
|
M 2 (b - a)3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
12n2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Исходные данные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
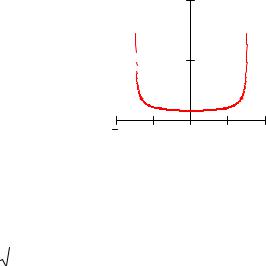
Задана функция f(x) := |
|
|
|
|
1 |
|
|
|
|
на отрезке [2;2] |
|
a := −2 |
b := 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
9 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4
f(x) |
|
|
2 |
|
|
||||
|
|
|||
|
|
|
|
|
4 |
|
2 |
0 |
2 |
4 |
|
x
Решение задачи:
Найдём определенный интеграл аналитически:
2 |
|
1 |
|
|
|
|
|
|
|
|
x |
|
2 |
|
2 |
|
- 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ò−2 |
|
|
|
|
× dx = arcsin |
|
|
|
|
= arcsin |
|
- arcsin |
3 |
|||||
|
|
|
|
3 |
|
|
3 |
|||||||||||
9 - x2 |
|
|
−2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
true := asin |
æ 2 |
ö |
- asin |
æ -2 ö |
= (1.45945531245393) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
è 3 |
ø |
è 3 ø |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
A) Произведем вычисление определенного интеграла методом левых прямоугольников:
IntLeftRect(f , a, b , n) := |
h ¬ |
b - a |
|||||||
n |
|
||||||||
|
|
|
|
|
|
||||
|
|
|
|
for |
i Î 0 .. n |
||||
|
|
|
|
xi ¬ a + h×i |
|||||
|
|
|
|
S ¬ 0 |
|||||
|
|
|
|
for |
i Î 0 .. n - 1 |
||||
|
|
|
|
S ¬ S + f(xi) |
|||||
|
|
|
|
S ¬ h×S |
|||||
|
|
|
|
S |
|
|
|
||
|
|
|
|
|
|
|
|
||
E_Leftn := |
true - integraln |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
||
|
0 |
|
0.329399069545899 |
|
|||||
|
1 |
|
0.10163854521265 |
|
|||||
|
2 |
|
0.048514093223115 |
|
|||||
|
3 |
|
0.028198397565906 |
|
|||||
E_Left = |
4 |
|
0.01836817310573 |
|
|||||
|
5 |
|
0.012890550963647 |
|
|||||
|
6 |
|
9.53469699306364·10 -3 |
|
|||||
|
7 |
|
7.33342390714387·10 -3 |
|
|||||
|
8 |
|
5.81305177929425·10 -3 |
|
|||||
|
9 |
|
4.71971170130225·10 -3 |
|
|||||
n := 0 .. 9
integraln := IntLeftRect(f , a, b, n + 1)
|
|
0 |
|
0 |
1.78885438199983 |
|
1 |
1.56109385766658 |
|
2 |
1.50796940567705 |
|
3 |
1.48765371001984 |
integral = |
4 |
1.47782348555966 |
|
5 |
1.47234586341758 |
|
6 |
1.468990009447 |
|
7 |
1.46678873636108 |
|
8 |
1.46526836423323 |
|
9 |
1.46417502415523 |
|
|
|

df(x) := d f(x) |
|
|
|
|
|
|
|
|
|
|
|
absdf(x) := |
df(x) |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
M1 := absdf(2) |
n := 0 .. 9 |
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
M1 = 0.178885 |
|
|
|
absdf(z) 0.1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
2 |
0 |
2 |
||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
z |
|
|
|
R_Left(f , a, b , n) := (b - a)2 ×M1
2×n
2
R_Left(f , a, b, n)
1
E_Leftn
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||
На вышепредставленном рисунке видно, что теоретически вычисленная погрешность значительно превышает практическую.
B) Произведем вычисление определенного интеграла методом центральных прямоугольников:
IntСentr(f , a , b, n) := |
h ¬ |
b - a |
|
|
|
|
n := 0 .. 9 |
|
|
||||
n |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
for |
i Î 0 .. n |
|
|
|
integraln := IntСentr(f , a, b, n + 1) |
||||||
|
|
xi ¬ a + h×i |
|
|
|
|
|
|
|||||
|
|
S ¬ 0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|||||
|
|
for |
i Î 1 .. n |
|
|
|
|
0 |
1.33333333333333 |
||||
|
|
|
|
|
|
æx |
|
h |
ö |
1 |
1.41421356237309 |
||
|
|
S ¬ S + f |
+ |
2 |
1.43672232115811 |
||||||||
|
|||||||||||||
|
|
|
|
|
|
è |
i−1 |
2 ø |
|||||
|
|
S ¬ h×S |
|
3 |
1.44592376270231 |
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
integral = |
4 |
1.45052656275081 |
|||||
|
|
S |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
5 |
1.45314060011584 |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
6 |
1.45476123518253 |
|
E_Centrn := |
true - integraln |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
7 |
1.45583272997773 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1.45657688052445 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1.45711415927405 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0.126121979120599 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
0.045241750080838 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
0.022732991295821 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 |
|
|
0.013531549751618 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E_Centr = |
|
4 |
|
|
8.92874970312585·10 -3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
5 |
|
|
6.31471233809422·10 -3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
6 |
|
|
4.69407727139837·10 -3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
7 |
|
|
3.62258247620195·10 -3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
8 |
|
|
2.87843192948523·10 -3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
9 |
|
|
2.34115317988359·10 -3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
df2(x) := |
|
f(x) absdf2(x) := |
df2(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
dx |
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
M2 := absdf2(2) |
n := 0 .. 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
M2 = 0.304105 |
|
|
|
|
|
|
|
|
|
|
|
|
absdf2(z) 0.2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|||
|
|
|
|
|
|
|
|
(b - a) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R_Centr(f , a, b, n) := |
|
|
|
×M2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24×n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R_Centr(f , a, b, n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E_Centrn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
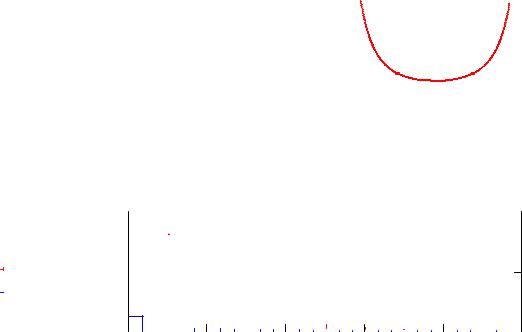
На вышепредставленном рисунке видно, что теоретически вычисленная погрешность значительно превышает практическую.

C) Произведем вычисление определенного интеграла методом правых прямоугольников:
IntRightRect(f , a, b, n) := |
h ¬ |
b - a |
|||||||
n |
|
||||||||
|
|
|
|
|
|
||||
|
|
|
|
for |
i Î 0 .. n |
||||
|
|
|
|
xi ¬ a + h×i |
|||||
|
|
|
|
S ¬ 0 |
|||||
|
|
|
|
for |
i Î 1 .. n |
||||
|
|
|
|
S ¬ S + f(xi) |
|||||
|
|
|
|
S ¬ h×S |
|||||
|
|
|
|
S |
|
|
|
||
|
|
|
|
|
|
|
|
||
E_Rightn := |
true - integraln |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
||
|
0 |
|
0.329399069545899 |
|
|||||
|
1 |
|
0.10163854521265 |
|
|||||
|
2 |
|
0.048514093223115 |
|
|||||
|
3 |
|
0.028198397565906 |
|
|||||
E_Right = |
4 |
|
0.01836817310573 |
|
|||||
|
5 |
|
0.012890550963647 |
|
|||||
|
6 |
|
9.53469699306364·10 -3 |
|
|||||
|
7 |
|
7.33342390714364·10 -3 |
|
|||||
|
8 |
|
5.81305177929425·10 -3 |
|
|||||
|
9 |
|
4.71971170130203·10 -3 |
|
|||||
n := 0 .. 9
integraln := IntRightRect(f , a, b, n + 1)
|
|
0 |
|
0 |
1.78885438199983 |
|
1 |
1.56109385766658 |
|
2 |
1.50796940567705 |
|
3 |
1.48765371001984 |
integral = |
4 |
1.47782348555966 |
|
5 |
1.47234586341758 |
|
6 |
1.468990009447 |
|
7 |
1.46678873636108 |
|
8 |
1.46526836423323 |
|
9 |
1.46417502415523 |
|
|
|
df(x) := d f(x) |
|
|
|
|
|
|
|
|
|
|
|
absdf(x) := |
df(x) |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
M1 := absdf(2) |
n := 0 .. 9 |
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
M1 = 0.178885 |
|
|
|
absdf(z) 0.1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
2 |
0 |
2 |
||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
R_Right(f , a, b , n) := (b - a)2 ×M1
2×n
2 |
|
|
|
|
|
R_Right(f , a, b, n) |
|
|
|
|
|
1 |
|
|
|
|
|
E_Rightn |
|
|
|
|
|
0 0 |
2 |
4 |
6 |
8 |
10 |
|
|
|
n |
|
|
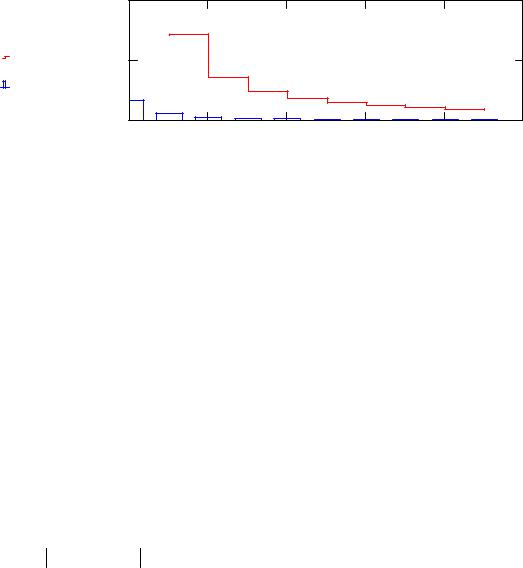
На вышепредставленном рисунке видно, что теоретически вычисленная погрешность значительно превышает практическую.
D) Произведем вычисление определенного интеграла методом трапеций:
Trapeсia(f , a, b, n) := |
h ¬ |
b - a |
|||
|
n |
|
|||
|
|
|
|||
|
for |
i Î 0 .. n |
|||
|
xi ¬ a + h×i |
||||
|
S ¬ |
|
f(x0) + f(xn) |
||
|
|
|
|
||
2 |
|||||
|
|
||||
|
for |
i Î 1 .. n - 1 |
|||
|
S ¬ S + f(xi) |
||||
|
S ¬ h×S |
||||
|
S |
|
|
|
|
E_Trapecian := true - integraln
|
|
0 |
|
0 |
3.90710783354556 |
|
1 |
0.10163854521265 |
|
2 |
0.048514093223115 |
|
3 |
0.028198397565906 |
E_Trapecia = |
4 |
0.01836817310573 |
|
5 |
0.012890550963647 |
|
6 |
9.53469699306364·10 -3 |
|
7 |
7.33342390714387·10 -3 |
|
8 |
5.81305177929425·10 -3 |
|
9 |
4.71971170130225·10 -3 |
n := 0 .. 9
integraln := Trapeсia(f , a, b, n + 1)
|
|
0 |
|
0 |
5.3665631459995 |
|
1 |
1.56109385766658 |
|
2 |
1.50796940567705 |
|
3 |
1.48765371001984 |
integral = |
4 |
1.47782348555966 |
|
5 |
1.47234586341758 |
|
6 |
1.468990009447 |
|
7 |
1.46678873636108 |
|
8 |
1.46526836423323 |
|
9 |
1.46417502415523 |
|
|
|

df2(x) := |
d2 |
|
f(x) |
absdf2(x) := |
|
df2(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 := absdf2(2) |
n := 0 .. 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
M2 = 0.304105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
absdf2(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(b - a) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
R_Trapecia(f , a, b, n) := |
×M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
12×n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
R_Trapecia(f , a, b, n) |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E_Trapecian |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
|
4 |
|
6 |
|
|
|
|
|
8 |
|
|
|
|
10 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
На вышепредставленном рисунке видно, что теоретически вычисленная погрешность значительно превышает практическую для подавляющего большинства n.
Сравнение использованных методов по точности:
n := 9
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
(Vi)2 |
|
|
|
|
|
|||
norma_1(V , n) := å |
|
Vi |
|
norma_2(V , n) := å |
norma_c(V , n) := |
|
for i Î 0 .. n |
|||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
i = 0 |
|
|
i = 0 |
|
|
|
|
si ¬ |
Vi |
|
||
|
|
|
|
|
|
|
|
|
|
max(s) |
||
Функция нахождения максимальной из норм:
max_P(V , n) := s1 ¬ norma_1(V , n) s2 ¬ norma_2(V , n) s3 ¬ norma_c(V , n)
max(s)

Произведем сравнение точности использованных методов на основе сравнения норм векторов погрешностей, полученных практически:
max_P(E_Left , n) = 0.56640971399775 |
min(E_Left) = 4.71971170130225 ´ 10- 3 |
max_P(E_Centr , n) = 0.236407977147066 |
min(E_Centr) = 2.34115317988359 ´ 10- 3 |
max_P(E_Right, n) = 0.56640971399775 |
min(E_Right) = 4.71971170130203 ´ 10- 3 |
max_P(E_Trapecia , n) = 4.14411847799742 |
min(E_Trapecia) = 4.71971170130225 ´ 10- 3 |
Вывод: В ходе проведенного вычиcлительного эксперимента метод центральных
прямоугольников показал высокую стабильность при различных n и наивысшую точность среди всех использованных методов.
Задача 5.2. Для функции из задачи 5.1 вычислить значение интеграла òb f (x)dx методом
a
Симпсона для различных значений количества отрезков разбиения n = 2,4,...,20 (или соответственно с различным значением шага h = b -n a) . Построить график зависимости
абсолютной погрешности результата от n = 2,4,...,10 (или h ) и график теоретической оценки абсолютной погрешности в зависимости от n = 2,4,...,10 (или h ). Сделать выводы, сравнивая с результатами, полученными в задаче 5.1.
Решение задачи:
Simpson(f , a , b, n) := |
h ¬ |
b - a |
||||||||
|
|
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
for |
i Î 0 |
.. n |
|||||||
|
xi ¬ a + h×i |
|||||||||
|
S ¬ f(x0) + f(xn) |
|||||||||
|
for |
i Î 1 |
.. æ |
n |
ö |
|
||||
|
||||||||||
|
|
|
|
|
è 2 ø |
|
||||
|
S ¬ S + 4×f(x2× |
|||||||||
|
for |
i Î 1 |
.. |
n - 1 |
|
|||||
|
||||||||||
|
|
|
|
|
2 |
|
||||
|
S ¬ S + 2×f(x2× |
|||||||||
|
S ¬ |
h |
×S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
i-1)
i)
integral := 0 |
|
|
|
||
n := 2 , 4 .. 20 |
|
n1 := 0 .. 9 |
|||
integralæ n |
|
ö := Simpson(f , a, b , n) |
|||
ç |
|
-1÷ |
|
||
|
|
||||
è 2 |
|
ø |
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
2.08145847688878 |
|
|
|
1 |
|
1.46317366080426 |
|
|
|
2 |
|
1.46047134933109 |
|
|
|
3 |
|
1.45983374514149 |
|
integral = |
4 |
|
1.45962553702043 |
|
|
|
|
5 |
|
1.45954235454975 |
|
|
|
6 |
|
1.45950415993736 |
|
|
|
7 |
|
1.45948473210551 |
|
|
|
8 |
|
1.45947404176071 |
|
|
|
9 |
|
1.45946778090111 |
|
|
|
|
|
|
|
E_Simpsonn1 := true - integraln1
|
d4 |
|
|
|
|
df4(x) := |
f(x) absdf4(x) := |
df4(x) |
|
||
4 |
|
||||
|
|
|
|
||
|
dx |
3 |
|||
|
|
|
|||
M4 := absdf4(2) |
n := 0 .. 9 |
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
M4 = 2.651082 |
|
|
|
absdf4(z) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(b - a)5 |
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
0 |
|
2 |
|||||||||
|
|
|
|
||||||||||||
R_Simpson(f , a, b, n) := |
|
×M4 |
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
|
z |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
180×n |
|
|
|
|
|
|
|
|
|
|
|
|
|
20
R_Simpson(f , a, b, n)
E_Simpsonn 10
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
||||||
|
|
|
|
|
|
n |
|
|
|
|
|
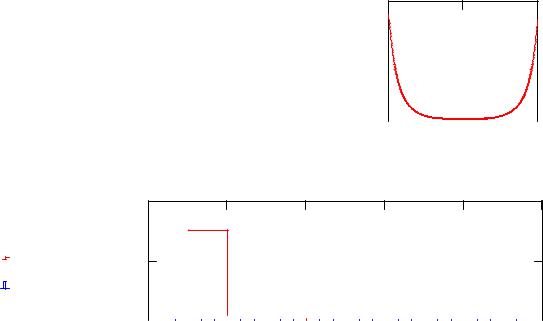
На вышепредставленном рисунке видно, что теоретически вычисленная погрешность значительно превышает практическую.
Произведем сравнение точности использованных методов на основе сравнения норм векторов погрешностей:
max_P(E_Left , 9) = 0.56640971399775 |
min(E_Left) = 4.71971170130225 ´ 10− 3 |
|||
max_P(E_Centr , 9) = 0.236407977147066 |
min(E_Centr) = 2.34115317988359 ´ 10− 3 |
|||
max_P(E_Right, 9) = 0.56640971399775 |
min(E_Right) = 4.71971170130203 ´ 10− 3 |
|||
max_P(E_Trapecia , 9) = 4.14411847799742 |
min(E_Trapecia) = 4.71971170130225 ´ 10− 3 |
|||
max_P(E_Simpson , 9) = 0.627482713901151 |
min(E_Simpson) = 1.24684471785041 ´ 10− 5 |
|||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0.622003164434844 |
|
|
|
1 |
3.7183483503247·10 -3 |
|
|
|
2 |
1.0160368771579·10 -3 |
|
|
|
3 |
3.7843268755644·10 -4 |
|
|
E_Simpson = |
4 |
1.7022456649296·10 -4 |
|
|
|
5 |
8.70420958194451·10 -5 |
|
|
|
6 |
4.88474834225983·10 -5 |
|
|
|
7 |
2.94196515797651·10 -5 |
|
|
|
8 |
1.87293067746008·10 -5 |
|
|
|
9 |
1.24684471785041·10 -5 |
|
|
