Mathcad - ЛР3

Министерство образования Российской Федерации Санкт - Петербургский государственный политехнический университет

Институт менеджмента и информационных технологий

Кафедра ПО ВТ и АС

Лабораторный практикум по курсу вычислительной математики

ОТЧЕТ

по лабораторной работе №3

Тема:

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ

Выполнил: _______________

Группа: _____

Вариант: 14

Проверил: Царев В.А.

Отметка о зачете __________________

" ___ " ______________ 2006 г.

Череповец

2006

Задача 3.1. Даны два уравнения f(x)=0 и g(x)=0. Найти с точностью ε = 10−10 все корни уравнений, содержащиеся на отрезке [a, b]. Для решения задачи использовать метод бисекции. Найти корни с помощью встроенной функции root пакета MATHCAD.

	ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1.	Найти аналитическое решение уравнения f(x)=0.
2.	Используя пакет MATHCAD, локализовать корни f(x)=0 графически.
3.	Используя программу bisec (см. ПРИЛОЖЕНИЕ 2.B), найти корни уравнения f(x)=0 с точностью ε
помощью метода бисекции.
4.	Используя встроенную функцию root пакета MATHCAD, найти корни уравнения f(x)=0 с точностью
5.	Аналогично п. 1-4 попытаться найти корни уравнения g(x)=0. Объяснить полученные результаты.

Теоретический материал:

Метод деления отрезка пополам (метод бисекции) на первом шаге локализует корень функции f(x) на определенном отрезке [a,b], где f(a)*f(b)<0 (1)

далее этот отрезок делится пополам и для следующей итерации выбирается половина, где опять выполняется условие (1), т.е. функция пересекает ось абсцисс.

Итерационный процесс останавливается, когда длина очередного отрезка [a,b] станет меньше либо равна половине заданной заранее точности e. Ответом будет середина отрезка [a,b].

Исходные данные:

с

ε .

4		10	2		4	2
f(x) := x	-	3	× x	+ 1	g(x) := x	- 6 × x	+ 9

Аналитическое решение задачи:

ORIGIN := 1

solve_square_ur(a,b, c)

a_f := 1 b_f := -310

:=	D ¬ b2 - 4 × a × c
	return 0		if	D < 0
		-b -
	X1 ¬				D
			2 × a
		-b +
	X2 ¬				D
			2 × a
	X
c_f := 1

X1_f := - 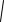solve_square_ur(a_f, b_f, c_f)2

X2_f := - 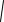solve_square_ur(a_f, b_f, c_f)1

X3_f := 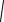solve_square_ur(a_f, b_f, c_f)1

X4_f := solve_square_ur(a_f, b_f, c_f)2

a_g := 1 b_g := -6 c_g := 9

X1_g := -			solve_square_ur(a_g, b_g,c_g)2
X2_g := -
			solve_square_ur(a_g, b_g,c_g)1
X3_g :=
		solve_square_ur(a_g, b_g,c_g)1
X4_g :=
		solve_square_ur(a_g, b_g,c_g)2

X1_f = -1.732050808		X1_g = -1.732050808
X2_f = -0.577350269		X2_g = -1.732050808
X3_f = 0.577350269	Четыре корня	X3_g = 1.732050808	Два корня
X4_f = 1.732050808		X4_g = 1.732050808

Локализуем корни уравнений f(x)=0, g(x)=0 графически 0<x<2:

3.7

10

7.5

2.3

g(x) 5

f(x) 0.9

2.5

0.5

0

0.5

1

1.5

2

1.9

0

0.5

1

1.5

2

x

x

Решение задачи итерационным методом:

Bisec(f, a,b, e) :=

an ¬ a

bn ¬ b

k ¬ 0

while (bn - an) > 2 × e

xn ¬ an + bn

2

fa ¬ f(an)

fb ¬ f(bn)

fxn ¬ f(xn)

bn ¬ xn

if

fa × fxn £ 0

an ¬ xn

otherwise

k ¬ k + 1

xn ¬ an + bn

2

res ¬

æxn ö

ç

÷

è

k ø

res

Проверка решения средствами MathCAD:

e := 10− 10

TOL := e

Первый корень f(x)=0:

Bisec(f, 0.5, 2,e) =

æ0.577350269 ö

x0 := 0.5

root(f(x0) , x0) = 0.577350269

è

33

ø

Второй корень f(x)=0:

Bisec(f, 1.5, 2,e) =

æ1.732050808 ö

x0 := 2

root(f(x0) , x0) = 1.732050808

è

32

ø

Первый корень g(x)=0:

æ	2	ö	x0 := -2
Bisec(g,1, 2,e) = ç	33	÷	root(g(x0), x0)	= -1.732053358
è		ø
Второй корень g(x)=0:
æ	2	ö	x0 := 2
Bisec(g,1, 2,e) = ç	33	÷	root(g(x0), x0)	= 1.732053358
è		ø

Вывод: В ходе решения нелинейных уравнений итерационными методами, их результаты

и результаты аналитического решения совпали в пределах верных цифр заданной точности, что подтверждает правильность работы алгоритмов. При вычислении корня уравнения g(x)=0 алгоритм не сошелся к искомому корню. Это объясняется тем, что функция в окрестности данного корня имеет один и тот же знак, что

не позволяет итерационному алгоритму бисекции корректно выбрать один из полуотрезков.

Задача 3.2. Найти указанный в варианте корень уравнения f(x)=0 с точностью ε = 10−6 . Предварительно

графически локализовать корень. Написать программный модуль, реализующий метод Ньютона. Попытаться решить уравнение методом Ньютона при различных начальных приближениях, выбираемых как слева, так и справа от искомого корня, а также на различных расстояниях от него (рекомендуется рассмотреть 6-7 различных приближений). Проанализировать полученные результаты: сошелся ли итерационный процесс к искомому корню (хотя бы для одного начального приближения сходимость должна иметь место)? Если процесс не сошелся, то указать причины? Если сошелся, то какое количество итераций для этого потребовалось? Вывести и проанализировать таблицы, отражающие динамику сходимости (или расходимости, если она для каких-то начальных приближений имела место) последовательных

приближений {x(n) } для каждого варианта начальных приближений. Сделать выводы.

Теоретический материал:

В данной задаче нахождение корней с заданной точностью e на отрезках локализации производится при помощи метода Ньютона (метод касательных). Геометрически этот метод состоит в том, что наша дуга кривой y=f(x) заменяется касательной к этой кривой в точке x0(начальное приближение). Следующая касательная проводится в точке x1

,полученной в результате пересечения первой касательной с осью абсцисс и т.д. Именно

так и организуется итерационный процесс, в результате которого мы получаем ответ с
заданной точностью. Каждая последующая точка xn находится:
xn = xn−1 -	f(xn−1)
	f(xn−1)
d
dxn−1
Исходные данные:
f(x) := 2 × sin(x - 0.6) + x - 1.5
Решение задачи:
df(x) := d f(x)		df2(x) := d2 f(x)
	dx	dx2

Локализуем корни уравнения f(x)=0 графически:

												3.78
												2.55
f(x)												1.33
df(x)												0.1
				4		3		2		1					0			1		2		3		4
df2(x)												1.12
												2.35
												3.57
													4.8
														x

x0 := 1

root(f(x0) , x0) = 0.903079149706601

Newton(f,b, e) := x ← b x0 ← 0 i ← 1

while x − x0 > e x0 ← x

f(x0)

x ← x0 −

		d		f(x0)
	dx0
i ← i + 1
æ	x		ö
res ← ç	i − 1		÷
ç	x − x0		÷
è			ø

Произведем оценку динамики сходимости:

æ	0.90308		ö
ç			÷
Newton(f,0.6 ,10− 6) = ç	3		÷
ç	− 7		÷
è	9.65814 × 10		ø
æ	0.90308		ö
ç			÷
Newton(f,0.8 ,10− 6) = ç	3		÷
ç	− 8		÷
è	7.11082 × 10		ø
æ	0.90308	ö
ç		÷
Newton(f,1, 10− 6) = ç	3	÷
ç	− 7	÷
è1.44354 × 10		ø

æ	0.90308	ö
ç		÷
Newton(f,0.7 ,10− 6) = ç	3	÷
ç	− 7	÷
è	5.39574 × 10	ø
æ	0.90308	ö
ç		÷
Newton(f,0.9 ,10− 6) = ç	2	÷
ç	− 7	÷
è	9.65814 × 10	ø
æ	0.90308	ö
ç		÷
Newton(f,1.2 ,10− 6) = ç	4	÷
ç	− 11 ÷
è	6.46132 × 10	ø

æ		0.90308			ö	æ			0.90308	ö
ç					÷	ç				÷
Newton(f,1.5 ,10− 6) = ç		4			÷	Newton(f,2, 10− 6) = ç			5	÷
ç		− 8			÷	ç			− 9	÷
è		6.74158 × 10			ø	è			2.68842 × 10	ø
	Динамика сходимости метода Ньютона
	Начальное приближение				Количество итераций				Погрешность
	0.6					3			9.65814E-7
	0.7					3			5.39574E-7
	0.8					3			7.11082E-8
	0.9					2			9.65814E-7
	1					3			1.44354E-7
	1.2					4			6.46133E-11
	1.5					4			6.74158E-8
	2					5			2.68842E-9

Вывод: Исходя из данных численного эксперимента можно сделать вывод, что итерационный процесс сходится тем быстрее, чем ближе к корню взято начальное приближение. Сходимость наблюдалась при всех начальных приближениях, но при анализе динамики сходимости при выборе двух начальных приближений на одинаковом удалении от корня (0.6 и 1.2), скорость сходимости была выше там, где "неблагоприятный фактор" -

отрицательное значение амплитуды функции f(x)*f' ''(x) было меньше, что подверждает теоретические сведения об этом итерационном алгоритме.

Задача 3.3. Найти указанный в варианте корень уравнения f(x)=0 с точностью ε = 10−9 методом секущих. Для этого необходимо предварительно графически определить отрезок его локализации [a, b]. Написать программный модуль, реализующий метод секущих.

При помощи программы попытаться решить уравнение методом секущих для двух различных вариантов выбора начальных приближений:

а) x0 = a , x1 = a + 1000b - a ;

b) x0 = b , x1 = b - 1000b - a ;

Проанализировать полученные результаты: сошелся ли итерационный процесс к

искомому корню (хотя бы для одного начального приближения сходимость должна иметь место)? Если процесс не сошелся, то указать причины? Если сошелся, то какое количество итераций для этого потребовалось? Вывести и проанализировать таблицы, отражающие динамику сходимости (или расходимости, если в одном из п. a) или b) расходимость

имела место) последовательных приближений {x(n) } для каждого варианта начальных приближений. Сделать выводы.

Теоретический материал:

В данной задаче для уточнения корней с заданной точностью e на отрезках локализации используется метод секущих. Геометрически этот метод отличается от метода касательных(см. задание 2.2) лишь тем, что касательная в этом случае заменяется на секущую и на входе итерационного процесса появляется два значения( x0, x1). Причём

каждая последующая точка xn+1 находится:

hn × f(xn)

xn+1 = xn - f(xn + hn) - f(xn) , где hn = xn−1 - xn

При этом условие выхода определяется неравенством:

xn+1 - xn < e

Исходные данные:

f(x) := x5 - 2 sin(x) + 1

Решение задачи:

	df(x) := d f(x)	df2(x) :=	d2		f(x)
			dx2
	dx

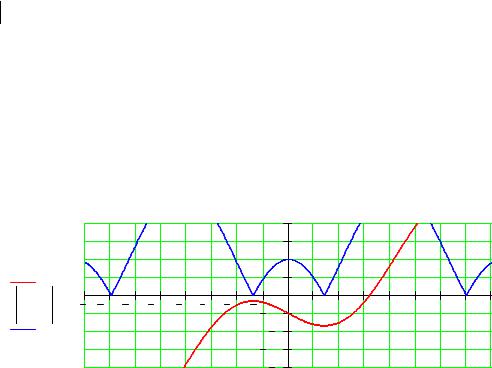
Локализуем корни уравнения f(x)=0 графически:

	10
	8.13
	6.25
f(x)	4.38
df(x)	2.5
df2(x)	0.63
1.5	1.13 0.75 0.38	0	0.38 0.75 1.13 1.5
	1.25

3.13

5

x

f(x)

1.5 1.36 1.22 1.08 0.94 0.8 0.66 0.52

df(x)

df2(x)

x0 := -1.13

root(f(x0) , x0) = -1.23639108

x

Cutline(x0,x1, e) := x1 ¬ x0

x2 ¬ x1

h2 ¬ x1 - x2 i ¬ 2

while xi - xi−1 ³ e

hi × f(xi) xi+1 ¬ xi - f(xi + hi) - f(xi)

i ¬ i + 1

hi ¬ xi−1 - xi

¬ æxi ö

res ç ÷

è i ø

Зададим отрезок локализации корня:

a := -1.5

b := -1.13

Первый вариант выбора начального приближения:

x0 := a	x1 := a +			b - a
				1000
	− 9	)	æ	-1.23639108 ö
Cutline(x0,x1, 10			= ç	9	÷
			è		ø

Второй вариант выбора начального приближения:

x0	:= b	x1 := b -				b - a
					1000
		− 9	)	æ	-1.23639108 ö
Cutline(x0,x1, 10				= ç	9			÷
				è				ø
x0	:= a
root(f(x0) , x0) = -1.23639108

Вывод: Данный итерационный метод аналогичен методу Ньютона и имеет те же самые рекомендации относительно выбора начального приближения.

В данном случае оба способа выбора начального приближения показали одинаковые результаты, но если принимать во внимание рекомендации для метода Ньютона, то первый способ выбора является наиболее оптимальным,

т.к. на отрезке начального приближения функция и её вторая производная имеют один и тот же знак.

Задача 3.4. Локализовать указанный корень уравнения f(x)=0 и найти его с точностью

ε = 10−7 , используя метод простой итерации. Для этого преобразовать уравнение f(x)=0 к виду x=ϕ(x), удобному для итераций. Проверить достаточное условие сходимости метода в выбранном отрезке локализации. Написать программный модуль, реализующий метод простой итерации. Использовать критерий окончания итерационного процесса вида

x(n+1) − x(n)

<

1− q

ε , где

q =

max

ϕ

′

(x)

,

q

x [a,b]

[a,b] - отрезок локализации для

искомого корня.

Указать количество выполненных

итераций. Вывести таблицу, отражающую динамику сходимости последовательных приближений {x( n) }.

Теоретический материал:

В данной задаче для нахождения корней с заданной точностью e используется метод простой итерации. Вначале уравнение f(x) = 0 преобразуется к виду x = f(x),удобному для итераций. Затем организуется итерационный процесс, где каждое значение xn+1 находится

следующим образом:

xn+1 = f(xn)

При этом условие выхода определяется неравенством:

x	- x		<	1 - q	× e	,где q = max|f'(x)| на отрезке локализации [a,b].
n+1	n			q

Исходные данные:

f(x) := x - sin(2 × x) - 0.5

Решение задачи:

Локализуем корни уравнения f(x)=0 графически:

		2
		1.5
	f(z)	1
		0.5
	d f(z)	3 2.63 2.25 1.88 1.5 1.13 0.75 0.38 0 0.38 0.75 1.13 1.5 1.88 2.25 2.63 3
	dz	0.5
		1

1.5

2

z

x := 1.5

root(f(x), x) = 1.190031

Как видно из вышепредставленного графика, на отрезке локализации корня не выполняется достаточное условие сходимости итерационного процесса, т.к на отрезке

локализации максимальное значение модуля производной функции имеет значение большее 1.

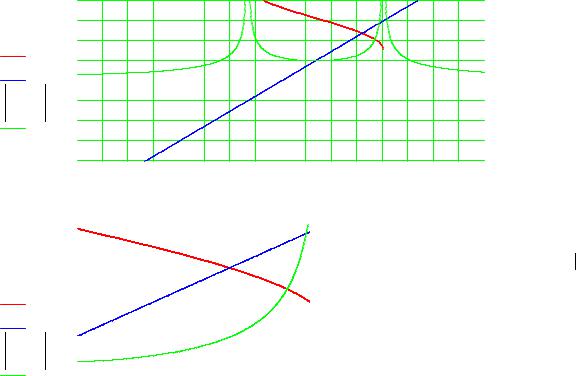
Для обеспечения сходимости итерационного процесса заменим уравнение f(x)=0 эквивалентным ему x=φ(x) таким образом, чтобы на отрезке локализации корня максимальное значение модуля производной функции φ(x) было меньше 1.

f(x) := 0.5 asin(0.5 - x) + p2

φ(z)

z

d φ(z) dz

φ(z)

z

d φ(z) dz

																																			2
																																			1.5
																																			1
																																			0.5
		3		2.63					2.25					1.88						1.5		1.13					0.75					0.38										0		0.38 0.75 1.13								1.5			1.88 2.25 2.63									3
																																					0.5
																																							1
																																					1.5
																																							2
																																										z
1.5																																																			df(x) := d f(x)
																																																															absdf(x) :=		df(x)
1																																																			x := 1						dx
																																																			Given									x ³ 0.7
0.5																																																												x £ 1.34
																																																			q := absdf(Maximize(absdf, x))
																																																			q = 0.921512
0.7			0.79						0.89						0.98					1.08				1.17						1.26										1.36				1.45

z

После замены исходного уравнения эквивалентным, максимальное значение модуля производной функции, передаваемой на вход алгоритма простой итерации, стало меньше 1 (q= 0.921512), что гарантирует сходимость итерационного процесса к решению.