Лекции Дудорова(Оптимизация.) / lection_dudarov / Лекция 8

5

Лекция 8

Решение обыкновенных дифференциальных уравнений

Решением дифференциального уравнения (ДУ) является некоторая функциональная зависимость y=y(x), которая при подстановке в уравнение обращает его в тождество.

Формы записи ДУ: F(x, y, y')=0;

y'=f(x, y).

Из высшей математики: .

Общее решение ДУ n-го порядка записывается в виде , где C₁, C₂, ..., C_n – константы.

Для нахождения частного вида решения ДУ необходимо иметь начальные условия y₀=y(x₀).

Решение ДУ численными методами получается в графической или табличной форме. Среди численных методов решения ДУ рассмотрим следующие:

1. метод Эйлера;

2. метод Эйлера модифицированный;

3. метод Эйлера-Коши;

4. метод Рунге-Кутта.

Решение задачи методом Эйлера показано далее.

Дано:

дифференциальное уравнение y'=f(x, y);

начальные условия y₀=y(x₀);

интервал интегрирования [x₀, x_к];

число искомых значений функции (число точек) n.

Найти:

y=y(x).

Шаг интегрирования определяем по соотношению (1):

. (1)

Исходное ДУ перепишем в виде:

. (2)

При достаточно большом количестве искомых значений функции (n) шаг интегрирования (h) будет достаточно мал. Используя допущение , перепишем (2) следующим образом:

. (3)

Отсюда получим рекуррентные соотношения для расчёта пар значений x и y исходного дифференциального уравнения:

(4)

Графическая интерпретация метода Эйлера представлена на рис. 1. На каждом шаге интегрирования через полученную на предыдущем шаге точку проводится касательная к функции y=y(x) до пересечения с координатой x на следующем шаге интегрирования. Точка, полученная пересечением касательной и вертикальной координатной прямой, является следующей на графике.

Рис. 1. Графическая иллюстрация метода Эйлера.

Главным недостатком метода является накопление ошибки интегрирования на каждом шаге. Уменьшить ошибку можно за счёт уменьшения шага интегрирования, что потребует, однако, более длительных вычислений.

Задание 1. Дифференциальное уравнения вида решить методом Эйлера на интервале [0, 5] с шагом 0,5 при начальном условии y(0)=1. Решив то же самое уравнение аналитически, проверить точность решения, полученного численно.

Аналитическое решение уравнения имеет вид: y*=F(x, y)+C, где F(x, y) – первообразная функции f(x, y), C – константа. В результате вычислений получаем .

Численное решение и сравнение результатов представлены в табл. 1.

Таблица 1

Результаты решения дифференциального уравнения методом Эйлера

xi	f(xi–1, yi–1)	yi	yi*	|yi|
0,0	–	1,00	1	0,00
0,5	–3,00	–0,50	–0,54	0,04
1,0	–3,13	–2,06	–2,08	0,02
1,5	–3,00	–3,56	–3,50	0,06
2,0	–2,63	–4,88	–4,67	0,21
2,5	–2,00	–5,88	–5,46	0,42
3,0	–1,13	–6,44	–5,75	0,69
3,5	0,00	–6,44	–5,42	1,02
4,0	1,38	–5,75	–4,33	1,42
4,5	3,00	–4,25	–2,38	1,88
5,0	4,88	–1,81	0,58	2,40

Модифицированный метод Эйлера позволяет устранить недостаток, связанный с накоплением ошибки интегрирования. Графическая иллюстрация работы метода представлена на рис. 2.

Рис. 2. Графическая иллюстрация работы модифицированного метода Эйлера.

На i-ом шаге интегрирования в точке x_i проводится касательная (1) к графику y=y(x) до пересечения с промежуточной прямой x=x_i+h/2. В промежуточной точке рассчитываются новые значения функции и её производной по методу Эйлера и строится новая касательная (2). Следующее рассчитанное значение функции получается при пересечении прямой (3), параллельной промежуточной касательной и проведённой через предыдущую точку графика (x_i, y_i), и вертикальной координатной прямой x=x_i+1.

Рекуррентные соотношения для определения координат точек на каждом шаге интегрирования следующие:

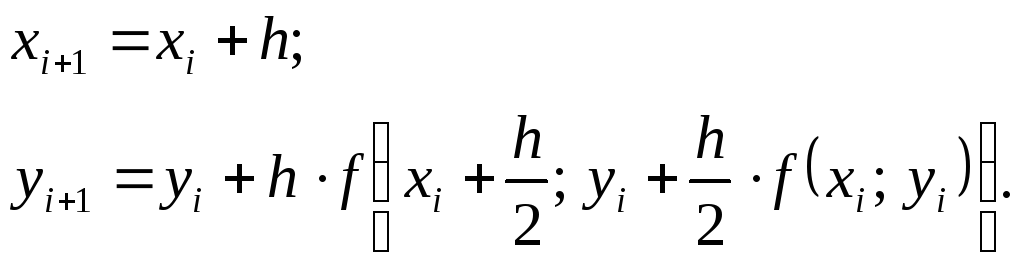(5)

Метод Эйлера-Коши также позволяет устранить недостаток простого метода Эйлера, связанный с накоплением ошибки интегрирования. Графическая иллюстрация работы данного метода представлена на рис. 3.

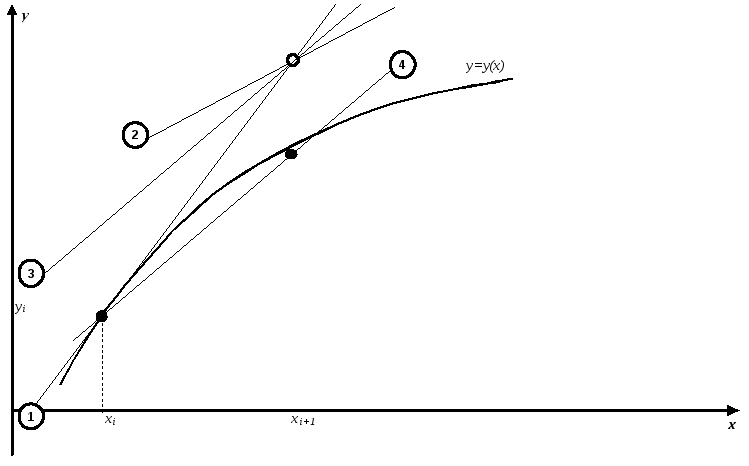
Рис. 3. Графическая иллюстрация работы метода Эйлера-Коши.

На i-ом шаге интегрирования в точке x_i проводится касательная (1) к графику y=y(x) до пересечения с прямой x=x_i+1. В точке x_i+1 рассчитывается новое значение функции y(x_i+1) и по методу Эйлера и строится новая касательная (2). В той же точке x_i+1 строится ещё одна прямая (3), угол наклона которой есть среднее арифметическое углов наклона двух первых прямых. Через точку x_i проводится прямая (4), параллельная прямой с усреднённым углом наклона, до пересечения с прямой x=x_i+1. Последняя точка пересечения и есть новая точка графика искомой функции.

Рекуррентные соотношения для определения координат точек на каждом шаге интегрирования следующие:

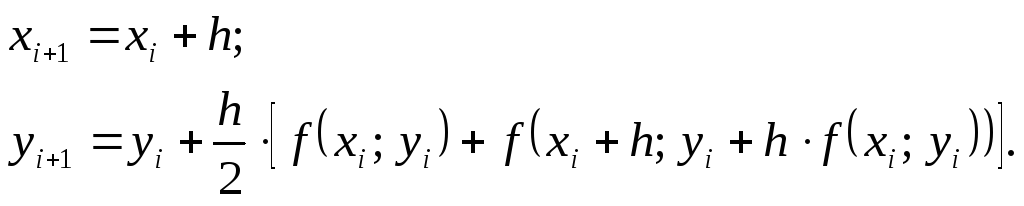(6)

Более сложные методы основаны на большем количестве промежуточных построений. Одним из таких методов является метод Рунге-Кутта 4-го порядка. Порядок метода как раз и обусловлен числом промежуточных касательных. Формализация рекуррентных соотношений для расчёта координат точек графика искомой функции на каждом шаге интегрирования методом Рунге-Кутта 4-го порядка представлена ниже.

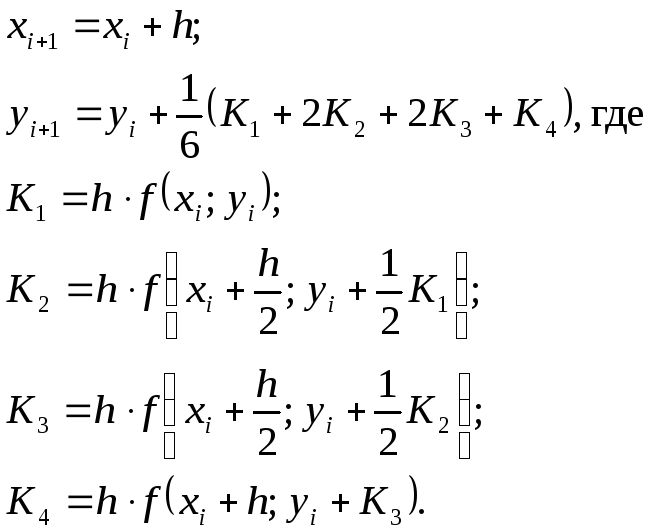(7)