Лекции Дудорова(Оптимизация.) / lection_dudarov / Лекция 11

Лекция 11

Оптимизация методами детерминированного поиска.

Методы оптимизации функции нескольких переменных

К детерминированным методам поиска точки экстремума функции нескольких переменных относятся:

• метод поочерёдного изменения переменных (Гаусса-Зейделя);

• метод сканирования;

• симплексный метод.

Алгоритм метода поочерёдного изменения переменных следующий.

1. Задаётся начальное приближение x⁽⁰⁾ с координатами (x₁⁰, x₂⁰).

2. Последовательно вычисляются значения целевой функции вдоль одной из координат, пока целевая функция улучшается.

3. Последовательно вычисляются значения целевой функции вдоль другой координаты, и так для всех координат. На каждом этапе 2, 3 выбирается шаг изменения переменных.

4. Пункты 2, 3 повторяются до достижения заданной точности по x:

,

где n – размерность задачи (количество переменных).

Задание 1. Найти минимум функции традиционным методом и методом поочерёдного изменения переменных с начальной точкой (0, 0) и начальным шагом изменения переменных 0,4.

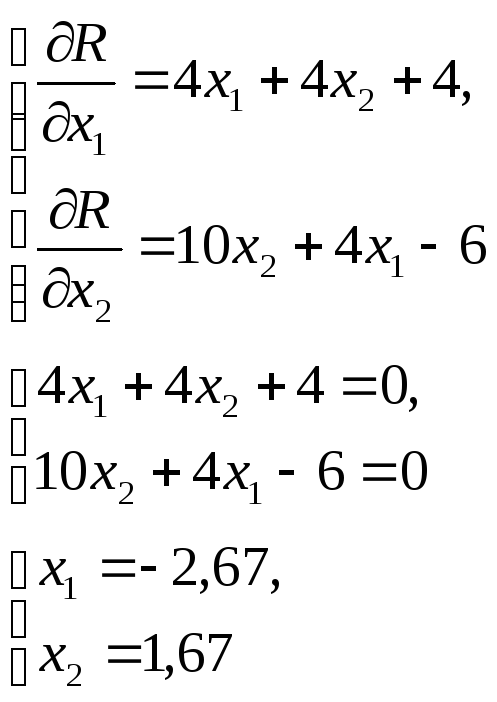
0	0	8	шаг 0,4
0,4	0	9,92
-0,4	0	6,72
-0,8	0	6,08
-1,2	0	6,08
-0,8	0,4	3,2
-0,8	0,8	1,92
-0,8	1,2	2,24
-1	0,8	1,2	шаг 0,2
-1,2	0,8	0,64
-1,4	0,8	0,24
-1,6	0,8	0
-1,8	0,8	-0,08
-2	0,8	0
-1,8	1	-0,92
-1,8	1,2	-1,36
-1,8	1,4	-1,4
-1,8	1,6	-1,04
-1,9	1,4	-1,62	шаг 0,1
-2	1,4	-1,8
-2,1	1,4	-1,94
-2,2	1,4	-2,04
-2,3	1,4	-2,1
-2,4	1,4	-2,12
-2,5	1,4	-2,1
-2,4	1,5	-2,23
-2,4	1,6	-2,24
-2,4	1,7	-2,15
-2,45	1,6	-2,275	шаг 0,05
-2,5	1,6	-2,3
-2,55	1,6	-2,315
-2,6	1,6	-2,32
-2,65	1,6	-2,315
-2,6	1,65	-2,3275
-2,6	1,7	-2,31

Алгоритм метода сканирования следующий.

Дано: целевая функция R(x₁, x₂) определена на интервалах [x₁^н, x₁^к]U[x₂^н, x₂^к].  – точность решения задачи.

1. Исходные интервалы изменения переменных разбиваются на p_j подынтервалов (j=1..n) с длиной

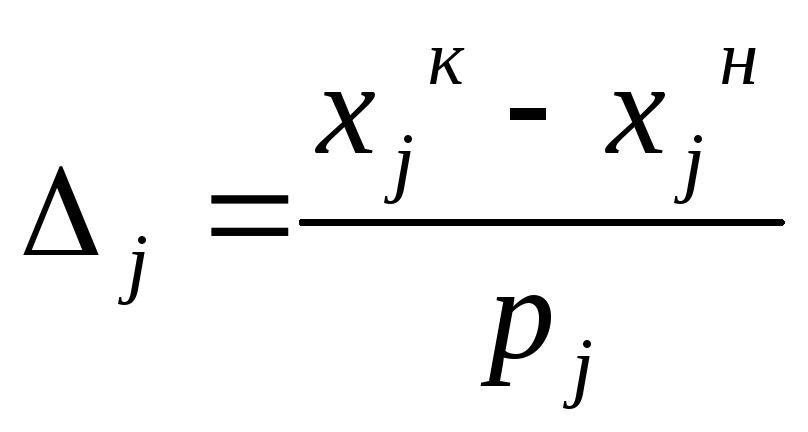
или на одинаковое количество подынтервалов p_j=p для всех j=1..n.

2. Во всех узловых точках рассчитывается значение целевой функции и определяется точка, имеющая наилучшее значение критерия оптимальности R(x_opt).

3. Процедура п./п. 1, 2 повторяется в пределах новых границ:

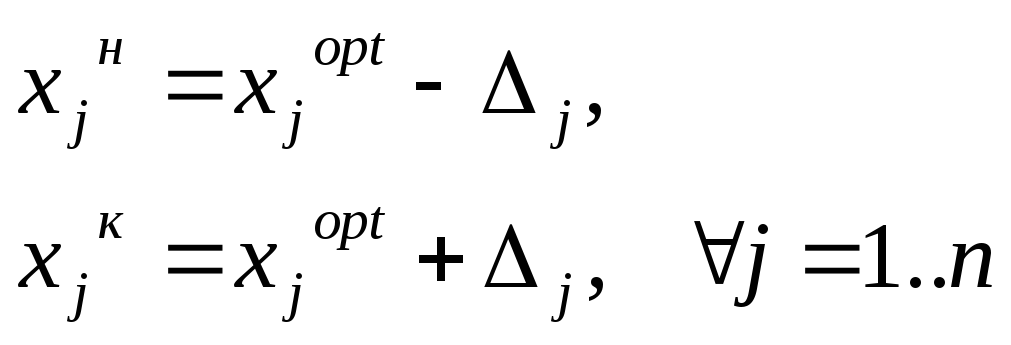
4. Условие окончания вычислений: j<= для всех j=1..n.

Выбор начального шага сканирования (числа подынтервалов на первом этапе расчёта) может иметь большое значение. При большом шаге можно пропустить глобальный оптимум между узлами сетки. В то же время, при малом шаге требуется большой объём вычислений.

Одна из модификаций данного метода – сканирование по спирали. Положение оптимума уточняется при переносе центра сканирования в определённую на предыдущем этапе точку оптимума и уменьшении приращения радиуса витка. Если при очередном витке спирали лучшее значение целевой функции не найдено, оптимум должен находиться внутри данного витка.

Данная модификация метода эффективна только для случая функции двух переменных.

Симплексный метод.

Симплексом в n-мерном пространстве является многогранник, имеющий n+1 вершину, каждая из которых определяется пересечением n гиперплоскостей данного пространства.

Для случая двух переменных симплекс – треугольник, трёх переменных – четырёхгранная пирамида.

Алгоритм метода для случая двух переменных следующий.

1. Строится начальный симплекс: задаются три точки в пространстве переменных целевой функции, образующие равносторонний треугольник.

2. Рассчитывается значение целевой функции в вершинах симплекса и определяется наихудшее из них.

3. Осуществляется симметрия наихудшей точки относительно противолежащей грани симплекса. В результате получаем новый симплекс из двух старых точек и одной новой.

4. Для новой точки рассчитывается значение целевой функции и определяется наихудшая точка из всех вершин нового симплекса.

5. Процедура п./п. 3, 4 повторяется до возникновения зацикливания вблизи оптимума. При возникновении зацикливания уменьшается размер симплекса: вместо симметричного преобразования уменьшается расстояние от наихудшей вершины до противолежащей грани.

6. Условие окончания: S_i<= для всех i=1..n+1, то есть все рёбра симплекса меньше или равны заданной точности.

Вершина нового симплекса определяется по соотношениям:

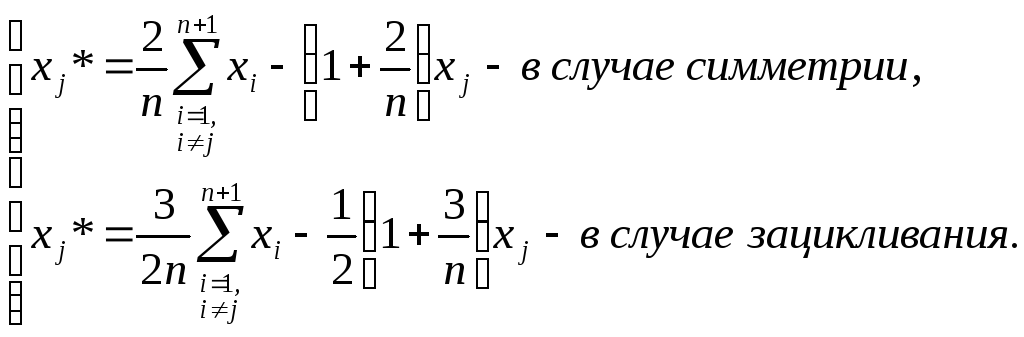
Интересной модификацией симплексного метода является метод деформируемых многогранников (метод Нелдера-Мида). Его отличие от предыдущего метода заключается в том, что если в случае симметричного отображения наихудшей точки новая точка даст наилучшее значение целевой функции, то делается попытка отобразить эту точку на расстояние, вдвое большее, чем было раньше. Если же значение в новой точке оказалось ещё хуже, делается попытка отобразить эту точку на расстояние, вдвое меньшее, чем было раньше.