Лабораторные работы / Отчеты / Решение уравнения с одним неизвестным - Епишкин - Вариант 15 - Михеев - 2006 / Ур-я с одним неизвестным
.docРоссийский химико-технологический университет им. Д.И.Менделеева
Кафедра вычислительной математики
ОТЧЕТ
РЕШЕНИЕ УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Вариант 15
Выполнил: Михеев Д.И.. гр. И-24
Проверил: Епишкин А.П.
Москва 2006
Дано уравнение
в виде
,
где
некоторая функция переменной
.
Число
называется
корнем или решением данного уравнения,
если при подстановке
в
уравнение последнее обращается в
тождество.
.
Число
называют
также нулем функции
.
В общем случае
уравнение может иметь одно или несколько
корней, как действительных, так и
комплексных. Нахождение действительных
корней с заданной точностью можно
разбить на два этапа. Сначала корни
отделяются, т.е. определяются отрезки,
которые содержат по одному корню
уравнения, а затем вычисляются с требуемой
точностью
.
Отделение корней уравнения
,
в области определения, непрерывной
функции
,
можно осуществлять несколькими способами:
-
Табулированием - составлением таблицы из равноотстоящих значений независимой переменной и соответствующих значений функции и определение отрезков в которых смежные значения функции имеют различные знаки и следовательно содержат нулевые значения функции.
-
Построением графика функции. Определение минимальных отрезков, включающих точки пересечения графика функции с осью 0x.
Уточнение корня
на отрезке
,
в котором локализован только один
корень, осуществляется итерационными
методами, в которых последовательно,
шаг за шагом, производится уточнение
начального приближения корня. Итерацией
называется совокупность вычислительных
операций, приводящих к новому приближенному
значению корня. Если каждое последующее
значение находится все ближе к точному
значению, говорят, что метод сходится.
В противном случае метод расходится.
Поэтому возникает необходимость
исследования сходимости итерационного
метода.
Общая итерационная формула вычисления очередного приближения имеет следующий вид
,
где
За начальное приближение
принимают
значение внутри заданного отрезка. Все
методы уточнения корней различаются
способами вычисления поправки
.
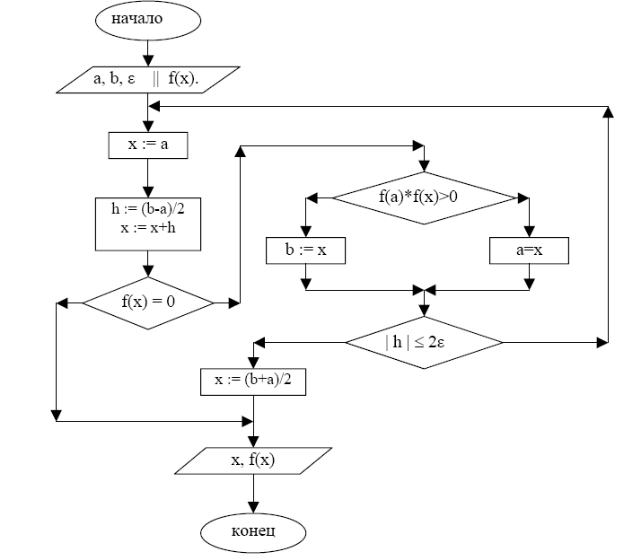
Метод половинного деления.
В этом методе на каждой итерации отрезок содержащий корень делится пополам и за новый отрезок для уточнения принимается одна из половин.
Алгоритм:
1. Задаем функцию
,
отрезок
и точность
.
2. За начальное
приближение принимаем левую границу
отрезка
,
т.е.
3. Вычисляем
поправку
и
новое приближение
4. Если
,
то
– корень.
5. В противном
случае, определяем новый отрезок
.
Проверяем, если
,
то
и
,
иначе
,
то
и
.
Далее проверяем условие окончания,
если
,
то за ответ принимаем значение равное
и переходим на пункт 6, иначе переходим
на пункт 2.
6. Выводим
и
.
Блок-схема:
Метод Ньютона или касательных.
В этом методе,
на каждой итерации, за новое приближение
к корню
принимается
точка пересечения касательной к графику,
построенной в точке
с осью
.
За начальное приближение к корню
принимаем
одну из границ отрезка
,
содержащего один корень. Если новое
приближение выходит за границы интервала,
то надо выбрать новое начальное
приближение и если это не помогает надо
попробовать уменьшить отрезок поиска
в два раза и повторить поиск методом
Ньютона.
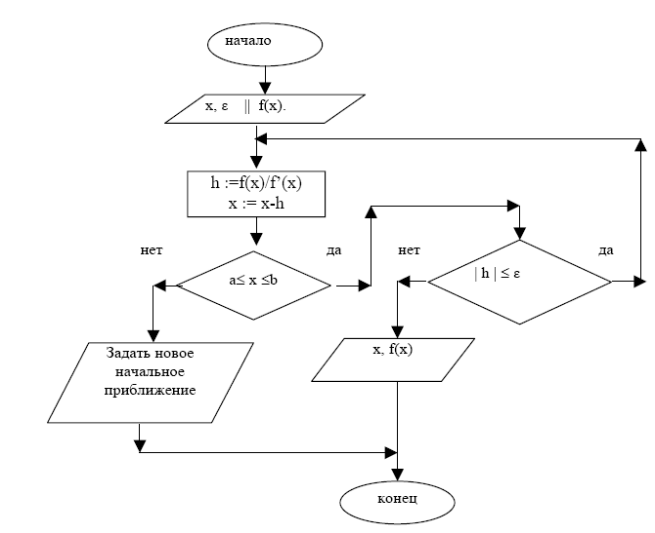
Алгоритм.
1. Задаем функцию
,
отрезок
и точность
.
За начальное приближение
принимаем одну из границ заданного
отрезка
.
2. Вычисляем
приращение значение шага
,
как
и новое
приближение, как
.
3. Проверяем
если
,
то
и повторяем с пункта 2.
4. Иначе проверяем
условие окончания, если
,
то выводим последнее значение
и
.
Иначе перейдем на пункт 2
Блок-схема
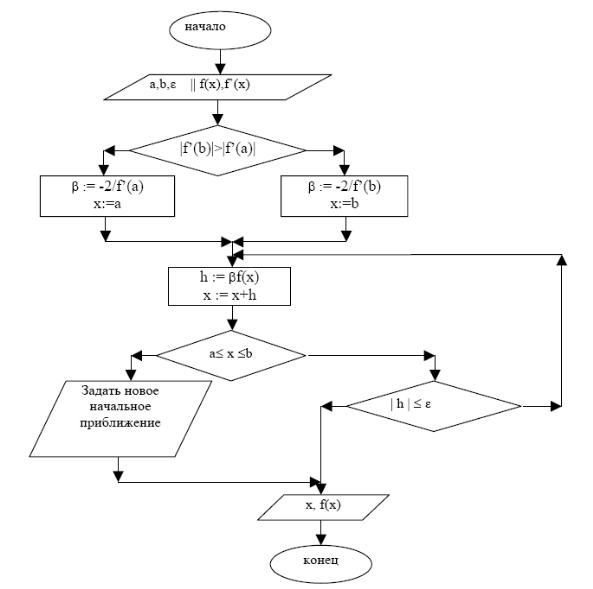
Метод простых итераций.
Пусть задано
нелинейное уравнение
и отрезок
,
который включает корень данного
уравнения, т.е.
и точность
,
с которой требуется уточнить значения
корня.
Преобразуем
исходное уравнение к эквивалентному
виду
.
Последовательность
будем называть итерационной, где
выражается
через элемент
по
рекуррентной формуле
,
т.е.
,
,
за
принимают
любое число на заданном отрезке
.
Говорят, что итерационный метод сходится,
если последовательность
имеет предел при
.
Для определения условия сходимости
определим
и применим теорему о среднем, тогда
.
Необходимо чтобы модуль разности
был меньше чем
,
а это справедливо только при
,
т.е. максимальная
производная на
заданном отрезке должна быть меньше
единицы. Так для решения квадратного
уравнения
можно положить
или
и соответствующие итерационные формулы
будут иметь вид
и
.
В первом случае метод не сходится, а во
втором сходится.
Общий подход
для получения итерационной формулы
:
помножим обе части уравнения на множитель
,
получим
и прибавим к обеим частям по
.
Окончательная итерационная формула
будет иметь вид
.
Функция:
;
ее производная:
;
;
;
.
Мы должны выбрать
максимальную по модулю производную на
заданном отрезке. Тогда, если
,
то
,
иначе
.
Блок-схема:
Программа по методу половинного деления
Option Explicit
Function F(X As Single) As Single
F = -33,065 – 2,823 * X + 5,425 * X ^ 2 + X ^ 3
End Function
Sub MPD ()
Dim c!, F1!, F2!, X1!, X2!, a!, b!, e!, i%
a = Cells (1, 2)
b = Cells (2, 2)
e = Cells (3, 2)
X1 = a
X2 = b
i = 0
Do Until X2 - X1 <= e
c = (X2 + X1) / 2
F1 = F(X1)
F2 = F(c)
If F1 * F2 < 0 Then
X2 = c
Else
X1 = c
End If
i = i + 1
Loop
Cells (5, 2) = "X ="
Cells (5, 3) = (X2 + X1) / 2
Cells (6, 2) = "F(X) ="
Cells (6, 3) = F(c)
Cells (7, 2) = "i ="
Cells (7, 3) = i
End Sub
Ответ:
на отрезке [-2.5;-2]
на отрезке [3; 3.5]
на отрезке [4; 4.5]
Программа по методу Ньютона или касательных
Option Explicit
Function F(X As Single) As Single
F = -33,065 – 2,823 * X + 5,425 * X ^ 2 + X ^ 3
End Function
Function F1(X As Single, dx As Single) As Single
F1 = (F(X + dx) - F(X)) / dx
End Function
Sub Kasat()
Dim h!, X!, X_next!, a!, b!, e!, i%, dx!
a = Cells (1, 2)
b = Cells (2, 2)
e = Cells (3, 2)
dx = Cells (4, 2)
i = 0
If F (a) > 0 Then
X_next = a
Else
X_next = b
End If
Do
X = X_next
h = -F(X) / F1(X, dx)
X_next = X + h
i = i + 1
Loop Until Abs(X - X_next) < = e
Cells (5, 2) = "X ="
Cells (5, 3) = X_next
Cells (6, 2) = "F(X) ="
Cells (6, 3) = F (X_next)
Cells (7, 2) = "i="
Cells (7, 3) = i
End Sub
Ответ:
на отрезке [-2.5; -2]
на отрезке [3; 3.5]
на отрезке [4; 4.5]