Дискретка / 3 - Отношения

3. Отношения

Основные понятия и определения

Бинарное отношение, заданное на (во) множестве A, – это некоторый признак связывающий пары элементов из A. В этом случае используется запись: xRy, это читается: «элемент x находится в отношении R с y».

Кроме того, поскольку бинарное отношение R описывает некоторые внутренние связи между элементами множества A, то связанные этим отношением элементы можно

представлять как упорядоченные пары (x, y), где

x, y A, и множество таких

упорядоченных пар будет представлять собой некоторое подмножество R декартова квадрата A2. В этом случае (если понимать бинарное отношение как подмножество

декартова квадрата) связь элемента	x A	отношением R с	y A	будем записывать, как
x, y R .

	Примеры.
1)	Отношение равенства действительных чисел определяется на множестве
A ; следующим образом:
	x, y ; : xRy x y .
2)	Отношение строгого (R1) и нестрогого (R2) неравенства действительных чисел
задается на множестве A ; следующим образом:
	x, y ; : xRy x y ;
	x, y ; : xRy x y .

3) Отношение неравенства кортежей с действительными координатами (неравенство

Парето) определяется на множестве	A R	n			n	следующим образом:
			;
x, y ; n	: xRy i				xi	yi .
				1, n

Здесь R – неравенство кортежей, x = (x1, …, xn) и y = (y1, …, yn) – кортежи длины n с действительными координатами, т.е. xi, yi, i 1, n , – действительные числа.

Это отношение часто обозначают символом или ≤ (но второй не следует путать с

неравенством действительных чисел).

4)

Лексикографическое неравенство кортежей, имеющее стандартное обозначение

или < (второе не следует путать со строгим неравенством действительных чисел):

x, y ;

n

: xRy k 1, n x

y

& i 1, k 1 x

y

.

k

k

i

i

5)

Отношение неравенства функций.

f , g C

a,b

: fRg x a, b f x g x .

Здесь A = C[a, b] – множество действительных функций, непрерывных на отрезке [a, b].

6)

Отношение равенства по модулю 5.

Пусть A = Z – множество целых чисел. Бинарное отношение R равенства по модулю

5 определим следующим образом:

m, n Z : mRn r5 m r5 n ,

где r5(n) – остаток от деления числа n на 5, т.е. фактически R – признак (отношение) равенства остатков при делении на 5. Это отношение записывается m ≡ n (mod 5) или

mod 5

m n .

1

Очевидно, что r5(m) = r5(n) тогда и только тогда, когда число m – n делится на 5 без

остатка, т.е.

k Z : m n 5k , что означает, что равны по модулю 5 все числа, разность

между которыми кратна пяти. Это, к примеру, числа 1 ≡ 6 ≡ 11 (mod 5), 3 ≡ 8 ≡ 13 (mod 5). Подобным образом можно определить отношения равенства по произвольному

модулю p N . При p = 1 получаем обычное отношение равенства		чисел.	При p 1
данное отношение определяется следующим образом:
m, n Z : m n mod p k Z m n pk .			□
Свойства бинарных отношений
1°.Рефлексивность:	a A: aRa ;	A	R
	a, a R.
Это означает, что диагональ декартова квадрата A2 содержится		во	A
множестве R (см. рис. 7).			Рис. 7
2°.Антирефлексивность:	a A: aRa ;
	a, a R.	A	R
Это означает, что ни одна точка диагонали декартова квадрата A2 не			A
принадлежит множеству R (см. рис. 8).
			Рис. 8
	a,b A : aRb bRa ;
3°.Симметричность:

		a,b R b, a R ,
т.е. множество R симметрично относительно диагонали декартова
квадрата A2 (см. рис. 9).
4°.Антисимметричность:	a,b A :	aRb & bRa a b;
		a,b R & b, a R a b,

т.е. во множестве R нет ни одной пары симметричных точек вне диагонали декартова квадрата A2 (см. рис. 10).

5°.Транзитивность:	a,b, c A : aRb & bRc aRc ;
	a,b R & b, a R a, c R ,

т.е. движение, показанное на рис. 11 стрелками, не выводит за пределы множества R.

6°.Антитранзитивность:	a,b, c A : aRb & bRc aRc ;
	a,b R & b, a R a, c R.
7°.Полнота (связность):	a,b A : a b aRb bRa ;

A R

A

Рис. 9

A R

A

Рис. 10

c A

b

b A a

Рис. 11

a b a,b R b, a R , т.е. любая точка вне диагонали либо сама принадлежит множеству R, A либо симметричная ей точка является элементом R. Пример полного отношения приведён на рис. 12.

Если на множестве A задано бинарное отношение R и

рассматривается некоторое B A , то отношение

RB a, b : a, b B & aRb R B2

называется сужением отношения R на подмножество B.

Сужение может обладать иными свойствами, нежели само отношение, которого оно задано.

R

A

Рис. 12

на основе

2

Пример 1.

Рассмотрим строгое неравенство действительных чисел (1) и проверим для него наличие описанных свойств.

1°.Рефлексивность: x ; : x x .

Полученное утверждение является ложным, значит, рассматриваемое отношение не является рефлексивным.

2°.Антирефлексивность: x ; : x x .

Высказывание в скобках является ложным для любого x, поэтому всё утверждение оказывается истинным, т.е. отношение строгого неравенства действительных чисел

является антирефлексивным.	(+)
3°.Симметричность: x, y ; : x y y x .

При выполнении (И) первого неравенства второе всегда будет нарушаться (Л), и логическое следствие обратит всё утверждение в ложь ( И Л Л ). Таким образом, свойством симметричности рассматриваемое отношение не обладает.

4°.Антисимметричность: x, y ; : x y & y x x y .

Известно, что результат логического следствия может оказаться ложью только в случае, когда посылка является истинной, а следствие ложным. Однако для записанного предиката невозможно подобрать таких значений x и y, для которых одновременно выполнятся оба неравенства (и результатом конъюнкции будет истина), поэтому посылка всегда будет ложной, а значит, независимо от истинности (ложности) следствия, всё утверждение будет истинным ( Л Л И , Л И И ). А это означает антисимметричность бинарного отношения строгого неравенства

действительных чисел.	(+)
5°.Транзитивность: x, y, z ; : x y & y z x z .

Истинность данного утверждения очевидна, и рассматриваемое отношение

транзитивно.	(+)
6°.Антитранзитивность: x, y, z ; : x y & y z x z

	Ясно, что данное утверждение ложно, и свойством антитранзитивности
	рассматриваемое бинарное отношение не обладает.
					y
	7°.Полнота (связность): x, y ; : x y x y y x .
			R
	Истинность данного высказывания также очевидна,	а значит,
			0				x
	бинарное отношение строгого неравенства действительных чисел
	является полным.	(+)
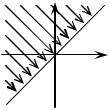
	Приведённый на рис. 13 график данного бинарного	отношения		Рис. 13
	также хорошо иллюстрирует наличие указанных свойств.						□

Отношение эквивалентности

Бинарное отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Пусть на множестве A задано отношение эквивалентности R. Тогда классом эквивалентности (смежности) элемента a A называется множество:

a | R b A : bRa ,

т.е. множество элементов, эквивалентных ему.

3

Два элемента множества будут эквивалентны тогда и только тогда, когда они принадлежат одному классу смежности.

Множество всех классов смежности множества A называется его фактор-

множеством и обозначается:

A | R a | R : a A .

Пример 2.

Заданное на множестве студентов факультета отношение принадлежности одной учебной группе, можно показать, является отношением эквивалентности. Классами эквивалентности при этом являются отдельные учебные группы, а фактор множеством – множество учебных групп факультета. □ Фактор-множества множества A является его разбиением на непустые классы, т.е.

имеет место Теорема. Эквивалентность, заданная на множестве, определяет некоторое разбиение

этого множества на классы эквивалентности.

	Обратная теорема. Любое разбиение Bi	: i I множества A на непустые классы
определяет некоторую эквивалентность R на множестве A.
	Например, отношениями эквивалентности являются:
отношение параллельности прямых на плоскости;
	отношения равенства целых чисел по модулю p ( p N );
отношение на множестве действительных чисел, задаваемое следующим образом:
	a, b R : aRb a b Q ;
	отношение тождества A a, a : a A	на любом множестве A, в частности,
отношение равенства действительных чисел;
отношение подобия геометрических фигур;
	отношение равномощности множеств.	□

Отношение порядка

Бинарное отношение R называется отношением порядка, или просто порядком, если оно антисимметрично и транзитивно.

Рефлексивный порядок называется нестрогим, антирефлексивный – строгим. Обозначаются они символами ≤ (или ) и < (или ) соответственно.

Множество, на котором задано отношение порядка, называется упорядоченным. Различают строго и нестрого упорядоченные множества. То, что множество A является упорядоченным с порядком R, обозначается (A, R). На одном множестве может быть задано несколько различных порядков, т.е. множество может быть упорядочено различными образами.

Пусть дано множество A с заданным на нём отношением порядка R. Тогда, если два элемента a, b A связаны между собой отношением R, т.е. aRb bRa , или, то же самое,

a, b R b, a R , то они называются сравнимыми, в противном случае элементы a и b

называются несравнимыми.

Отношения порядка также называют иногда отношениями предшествования, и, если aRb, то считается, что элемент a предшествует b или a не превосходит b, или b следует за элементом a.

4

Порядок называется линейным, или совершенным, если он является полным. Если же он свойством полноты не обладает, то он называется частичным.

Множества с установленным на нём отношением частичного или линейного порядка, называется, соответственно, частично или линейно упорядоченным.

Таким образом, в линейно упорядоченном множестве любая пара элементов сравнима, в частично же упорядоченном множестве есть несравнимые элементы.

Примеры.

1) Из примера 1 видно, что бинарное отношение строгого неравенства действительных чисел является строгим линейным порядком. Таким образом, множество действительных чисел может быть строго линейно упорядочено с помощью данного бинарного отношения.

2)	Отношение включения множеств, определённое на			2		, где		– произвольное
множество, т.е.
	A, B 2		: ARB A B ,
является частичным порядком.
3)	Отношение делимости натуральных чисел:
	m, n N : mRn m делит n ,

является частичным порядком.

4)Отношение неравенства кортежей является частичным порядком, т.к. существуют несравнимые кортежи.

5)Отношение лексикографического неравенства кортежей является линейным порядком, поскольку обладает свойством полноты. Докажем это. Для этого предположим, что x y , тогда, очевидно,

i 1, n : x	i		y	i	.
Обозначим:
k min i : x		i	y		.
				i

Это означает, что

x	k	y	& i 1, k 1: x	i	y	.
		k			i

Кроме того, x означает, что

k x



yk означает, y , а второго

что или

– что

y

xk < yk, или yk < xk. Выполнение первого неравенства

x , что и требовалось доказать.

□

5