Дискретка / 2 - Отображения

	2. Отображения
Отображение f множества A на (во) множество B – это правило, в соответствии с
которым элементам множества A ставятся в соответствие элементы множества B.
Обозначается: f: A → B.
Элемент из множества B,	соответствующий a A , называется его образом при
отображении f. Множество образов элемента a обозначается f (a) или Ba.
Элементы же множества	A, которым соответствует	b B , называются его

прообразами при отображении f и обозначаются ab ( ab

: b f ab ). Множество прообразов

элемента b обозначается Ab.

Отображение

f–1: B → A называется

обратным к

отношению

f,

если b B :

f

1

b Ab .

Если

для

каждого

элемента множества

A

существует

его

образ,

т.е.

a A : f a ,

то отображение f называется полным, или всюду определённым. Иначе

(если a A : f a ) отображение называется частичным.

Множество всех элементов из A, имеющих образы, называется областью

определения отображения и обозначается:

D

f

D f a A : f a .

Ясно, что для полного отображения Df = A. Если же отображение f – частичное,

D f

A & D f

A , т.е. Df является собственным подмножеством множества A.

Множество всех элементов B, имеющих прообразы, называется множеством

образов (областью значений) отображения f и обозначается:

Im

f

Im f R f b B : a A b f a .

Отображение называется однозначным (функцией), если каждый элемент множества

A содержит не более одного образа, т.е.

a A :

f a

1 ,

где

f a

– число образов

элемента a.

В противном случае (если

a A : f a 1),

отображение

f называется

многозначным.

Если образ множества A совпадает с множеством B, т.е. Imf = B, или, то же самое,

b B a A : b f a , то отображение f: A → B называют отображением A на множество

B и пишут f

: A B .

на

Если же в B есть элементы, не имеющие прообразов,

т.е.

b B a A : b

f a ,

или, то же самое, Im f

B & Im f B , то отображение f : A → B называется отображением

в

множества A во множество B и обозначается f : A B .

Если отображение f является однозначным (функциональным) всюду определённым отношением множества A на B, то его называют сюръективным (сюръекцией).

Если при некотором однозначном отображении каждый элемент области значений имеет единственный прообраз, т.е. из f (a1) = f (a2) следует a1 = a2, то такое отображение называется инъективным (инъекцией).

Если отображение является инъекцией и сюръекцией одновременно, то оно называется биекцией, или взаимнооднозначным отображением (функцией). При этом обратное отображение также является взаимнооднозначной функцией.

Схематично различные типы отображений представлены в виде диаграмм на рис. 5.

1

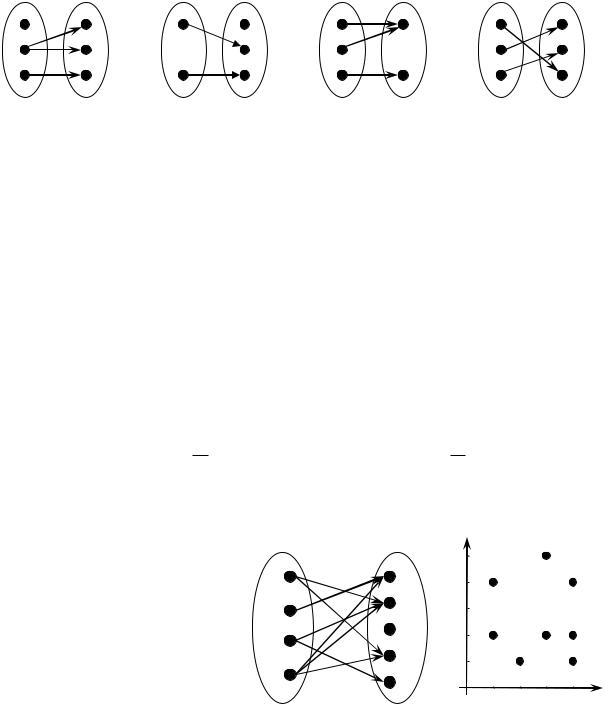
A B A B A B A B

отношение, но	инъекция, но	сюръекция, но	биекция
не функция	не сюръекция	не инъекция
		Рис. 5

Отображения конечных множеств бывает удобно задавать с помощью таблиц, в которых указываются все элементы первого множества и соответствующие им образы – элементы второго множества, или с помощью диаграмм. Кроме того, очевидно, что

каждое	отображение однозначно определяет множество упорядоченных	пар
x, y :	x A, y B , y f x , являющееся подмножеством декартова квадрата	A × B,

называемое графиком отображения f. Таким образом, отображения также могут быть заданы, как подмножества декартова произведения A × B.

Пример 1.

Пусть отображение f: A → B, где A = {a1, …, a4}, B = {b1, …, b5}, задано таблицей, представленной на рис. 6.а.

Отображение, обратное к f, также может быть задано таблицей (см. рис. 6.б). Диаграмма отображения f представлена на рис. 6.в. Она представляет собой

двудольный ориентированный граф, долями которого являются множества A и B, а дуги –

выходят из вершин ai A , i 1,4

, и заходят в вершины b j

B ,

j 1,5 .

График отображения f представлен на рис. 6.г. Каждая точка этого графика с

координатами (ai, bj) соответствует дуге (ai, bj) графа отображения f.
							A	B
a	f (a)		b	f	–1	(b)			b5
							f	b1
a1	{b2, b4}		b1	{a2, a4}
							a1		b4
a2	{b1}		b2	{a1, a3, a4}			a2	b2	b3
a3	{b2, b5}		b3				a3	b3	b2
a4	{b1, b2, b4}		b4	{a1, a4}				b4	b1
							a4
			b5		{a3}			b5	a1 a2 a3 a4
	а)			б)			в)		г)

Рис. 6

Видим, что f является полным отображением A в B, но не является функцией. Отображение f –1 представлялось бы аналогичной диаграммой с обратным направлением стрелок. Видим, что оно является частичным отображением B на A. Оба отображения, как f, так и f–1, являются многозначными. □

Пример 2.

Действительные функции являются частным случаем отображений. Рассматриваемые множества при этом являются бесконечными, поэтому для анализа таких отображений удобнее использовать их представления в виде графиков. Тогда несложно заключить, что, в частности,

2

а) y = ex – инъективна, но не сюръективна;
б) y = x3	– x – не инъективна, но сюръективна;
в) y = 2x + 1 – биективна;
г) y = x2	– не инъективна и не сюръективна.	□

Примечания.

Проверку свойств отображений можно проводить, заполняя таблицу следующего

вида:

Свойство			Отображения
	f1	f2		…	fn
Область
определения,
D(f)
Область
значений, Im(f)
полное /
частичное
на / в
однозначное /
многозначное
сюръекция
инъекция
биекция

3