Матем / 13

 

СТЕПЕННЫЕ РЯДЫ

 

1.     Определение степенного ряда.

2.     Радиус и интервал сходимости степенного ряда.

3.     Ряд Маклорена.

4.     Разложение функций в ряд Маклорена.

5.     Применение степенных рядов в приближенных вычислениях.

 

1.                              Определение степенного ряда.

Степенным рядом называется ряд вида:

а₀+а₁(х-а)+а₂(х-а)²+…+a_nxⁿ+…

где а - некоторое постоянное число, a₁,a₂,…,a_n- коэффициенты ряда,  n- целые неотрицательные числа.

Если а=0, то степенной ряд будет иметь вид:

a₀+a₁x+a₂x²+…+a_nxⁿ+…    (1).

Теорема Абеля: 1. Если степенной ряд сходится при некотором значении х₀, не равном 0, то он абсолютно сходится при всяком значении х, для которого.

2. Если степенной ряд расходится при некотором значении , то он расходится при любом х, для которого .

 

2.    Радиус и интервал сходимости степенного ряда.

Из теоремы Абеля следует, что если степенной ряд сходится при некотором значении х₀, то этот ряд абсолютно сходится в промежутке от     -х₀ до х₀, т.е. (-х₀;х₀).

Если при некотором значении  ряд расходится, то он расходится для всех х удовлетворяющих неравенствам, или  - интервалы расходимости.

Определение: Интервал (-R;+R), внутри которого степенной ряд сходится, называется интервалом сходимости ряда.

Половина интервала сходимости ряда называется радиусом сходимости: R - радиус сходимости.

На концах интервала   ряд может сходиться и расходиться.

Радиус сходимости определяется по формуле:

                (2)

Пример.  Определить  интервал  сходимости степенного ряда.

 

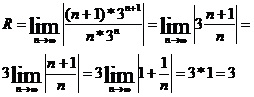
(-3;+3) - интервал сходимости. Исследуем  ряд на концах интервала:

При х=-3 получим знакочередующийся числовой ряд:

- условно сходится

При х=3 получим гармонический ряд

- расходится

Ответ:  интервал сходимости:  или х Ғ (-3;3).

 

3.      Ряд Маклорена.

, (3)

где,   .

Формула (3) называется формулой Маклорена.

Рядом Маклорена для функции f(x), о которой предполагается, что она определена в окрестности точки 0, и в этой точке имеет конечные производные любого порядка, называется степенной ряд:

  (4)

Функция f(x) будет суммой этого ряда только для тех значений х, при которых остаточный член (5) формулы Маклорена имеет своим пределом нуль, когда, т.е. когда   (5).

Ряд, стоящий в правой части формулы (4), называется рядом Маклорена для функции f(x), сама формула (4) дает разложение функции в ряд Маклорена.

 

 

4.      Разложение функций в ряд Маклорена.

1.                                      (6)

Формула верна при любом значении х.

2.                              (7)

Формула верна при любом значении х.

3.                               (8)

Формула верна при любом значении х.

4.                        (9)

Формула верна для значений х, удовлетворяющих условию 

5.

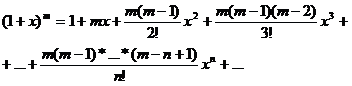
Формула верна для значений х, удовлетворяющих условию. Этот ряд называется биномиальным рядом.

 

5.   Применение степенных рядов в приближенных вычислениях.

Пример. Вычислить cos15⁰ с точностью до 0,00001.

радиан.

 

Погрешность

 

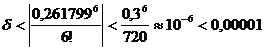
Пример.  Вычислить   с точностью   до 0,00001.

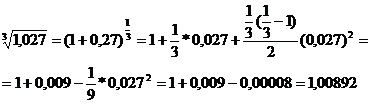
Полученный ряд знакочередующийся, поэтому величина погрешности не превосходит величины первого отброшенного члена.

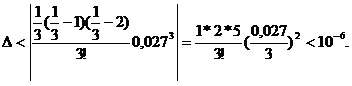
Пример.  Вычислить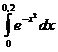 

Полученный ряд знакочередующийся, поэтому величина ошибки не превосходит величины отброшенного члена.