
Матем / 2
.docx|
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
1. Основные понятия и определения. 2. Метод Крамера для решения системы n линейных уравнений с n неизвестными. 3. Матричный метод для решения системы n линейных уравнений с n неизвестными. 4. Метод Жордана-Гаусса для решения системы n линейных уравнений с n неизвестными. 5. Теорема Кронекера-Капелли для исследования систем m линейных уравнений с n неизвестными. 6. Базисные и свободные переменные.
1. Основные понятия и определения. Система n линейных уравнений с n неизвестными имеет вид:
где аij (i=1, … n; j=1, …, n) – коэффициенты при неизвестных, вi – свободные члены, хj – неизвестные. Решением системы (1) называется такая совокупность n чисел, при подстановке которых каждое уравнение системы обращается в верное равенство. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. 2. Метод Крамера для решения системы n линейных уравнений с n неизвестными.
Теорема
Крамера.
Пусть ∆ - определитель
матрицы А, который называют главным
определителем системы,
а
Эти формулы называются формулами Крамера.
3. Матричный метод для решения системы n линейных уравнений с n неизвестными. Запишем систему (1) в матричной форме. Обозначим:
Тогда систему (1) можно записать в виде
Предположим,
что определитель
По формуле (3) находят решение системы методом обратной матрицы.
4. Метод Жордана-Гаусса для решения системы n линейных уравнений с n неизвестными. Алгоритм метода Жордана- Гаусса: 1 шаг. Рассмотрим одно из уравнений системы (1), назовем его разрешающим. 2 шаг. В этом уравнении выберем любое неизвестное с ≠ 0 коэффициентом (если есть возможность, то равным 1), назовем этот коэффициентразрешающим элементом. 3 шаг. Исключим выбранное неизвестное из всех уравнений, кроме разрешающего уравнения. 4 шаг. Повторяем шаги 1-3 для всех уравнений системы. Каждое уравнение должно быть разрешающим только один раз. После конечного числа шагов определяем решение системы или устанавливаем ее несовместность. Процесс решения проводится в таблицах. Переход от одной таблицы к другой осуществляется по правилам: 1. Разрешающая строка делится на разрешающий элемент. 2. Разрешающий столбец дополняется нулями. 3. Если в разрешающей строке (столбце) имеются нули, то соответствующие им столбцы (строки) переписываются без изменения. 4. Остальные элементы вычисляются по правилу «прямоугольника»:
Пример. Решить систему методом Жордана- Гаусса.
Решение.
Ответ: х1 = 1; х2 = 2; х3 = 3.
5. Теорема Кронекера-Капелли для исследования систем m линейных уравнений с n неизвестными.
Пусть дана система m линейных уравнений с n неизвестными:
Выпишем основную матрицу системы:
и
расширенную матрицу
Вопрос о разрешимости системы (4) в общем виде рассматривается в следующей теореме. Теорема Кронекера – Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы. rang A=rang B=r. (5) При этом, если r=n, то система имеет единственное решение. Если r<n, то система имеет бесконечное множество решений.
6. Базисные и свободные переменные. Пусть r<n. Любые r переменных системы (4) называются базисными (основными), если определитель матрицы коэффициентов при них, т.е. базисный минор, не равен нулю. Остальные n – r переменных называются свободными (неосновными). Решение системы уравнений (4) называется допустимым, если все хj ≥0, j = 1,…, n. Базисным решением системы (4) называется такое допустимое решение, в котором все n – r свободных переменных равны нулю.
|

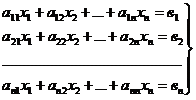 (1)
(1)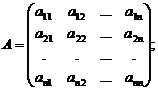




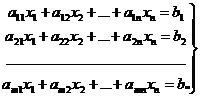 (4)
(4)
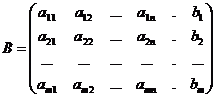 .
.