МатАн_ЛинАлг_080100 / Лекции_Математика_2_Дифференциальное исчисление

АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ «РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»

КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)

МАТЕМАТИКА, МАТЕМАТИЧЕСКИЙ АНАЛИЗ, ЛИНЕЙНАЯ АЛГЕБРА

ЛЕКЦИИ

Часть 2.

Функция. Дифференциальное исчисление

для студентов, обучающихся по специальности 036401.65 Таможенное дело

и направлениям подготовки

080100.62 Экономика, 080200.62 Менеджмент,

100100.62 Сервис, 100800.62 Товароведение

Казань 2012

Поташев А.В., Поташева Е.В. Математика, математический анализ, линейная алгебра. Лекции. Часть 2. Функция. Дифференциальное исчисление. – Казань: Казанский кооперативный институт, 2012. – 52 с.

Лекции разработаны в соответствии с учебными планами дисциплин «Математика», «Математический анализ», «Линейная алгебра», утвержденными ученым советом Российского университета кооперации от 22 марта 2011 г., протокол №4., и рабочими программами от 29.08.2011, протокол №1.

Рецензент: к.ф-м.н., доцент Николаева Н.В.

Одобрено и рекомендовано к изданию решением кафедры инженерно – технических дисциплин и сервиса от 9.09.2011, протокол № 2.

© Казанский кооперативный институт (филиал) Российского университета кооперации, 2012 © Поташев А.В., Поташева Е.В., 2012

2

РАЗДЕЛ. МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Тема 1. Предел функции

1.1.Введение в математический анализ

1.1.1.Множества, операции над ними

1.1.1.1.Основные понятия теории множеств

Теория множества была создана немецким математиком Г. Кантором (1845-1918) во второй половине XIX века. Понятие множества является одним из основных понятий математики.

Множество – это совокупность некоторых объектов, объединенных по какому-либо признаку в единое.

Например: множество студентов в аудитории, множество четных чисел, множество кривых на плоскости, множество корней уравнения и другие.

Объекты, из которых состоит множество, называются элементами множества.

Множества обозначаются большими буквами: A, B, X , Y , R, ...

Элементы множества обозначаются малыми буквами: a, b, x, y, r, ...

Если элемент a принадлежит множеству A, то пишут

			А
a A, если b не принадлежит A, то пишут b A (или b A ).			b
Множество A будем изображать в виде круга, а элементы			a
a и b – в виде точек (Рис. 1.1.1).			РИС. 1.1.1

Множества делятся на конечные и бесконечные. Конечные множества можно задать перечислением его элементов:

A = {a,b,c....d} .

Некоторые конечные и бесконечные множества можно задать характеристическим свойством его элементов – свойством, которым обладают все элементы этого множества и только они, записывается так:

A = {x : P(x)} ,

где знак «:» читается как «такое, что», «имеет место»,

3

P ( x) – характеристическое свойство.

Например,

	A = {x : x2 − 4 = 0} ,
		B = { x : x > 1} .
Множества	A и B называются равными, если они состоят из одинако-
вых элементов.
Обозначение: A = B .
Например,
	A = {x : x		2	− 9 =
					0}
	B =	{	−3, 3		A = B .
				}
Пустое множество – это множество, не содержащее ни одного элемента.
Обозначают пустое множество . Например,
	= {x : x2 + 1 < 0}
Множество	B называется подмножеством множества A, если любой

(каждый) элемент множества B принадлежит множеству A.

Обозначение: B A (иногда говорят: A включает B или B содержится в

A).

Примеры:

1) A – множество целых чисел, B – множество четных
чисел B A .		A
2) A – множество прямоугольников, B – множество	B
квадратов B A .
Геометрическая интерпретация B A (Рис. 1.1.2)	РИС. 1.1.2

1.1.1.2. Операции над множествами

1) Пересечение множеств

Пересечением множеств A и B называется множество, состоящее из элементов, принадлежащих A и B (Рис. 1.1.3).

Обозначение: A ∩B . Таким образом, A ∩B = {x : x A и x B} .

4

Множества A и B могут быть такими, что их пересечение будет пустым множеством: A ∩B = (Рис. 1.1.4).

		A		A
			B	B
		РИС. 1.1.3		РИС. 1.1.4
Примеры:
1) A = {1, 2,3, 4}, B = {3, 4,5,6}, A ∩ B = {3, 4}
2)	A –	множество прямоугольников
	B –	множество ромбов A ∩ B – множество квадратов.
3)	A –	множество рациональных чисел, B –		множество иррациональных

чисел. Тогда A ∩B = .

2) Объединение множеств.

Объединением множеств A и B называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств A или B (Рис. 1.1.5,

Рис. 1.1.6).

Обозначение: A B . Таким образом, A B = {x : x A или x B} .

а) б)

		A	B	A
				B
		РИС. 1.1.5		РИС. 1.1.6
Примеры:
1)	A = {1,2,3, 4}, B = {3, 4,5,6}, A B = {1, 2,3, 4,5,6 }
2)	A –	множество четных чисел
	B –	множество нечетных чисел		A B – множество целых чисел.

5

3) Разность множеств		а)	б)
Разностью множеств A и B называется		A	B	A	B
множество A B , состоящее из элементов	A,
не принадлежащих B (На Рис. 1.1.7 множе-			РИС. 1.1.7
ство A \ B выделено двойной штриховкой).

Примеры:

1) A = {1, 2,3, 4}, B = {3,4,5,6}, A\B = {1, 2} .

2) A – множество целых чисел, кратных 3. B – множество целых чисел, кратных 2.

A B – множество нечетных чисел, кратных 3.

Замечание:

Если A ∩ B = , то A B = A (Рис. 1.1.8).

А

В

РИС. 1.1.8

1.1.2.Числовые множества

1.1.2.1.Числовые множества

В математическом анализе будем иметь дело с множествами, элементами которых являются числа. Такие множества называются числовыми. Наиболее важные числовые множества:

= {1,2,3, 4....} – множество натуральных чисел;

= {...− 3, − 2, − 1,0,1, 2,3} – множество целых чисел;

	p
= x : x =		, p , q –	множество рациональных чисел;
	q

– множество действительных (вещественных) чисел.

При этом .

Каждое действительное число изображается точкой на координатной прямой (числовой оси) (Рис. 1.1.9).

6

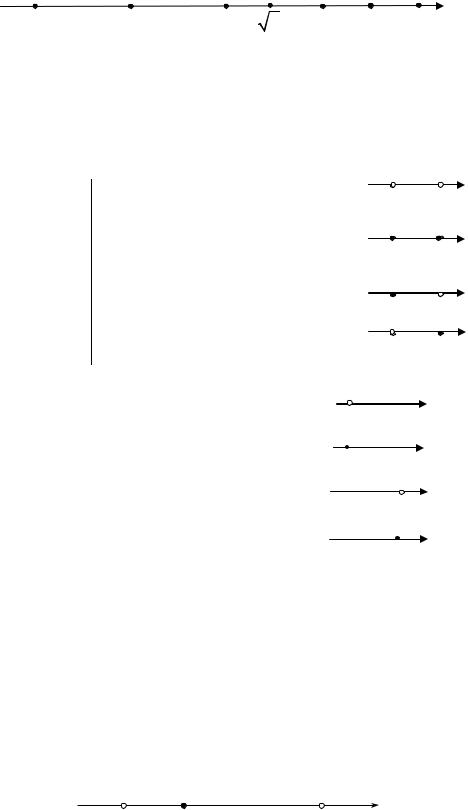
−1

0

1

2

2

2,5

3

x

РИС. 1.1.9

1.1.2.2. Интервалы

Рассмотрим подмножества множества (интервалы):

(a,b) = {x : a < x < b} [a,b] = {x : a £ x £ b}

[a,b) = {x : a £ x < b} (a,b] = {x : a < x £ b}

– открытый интервал

a

b x

– замкнутый интервал

a b x

(отрезок)

– полуоткрытые	a	b	x
интервалы	a	b	x

Неограниченные интервалы:
(a,¥) = {x : x > a}	a	x
[a,¥) = {x : x ³ a}	a	x
(-¥,b) = {x : x < b}	b	x
(-¥,b] = {x : x £ b}	b	x
= (-¥,¥) = {x : -¥ < x < ¥} –	вся числовая ось.

1.1.2.3. Окрестность точки

Введем понятие окрестность точки.

Окрестностью точки a называется любой открытый интервал, содержащий точку a (Рис. 1.1.10).

a

x

РИС. 1.1.10

Наибольший интерес представляет симметричный интервал с центром в точке a .

7

r-окрестностью точки a называется симметричный открытый интервал длины 2r с центром в точке a (Рис. 1.1.11). Величина r называется радиусом окрестности.

a − r

a

a + r x

РИС. 1.1.11

1.1.3.Элементы математической логики

1.1.3.1.Основные определения

Высказывание – это предложение, которое истинно или ложно.

Обозначение высказываний: A, B, C, ... X , Y , Z , ... Иногда для обозначе-

ния высказываний используются буквы с индексами: A1, A2 , B1, B2 ,...

Примеры:

1) A – « Волга впадает в Каспийское море» – истинно; 2) B – « 2 × 2=5» – ложно; 3) С – « Диагонали ромба перпендикулярны» – истинно.

Но не любое предложение является высказыванием. Например, предложения «Математика – важный предмет», «Который час?» не являются высказываниями, потому что не имеет смысла ставить вопрос, истинны они или ложны.

Предложение « x2 − 4 = 0 » становится высказыванием при конкретных значениях переменной x : если x = 2 или x = -2 получаем истинное высказывание, при остальных x – ложное.

Предложение, которое содержит переменные и становится высказыванием при подстановке вместо переменных их значений, называется предикатом.

Обозначение предикатов: A( x), B ( x, y ),....

1.1.3.2. Логические операции

Из высказываний с помощью союзов «и», «или», «если…., то», «тогда и только тогда, когда» и частицы «не» можно составлять более сложные высказывания. Союзы и частица «не» называются логическими связками. Высказывания, образованные из других высказываний с помощью логических связок,

8

называются составными. Высказывания, не являющиеся составными, называ-

ются элементарными.

Для каждого составного высказывания нужно определить истинно оно или ложно в зависимости от истинности или ложности высказываний, из которых оно построено. Чтобы не решать эту задачу для каждого конкретного случая, а решать ее в общем виде, введены логические операции: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.

Для каждого высказывания A введем число α ( A) , которое называется

значением истинности высказывания A.

Значением истинности высказывания A называется число α ( A) , опре-

деляемое равенством:

1,	если A − истинно,
α ( A) =	если A − ложно.
0,

Для составного высказывания составляется таблица истинности, указывающая значение его истинности в зависимости от значений истинности высказываний, из которых оно состоит.

Перейдем к описанию логических операций, для каждой из которых составим таблицу истинности.

1.1.3.3. Отрицание высказывания

Таблица ис-

Отрицанием высказывания A называется высказывание

тинности

A

, которое истинно, если A ложно, и ложно, если A истинно.

Логическая операция отрицание соответствует логической

A

A

связке «не».

1

0

0

1

1.1.3.4. Конъюнкция высказываний (логическое произведение)

Таблица истин-

Конъюнкцией высказываний A и B называется вы-

сказывание A B , которое истинно только в том случае, ко-

ности

гда истинны оба высказывания A и B .

A

B

A B

9

Иногда для обозначения конъюнкции будем применять				1		1		1
более краткую форму записи AB , то есть как обычное
				1		0		0
умножение.
				0		1		0
Конъюнкция A B соответствует логической связке
				0		0		0
«и».
1.1.3.5. Дизъюнкция высказываний (логическая сумма)
Дизъюнкцией высказываний A и B называется вы-				Таблица истин-
сказывание A B , которое ложно только в том случае, ко-						ности
гда ложны оба высказывания A и B .
				A		B		A B
Дизъюнкция A B соответствует логической связке
				1		1		1
«или».
				1		0		1
				0		1		1
				0		0		0
1.1.3.6. Импликация высказываний
Импликацией высказываний A и B называется вы-			Таблица истин-
сказывание A B , которое ложно только в том случае, ес-						ности
ли A – истинно, а B – ложно.
				A		B		A B
Импликация A B соответствует логической связке
			1			1		1
«если …, то … ».
			1			0		0
			0			1		1
			0			0		1

10