ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

ЛИНЕЙНЫЙ ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ, ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ, СВОЙСТВА, МЕТОДЫ НАХОЖДЕНИЯ

Задачи, приводящие к понятию определенного интеграла (линейного, двойного, тройного и криволинейного)

Задача. Найти массу пяти неоднородных тел различной формы с известными размерами:

1.прямолинейного тонкого стержня (обозначим его буквой L) длиной ℓ лин. ед.;

2.тонкого изогнутого стержня (обозначим его буквой L) длиной ℓ лин. ед.;

3.тонкой пластины D с площадью S кв.ед.;

4.тонкой изогнутой пластины q размером σ кв.ед.;

5.объемного тела W с объемом V куб.ед.

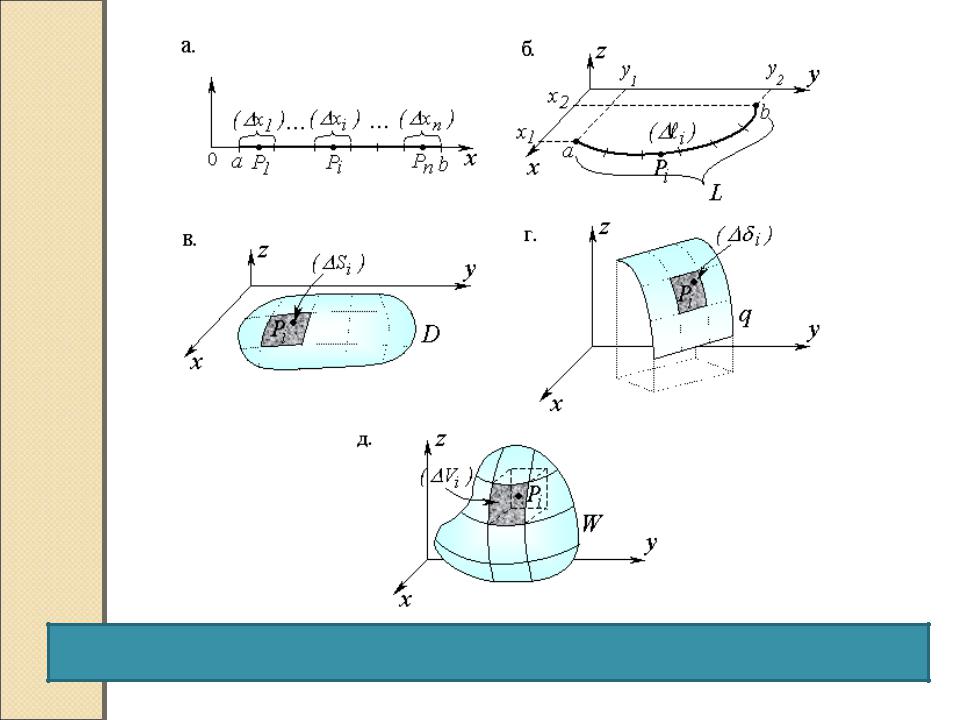
Неоднородные тела различной формы

МАССА ОДНОРОДНОГО ТЕЛА, ГДЕ ρ (Р) = const , РАВНА:

Произведение плотности тела на размер тела

Если бы тела были однородными, то их массу мы могли бы найти по формулам:

	M[a,b] (b a)	М[q]
		М[D] S
	М[L] l
		М[W ] V

В случае неоднородных тел поступим следующим образом:

1. Разобьем каждое тело на n малых частей произвольным образом:

№	Виды неоднородных тел	Обозначение элементов
		разбиения
1.	Прямолинейный тонкий	x1, x2 ,... xi ,... xn.
	стержень
2.	Тонкий изогнутый	l1, l2,... li ,... ln.
	стержень
3.	Тонкая плоская пластина	s1, s2,... si ,... sn.
4.	Тонкая изогнутая пластина	1, 2,... i ,... n.
5.	Объемное тело	1, 2,... i ,... n.

2.Внутри каждого частичного интервала разбиения неоднородных тел произвольным образом возьмем точки:

P1, P2,..., Pi ,..., Pn.

3.В выбранных точках найдем значение плотности массы неоднородных тел:

(P1), (P2 ),..., (Pi ),..., (Pn ).

4. Если плотность массы ρ (Р) – непрерывная функция и все тела разбиты на достаточно малые кусочки, то в пределах одной элементарной части всех тел ее приближенно можно считать постоянной, равной значению в выбранной точке ρ (Рi).

5. Тогда массу i-ой части каждого тела можно найти приближенно, как произведение плотности ρ(Рi) на размеры

№ Виды неоднородных тел Формула нахождения массы i-ой части неоднородного тела

1.	Прямолинейный тонкий	mi (Pi ) xi
	стержень
2.	Тонкий изогнутый стержень	mi (Pi ) l i
3.	Тонкая плоская пластина	mi (Pi ) Si
4.	Тонкая изогнутая пластина	mi (Pi ) i
5.	Объемное тело	mi (Pi ) Vi

6. Масса каждого из пяти неоднородных тел

будет равна сумме масс элементарных частей, на которые они были разбиты.

Заменяя элементарные массы их приближенными значениями, получим:

	№	Виды неоднородных тел	Формула нахождения
			массы неоднородных
			тел			n
			n
	1.	Прямолинейный тонкий	M[a,b] mi (Pi ) xi
			i 1			i 1
		стержень	n	n
	2.	Тонкий изогнутый стержень	M[L] mi (Pi ) l i
			i 1	i 1
			n	n
	3.	Тонкая плоская пластина	M[D] mi	(Pi ) Si
			i 1	i 1	n
	4.	Тонкая изогнутая пластина	n
			M[q] mi (Pi ) i
	5.	Объемное тело	i 1	i 1
			n			n
			M[q] mi (Pi ) i
			i 1			i 1

Определение. Диаметр элементарной части тела

– это максимальное из расстояний между двумя ее точками.

7. При n → ∞, или при стремлении к нулю наибольшего из диаметров элементарных кусочков, т.е. при переходе к пределу, мы получим точное значение для масс всех тел:

№	Виды неоднородных тел	Формула нахождения массы
		неоднородных тел
1.	Прямолинейный тонкий								n
		M[a,b]		lim					(Pi ) xi ,
	стержень
2.				max xi			0 i 1
	Тонкий изогнутый							n
	стержень	M[L]		lim			(Pi ) l i ,
3.			max l i 0 i 1
	Тонкая плоская пластина								n
		M[D]		lim		) 0			(Pi ) Si ,
4.	Тонкая изогнутая		max d ( S		i				i 1
									n
	пластина	M[q]		lim					(Pi ) i ,
		max d ( i ) 0 i 1
5.	Объемное тело	M[W ]							n	(P ) V .
				lim				) 0
			max d ( V							i i
							i		i 1

ВЫВОД ПО ЗАДАЧЕ:

Когда распределение значений различных физических величин неравномерное, решение довольно широкого класса задач сводится к одинаковым математическим операциям: к составлению суммы одного и того же вида и вычислению ее предела.