Приклади. Знайти модуль і аргумент комплексних чисел:

1.

2.

3.

Нехай Оскільки(рис. 1), то отримуємо

(2)

Цей запис називають тригонометричною формою комплексного числа. Інакше, поряд із зображенням (2) має місце і таке:

(3)

Звідси випливає: рівність двох комплексних чисел, заданих у тригонометричній формі, означає, що модулі цих чисел відрізняються на число, кратне .

Якщо та

Приклад. Записати в тригонометричній формі число

Маємо

Отже,

або в загальному вигляді тригонометрична форма числа

Додавати і віднімати комплексні числа, записані в тригонометричній формі, незручно. Однак операції множення і ділення над такими числами виконувати зручно. Нехай дано два числа:

.

Перемножимо ці числа

тобто

(4)

Співвідношення (4) є записом комплексного числа в тригонометричній формі,- модулем комплексного числа, а- аргументом цього числа.

Отже,

(5)

Таким чином, модуль добутку комплексних чисел дорівнює добутку співмножників, а аргумент добутку комплексних чисел дорівнює сумі аргументів співмножників.

Ці правила поширюються на будь-яке скінченне число множників

Припустимо, що і поділимона:

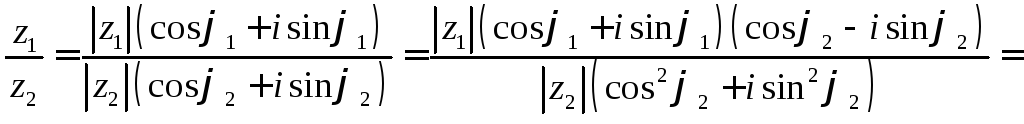
тобто

(6)

Звідси знаходимо

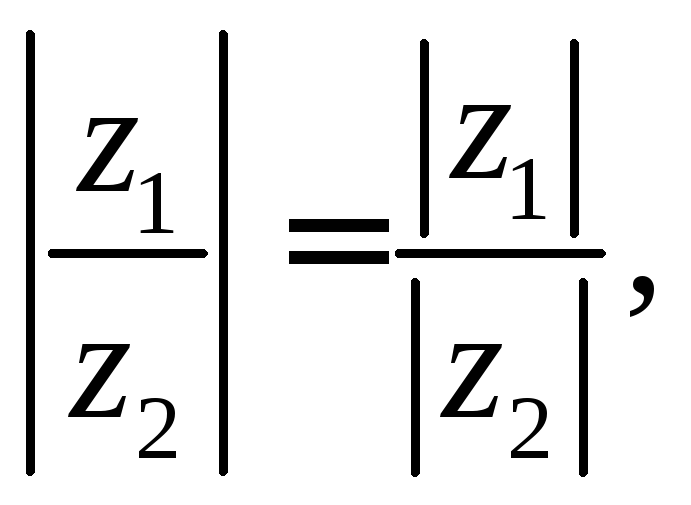
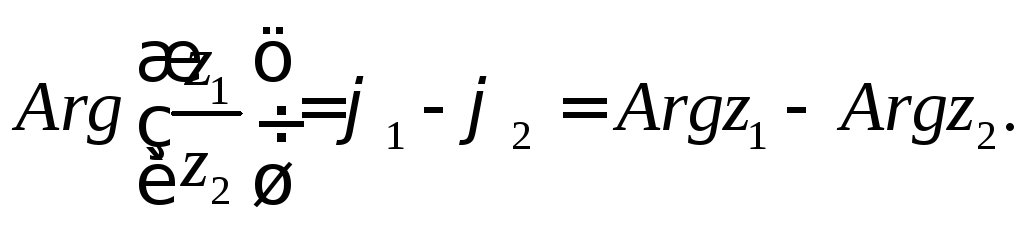
Отже, модуль частки двох комплексних чисел дорівнює модулю діленого, поділеному на модуль дільника; аргумент частки двох комплексних чисел дорівнює різниці аргуменів діленого і дільника.

Дамо геометричне тлумачення операцій над комплексними числами, зображаючи їх точками або напрямленими відрізками площини.

Н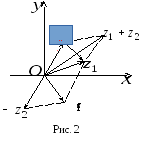ехай дано комплексні числаі. Зобразимо їх на площині векторами (рис 2). Тоді z₁+z₂ зображується діагоналлю паралелограма, побудованого на цих векторах, як на сторонах. Різниця z₁-z₂ дорівнює сумі z₁+(-z₂). Вектор, яким зображується число -z₂, симетричний вектору числа z₂ відносно початку координат.

Щоб побудувати вектор, який відповідає різниці досить сполучити кінець вектора числа z₂ з кінцем вектора числа z₁ і утворений вектор перенести паралельно самому собі, помістивши його початок у точку 0.

Таким чином, додавання і віднімання комплексних чисел в алгебраїчній формі з геометричної точки зору зводиться до додавання і віднімання векторів, якими зображуються ці числа.

Геометричний зміст множення і ділення комплексних чисел з‘ясувати також неважко, використавши запис їх у тригонометричній формі. Справді, нехай дано два комплексних числа

і

Для побудови вектора, що зображує добуток (рис. 3), треба повернути векторнавколо початку координат на куті потім подовжити його враз (прице буде не подовження а стиснення).

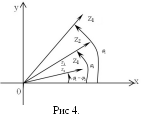
Для побудови вектора, що зображує частку (рис. 4), треба векторповернути навколо точки 0 на кут(тобто на кутза годинниковою стрілкою) і потім стиснути враз (прице буде не стиснення, а подовження).

Для модуля суми і модуля різниці справедливе таке твердження: Модуль суми двох комплексних чисел не більший від суми модулів цих чисел, а модуль різниці двох комплексних чисел не менший від абсолютної величини різниці модулів цих чисел.

Справді, розглянемо суму і різницю чисел z₁ і z₂

(рис. 5). На основі відомих співвідношень між сторонами трикутника маємо

, тобто

Рівності мають місце лише тоді, коли числа z₁ і z₂ зображуються векторами, що лежать на одній прямій.

3. Піднесення комплексного числа до цілого степеня.

Якщо комплексне число задане в алгебраїчній формі, тобто то для піднесення його до цілого додатного степеня треба застосувати формулу бінома Ньютона і тоді при будь-якому невід‘ємному ціломуузяти

Якщо комплексне число задане в тригонометричній формі, то піднесення його до цілого степеня виконують за формулою Муавра.

Теорема. Для будь-якого цілого числа справедлива рівність

(7)

яка називається формулою Муавра.

Спочатку методом математичної індукції доведемо справедливість формули (7) для натуральних . Приформула (7), очевидно, правильна.

Припустимо, що вона справедлива для , тобто

Доведемо, що вона справедлива і для , тобто

Дійсно,

Отже, формула (7) за принципом математичної індукції справедлива для будь-якого натурального показника .

Припустимо, що - ціле від‘ємне число. Вважатимемо, що(- натуральне число). Тоді

Отже, і при будь-якому цілому від‘ємному показнику формула (7) справедлива.

При справедливість формули (7) очевидна.

А. Муавр (1667-1754) – англійський математик (за походженням француз). Формулу названо ім‘ям Муавра тому, що в неявному вигляді вперше вона зустрічається в його працях, починаючи з 1707 р. Сучасного вигляду формулі Муавра надав Леонард Ейлер (1748 р.).

Приклади.

1.

2.

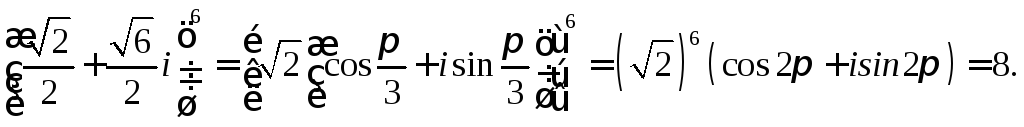
3.

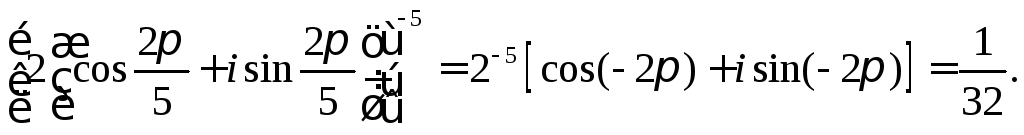
Якщо у формулі Муавра візьмемо то дістанемо рівність

(8)

Ця рівність дає змогу виразити ічерезі. Розклавши ліву частину рівності (8) за формулою бінома Ньютона, матимемо

(9)

Прирівнявши окремо дійсні частини й коефіцієнти уявних лівої і правої частин рівності (9), дістанемо записи ічерезі.

Покажемо це, наприклад, для .

звідки

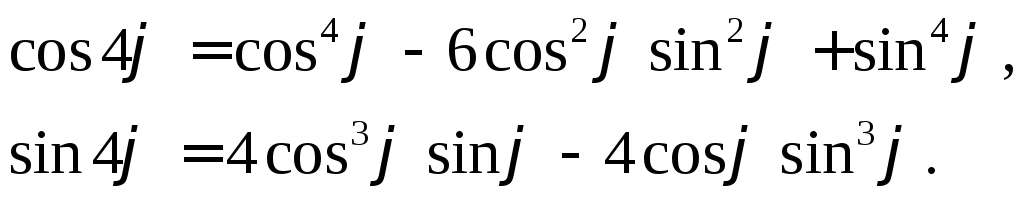
4. Добування кореня з комплексного числа

Розглянемо питання про добування квадратного кореня з комплексного числа. Припустимо, що квадратний корінь з числа існує і дорівнює, тобто

Тоді або

. (10)

Визначимо x і y. Для цього прирівняємо дійсні й уявні рівності (10). Дістанемо

(11)

(12)

Піднісши обидві частини кожної з цих рівностей до квадрата і почленно додавши їх, матимемо Звідси

(13)

(беремо додатне значення кореня, оскільки числа x і y дійсні, і, отже, ).

З рівностей (11) і (13) знаходимо

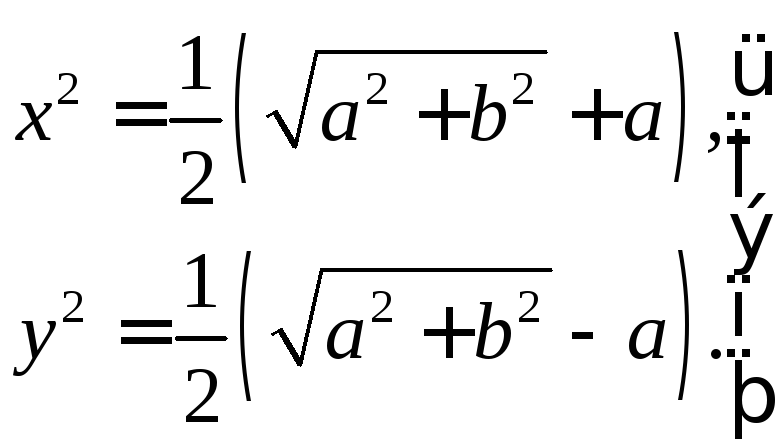(14)

Звідси випливає, що

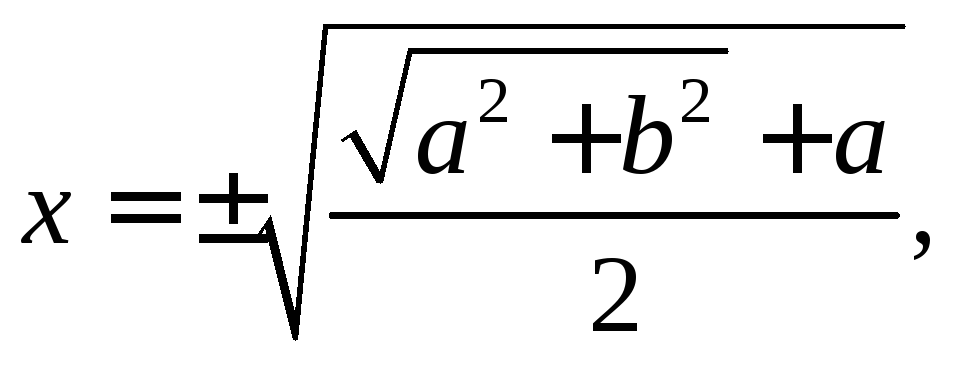
(15)

За рівність (12) знак добутку xy повинен збігатися із знаком числа b. Отже, при b>0 значення x і y повинні мати однакові знаки і тому радикали треба брати з Тим самим знаком. Якщо b<0, то значення x і y повинні мати протилежні знаки і, отже, радикали треба брати з тригонометричними знаками. Таким чином, маємо формули:

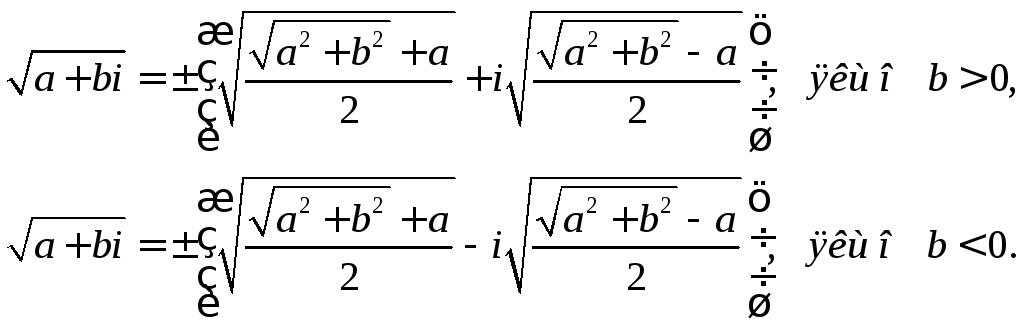(16)

Якщо то

Приклади. 1.

2. Розв‘язати рівняння

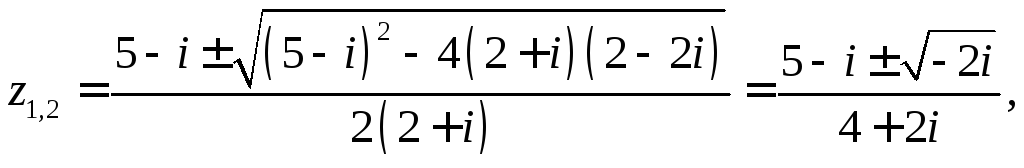
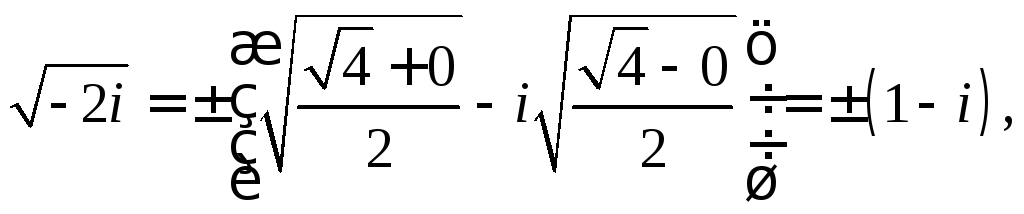
Добути корінь вищого (ніж другий) степеня з комплексного числа в алгебраїчній формі в загальному випадку неможливо.

Означення. Коренем n-го степеня (n-будь-яке натуральне число) з комплексного числа називатимемо таке число, що, і позначатимемо його символом

Нехай комплексне число задане в тригонометричній формі. Припустимо, що,. Тоді

.

Однак, за формулою Муавра,

.

Отже,

. (17)

Відомо, що два комплексні числа рівні тоді і тільки тоді, коли рівні їхні модулі, а аргументи або рівні, або відрізняютьбся доданком, кратним . Тому з рівності (17) випливає, що,де k- будь-яке ціле число. Звідси,де- арифметичне значення кореня з додатного числа, оскількиє число додатне.

Отже,

, (18).

- довільне ціле число.

Корінь n-го степеня з комплексного числа має лише n різних значень, які знайдемо за формулою (18) при Позначимо ці значення символамиТоді

(19)

Таким чином, має n значень, які визначаються за формулою (19).

З‘ясуємо, який геометричний зміст мають значення при. Всі n значеньмають той самий модуль. Аргументдорівнює, аргументидістаємо послідовним додаванням кута.

Отже, точки комплексної площини, якими зображують числа , є вершинами правильного n-кутника, вписаного в коло радіусаз центром у початку координат, причому одна з вершин зображує числоз аргументом, чим однозначно визначається положення всіх інших вершин.

Приклад. 1. Знайти .

Запишемо число в тригонометричній формі

Далі, за формулою (19), маємо

,

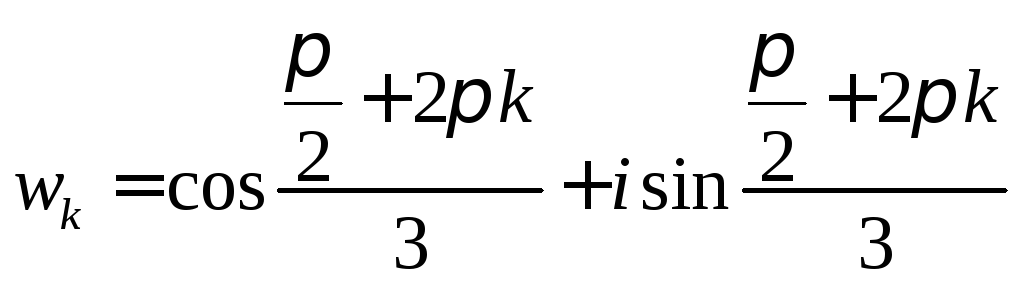Звідси дістанемо

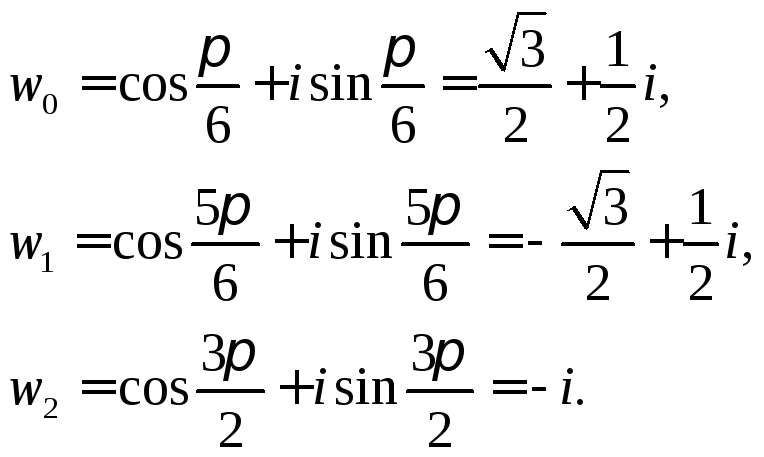
На рис. 6 зображено значення кореня 3-го степеня з числа .