kontrolnye / Обчислювальна математика / Лекции / r7

Раздел ¹ 7. Численное дифференцирование

Содержание

Выбор оптимального шага при численном дифференцировании	8
Исследование точности	9
Предметный указатель	10

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Численное дифференцирование применяется, если функцию y(x) трудно или невозможно продифференцировать аналитически — например, если она задана таблицей. Оно также необходимо при решении дифференцированных уравнений при помощи разностных методов.

При численном дифференцировании функцию y(x) аппроксимируют легко вычисляемой функцией φ(x; a) и приближенно полагают, что y0(x) = φ0(x; a). При этом можно использовать различные способы аппроксимации. Рассмотрим простейший способ — аппроксимацию интерполяционным многочленом Ньютона.

Пусть имеется функция f(x), которую необходимо продифференцировать несколько раз и найти эту производную в некоторой точке.

Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно его заменить более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных вообще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования.

Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции приближенно заменяется соответствующей производной интерполяционного многочлена

f(m)(x) ≈ L(nm)(x),

f(m)(x) ≈ ln(m)(x), 0 6 m 6 n.

Рассмотрим простейшие формулы численного дифференцирования, которые получаются указанным способом.

Будем предполагать, что функция задана в равностоящих узлах

xi = x0 + ih, h > 0, i = 0, ±1, ±2, . . . .

Ее значения и значения производных в узлах будем обозначать

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

называется первой разностной производной.

f(xi) = fi, f0(xi) = fi0, f00(xi) = fi00.

Пусть функция задана в двух точках x0 и x1 = x0 + h, ее значения f0, f1. Посстроим интерполяционный многочлен первой степени

l1(x) = f0 + (x − x0)f(x0; x1).

Производная l10 (x) равна

l10 (x) = f(x0; x1) = f1 − f0 . h

Производную функцию f(x) в точке x0 приближенно заменяем производной интерполяционного многочлена

f0	(x)	≈	f1 − f0	.	(7.1)
0			h

Величина f1 − f0 h

Пусть f(x) задана в трех точках x0, x1 = x0 + h, x−1 = x0 − h. Интерполяционный многочлен Ньютона второй степени имеет вид

l2(x) = f(x0) + (x − x0)f(x0; x1) + (x − x0)(x − x1)f(x0; x1; x−1).

Берем производную

l20 (x) = f(x0; x1) + (2x − x0 − x1)f(x0; x1; x−1).

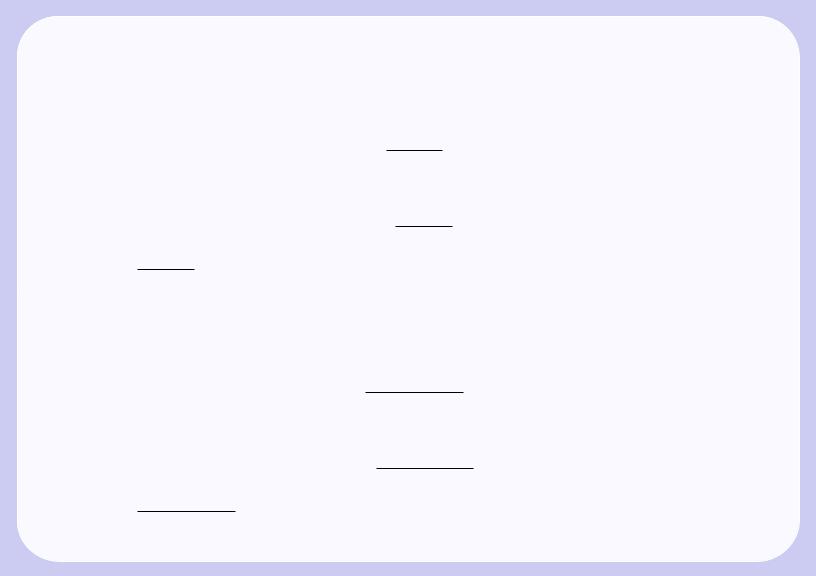
В точке x0 она равна

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

l20 (x0) = x1

− x0 + (x0 − x1) × (x0

x1)(x0

x−1)

+ (x1

x0)(x1

x−1) + (x−1

x0)(x−1

x1) =

f1

f0

f0

f1

f−1

−

−

−

−

−

−

−

=

f1 − f−1

.

2h

Получаем приближенную формулу

f0

≈

f1 − f−1

.

(7.2)

0

2h

Величина

f1 − f−1

называется центральной разностной производной.

2h

Наконец, если взять вторую производную

= 2

l20 (x) = 2f(x0; x1; x−1) =

f−1

=

f0

+

f1

+

(x0 − x1)(x0 − x−1)

(x1 − x0)(x1 − x−1)

(x−1 − x0)(x−1 − x1)

=

f1 − 2f0 + f−1

,

h2

получаем приближенную формулу.

f00

f1 − 2f0 + f−1

.

(7.3)

0 ≈

h2

Величина f1 − 2f0 + f−1 называется второй разностной производной. h2

Формулы (7.1)-(7.3) называются формулами численного дифференцирования.

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

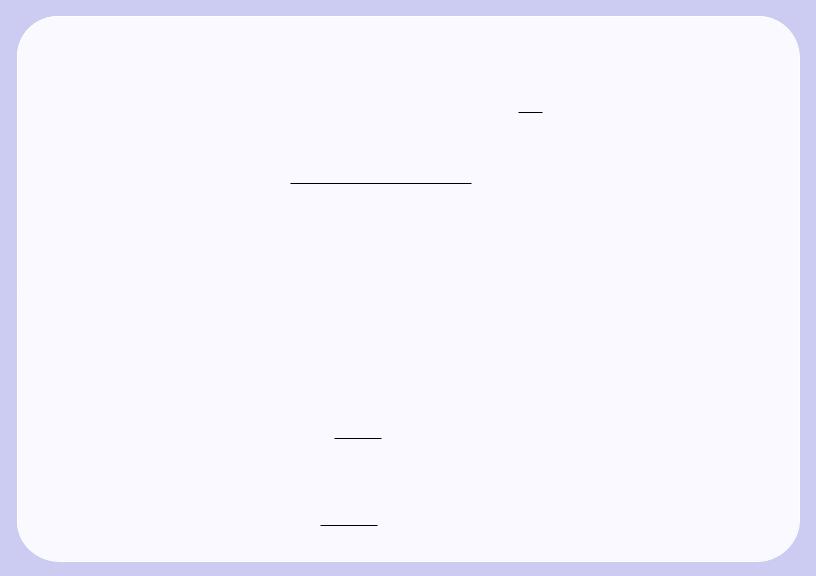
Предполагая функцию f достаточное число раз непрерывно дифференцируемой, получим погрешности приближенных формул (7.1)-(7.3).

В дальнейшем нам понадобится следующая лемма.

Лемма 1 Пусть f C [a, b], ξi [a, b] — произвольные точки, i = 1, n. Тогда существует такая точка

ξ [a, b], что

f(ξ1) + f(ξ2) + . . . + f(ξn) = f(ξ). n

Доказательство. Очевидно неравенство

	min f(x) 6	f(ξ1) + f(ξ2) + . . . + f(ξn)		6 max f(x).
		n
	[a,b]			[a,b]

По теореме Больцано-Коши о промежуточных значениях непрерывной функции на замкнутом от-

резке она принимает все значения между min f(x) и max f(x). Значит существует такая точка ξ [a, b],

[a,b] [a,b]

что выполняет указанное в лемме равенство.

Погрешности формул численного дифференцирования дает следующая лемма.

Лемма 2 1. Предположим, что f C2 [x0, x1]. Тогда существует такая точка ξ, что

f0

=

f1 − f0

−

h

f00(ξ),

x

< ξ < x

.

(7.4)

h

2

0

0

1

2. Если f C3 [x−1, x1] , то существует такая точка ξ, что

f0

=

f1 − f−1

−

h2

f000(ξ),

x

< ξ < x

.

(7.5)

−1

0

2h

6

1

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

3. Когда f C4 [x−1, x1], то существует ξ такая, что

f

00 =

f−1 − 2f0 + f1

−

h2

f(4)

(ξ),

x

< ξ < x

.

−1

0

h2

12

1

Доказательство. По формуле Тейлора

f1 = f0 + hf00 +

h2

f00 (ξ) , ξ (x0, x1) ,

2

откуда следует (7.4).

Если f C4 [x−1, x1], то по формуле Тейлора

h2

h3

h4

f±1 = f0 ± hf00 +

f000 ±

f0000 +

f(4) (ξ±) ,

2

6

24

где x−1 < ξ− < ξ+ < x1.

Подставим (7.7) в

f−1 − 2f0 + f1

. Получаем

h2

f

2f

+ f

h2

f(4) (ξ−) + f(4) (ξ+) .

−1

− 0

1

= f000 +

h2

24

Заменяя в соответствии с леммой 1

f(4) (ξ−) + f(4) (ξ+) = 2f(4) (ξ) ,

x−1 < ξ < x1,

получаем

(7.6)

(7.7)

f−1 − 2f0 + f1	= f00	+	h2	f(4) (ξ) .
h2	0	12

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Откуда и следует (7.6).

Равенство (7.5) доказывается аналогично (доказательство провести самостоятельно).

Формулы (7.4)-(7.6) называются формулами численного дифференцирования с остаточными членами.

Погрешности формул (7.1)-(7.3) оцениваются с помощью следующих неравенств, которые вытекают из соотношений (7.4)-(7.6):

f0

f1

− f0

h

max

f00

(x) ,

1

0 −

h

6 2 [x0,x1] |

|

f0

− −

6

max

f000 (x) ,

0

f

h2

[x

1,x1]

−

2h

6

−

|

|

f

1

2f0 + f1

h2

f00

−

−

max

f(4) (x) .

2

6

0

−

h

[x

−

1,x1]

12

Говорят, что погрешность формулы (7.1) имеет первый порядок относительно h (или порядка h), а погрешность формул (7.2) и (7.3) имеет второй порядок относительно h (или порядка h2). Также говорят, что формула численного дифференцирования (1) первого порядка точности (относительно h), а формулы (7.2) и (7.3) имеют второй порядок точности.

Указанным способом можно получать формулы численного дифференцирования для старших производных и для большего количества узлов интерполирования.

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Выбор оптимального шага при численном дифференцировании

Допустим, что граница абсолютной погрешности при вычислении функции f в каждой точке удовлетворяет неравенству

fi 6 .			(7.8)

Пусть в некоторой окрестности точки x0 производные, через которые выражаются остаточные члены в формулах (7.5), (7.6), непрерывны и удовлетворяют неравенствам

|f000 (x)| 6	M	3,	f(4)	(x)	6	M	4,	(7.9)

где M3, M4 — некоторые числа. Тогда полная погрешность формул (7.2), (7.3) (без учета погрешностей округления) в соответствии с (7.5), (7.6), (7.8), (7.9) не превосходит соответственно величин

+

h2

ε1

=

+

M3

,

2h

6

h2

+ 2Δ +

ε2

=

+

M4.

h2

12

Минимизация по h этих величин приводит к следующим значениям h:

h1 =			M3			1	,	h2	= 2	M4							1		(7.10)
				3Δ		3						3Δ					4
при этом
				3 −2			1											1
	3		M				3						M4				2
ε1 =							,	ε2 = 2										.	(7.11)
	2		3											3

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Если при выбранном для какой-либо из формул (7.2), (7.3) значении h отрезок [x−1, x1] не выходит за пределы окрестности точки x0, в которой выполняется соответствующее неравенство (7.9), то найденное h есть оптимальным и полная погрешность численного дифференцирования оценивается соответствующей величиной (7.11).

Исследование точности

Исследование точности полученных выражений при численных расчетах удобно делать при помощи апостериорной оценки, по скорости убывания членов соответствующего ряда Тейлора. Если шаг сетки достаточно мал, то погрешность близка к первому отброшенному члену.

Таким образом порядок точности результата по отношению к шагу сетку равен числу оставленных в ней членов, или другими словами, он равен числу узлов интерполяции минус порядок производной. Поэтому минимальное число узлов необходимое для вычисления m-ой производной, равно m + 1; оно обеспечивает первый порядок точности.

Эти выводы соответствуют принципу: при почленном дифференцировании ряда скорость его сходимости уменьшается.

Если учесть ухудшение сходимости ряда при дифференцировании, то можно сделать вывод: даже если функция задана хорошо составленной таблицей на довольно подробной сетке, то практически численным дифференцированием можно определить первую и вторую производные, а третью и четвертую — лишь удовлетворительно. Более высокие производные редко удается вычислить с удовлетворительной точностью.

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Предметный указатель

разностная производная вторая, 4 первая, 3 центральная, 4

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель