термех

1

Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил. Первый закон (закон инерции): изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы, а именно: произведение массы материальной точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы. Третий закон (закон равенства действия и противодействия) две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны. Задачи динамики. Для свободной материальной точки задачами динамики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики); 2) зная действующие на точку силы, определить закон движения точки (вторая, или основная, задача динамики).

2

Уравнения в декартовых координатах. Из кинематики известно, что движение точки в прямоугольных декартовых координатах задается уравнениями Уравнения в проекциях на оси естественного трехгранника.

3

Уравнение называют дифференциальным уравнением прямолинейного движения точки. Если для данной конкретной задачи дифференциальное уравнение будет проинтегрировано, то в полученное решение войдут две постоянные интегрирования С1 и С2 и общее решение уравнения будет иметь вид . Так как Q=const, то умножив обе части уравнения на dt и беря от них интегралы, найдем, что. Замена в этом равенстве vx на dx/dt дает . Проделаем операцию еще раз .

.

4

, , , все уравнения и теоремы механики для относительного движения точки составляются так же, как уравнения абсолютного движения, если при этом к действующим на точку силам взаимодействия с другими телами прибавить переносную и кориолисову силы инерции.

5

6

.диф-ное ур-ние движниия разделим оби части на m и полечим Уравнение представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. если то . Тогда ,такие колебания назыв гармоническими. ,. По начальным условиям , тогда .

7

,Тогда , и дифференциальное уравнение движения будет деля m получаем , где .

8

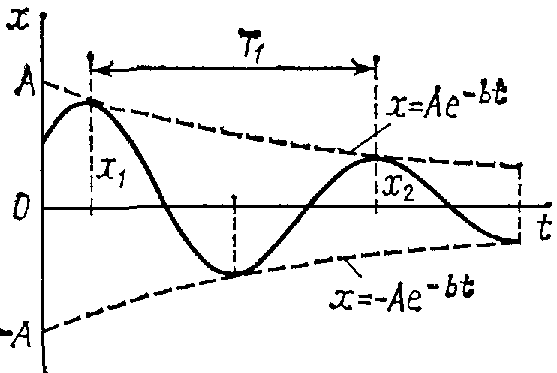
Эта сила называется возмущающей силой, а колебания, происходящие при действии такой силы, называются вынужденными. , где р-частота этой силы. - возмущающая сила(гармонической). 1. Вынужденные колебания при отсутствии сопротивления. . и диф ур-ние движения ,

2. Вынужденные колебания при вязком сопротивлении.

9

Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси: .осевой момент инерции является мерой инертности тела при вращательном движении. Для одной материальной точки . Для множества точек Радиусом инерции тела относительно оси Оz называется линейная величина , определяемая равенством

10

Формула выражает следующую теорему Гюйгенса: момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.

11

,где то , а если через центр масс то

12

КОЛЬЦО

ДИСК ТОГДА

13

Уравнение ) и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.

14

Количеством движения() материальной точки называется векторная величина то, равная произведению массы точки на ее скорость[.]

Количеством движения системы будем называть векторную величину Q, равную геометрической сумме (главному вектору) количеств движения всех точек системы, количество движения системы равно произведению массы всей системы на скорость ее центра масс.

15

Элементарным импульсом силы называется векторная величина dS, равная произведению силы F на элементарный промежуток времени dt: . Следовательно, импульс силы за некоторый промежуток времени равен определенному интегралу от элементарного импульса взятому в пределах от нуля до .

16

Уравнение выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил. Уравнение выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени.

17

Уравнение выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил. как интегралы, стоящие справа, дают импульсы внешних сил.

Уравнение выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени.

если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению. при этом

20

теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра.

равенство выражает теорему моментов относительно оси.

19

Главным моментом количеств движения (или кинетическим моментом) системы относительно данного центра О называется величина Ко, равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра *: . относительно координатных осей: . кинетический момент вращающегося тела относительно оси вращения равен произведению момента -инерции тела относительно этой оси на угловую скорость тела. . главный момент количеств движения (кинетический момент) системы может рассматриваться как характеристика ее вращательного движения.

18

моментом количества движения точки относительно некоторого центра О называется векторная величина , определяемая равенством относительно оси: ,

21

уравнение выражает следующую теорему моментов для системы: производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра. если сумма моментов относительно данного центра всех приложенных к системе внешних сил равна нулю, то главный момент количеств движения системы относительно этого центра будет численно и по направлению постоянен.

22

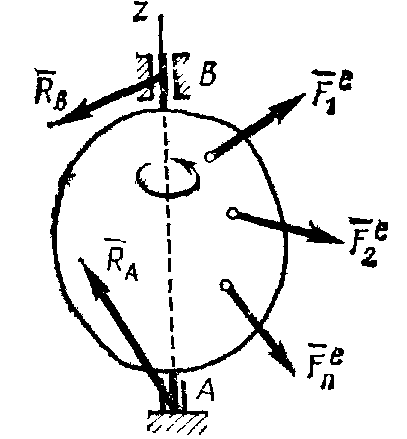Будем в дальнейшем величину Mz называть вращающим моментом. . Уравнение представляет собой дифференциальное уравнение вращательного движения твердого тела. Из него следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающемуся моменту:

23

Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости.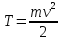

Кинетической энергией системы называется скалярная величина Т, равная сумме кинетических энергий всех точек системы:

или . кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

24

Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс.

25

Элементарной работой силы F, приложенной в точке М , называется скалярная величина , или

26

или , Следовательно, работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения.

27

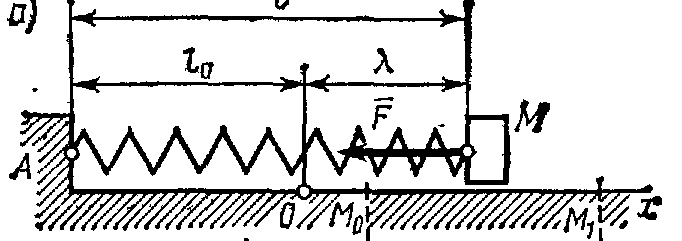
работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины. Работа будет положительной, когда т. е. когда конец пружины перемещается к равновесному положению, и отрицательной, когда т. е. когда конец пружины удаляется от равновесного положения. Можно доказать, что работа силы упругости остается справедливой и вслучае, когда перемещение точки М не является прямолинейным. Таким образом, оказывается, что работа силы F зависит только от значений и не зависит от вида траектории точки М. Следовательно, сила упругости также является потенциальной.

29

Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости.

Вырожаем:

выражение теоремы об изменении кинетической энергии точки в дифференциальной форме:

Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках найдем окончательно теорема об изменении кинетической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

30

Для каждой точки системы

Составляя такие уравнения для каждой из точек системы и складывая их почленно, и получим вырожение в диффирицеальной форме

или .

Проинтегрировав обе части получим Это уравнение выражает теорему об изменении кинетической энергии в другой (интегральной) форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.

31

Область, в каждой точке которой на помещенную туда материальную частицу действует сила, зависящая от положения (координат) этой точки, называется силовым полем. Так как сила определяется ее проекциями на координатные оси, то силовое поле задается уравнениями:

тогда элиментарная работа равна . Функция U от координат х, у, z, дифференциал которой равен элементарной работе, называется силовой функцией. Силовое поле, для которого существует силовая функция, называется потенциальным силовым полем, а силы, действующие в этом поле,—потенциальными силами.

32

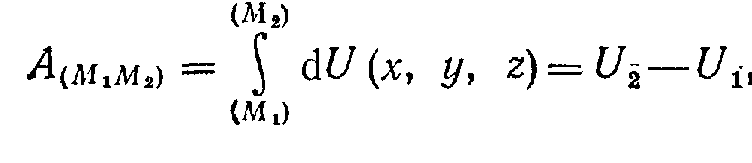Следовательно, работа потенциальной силы равна разности значений силовой функции в конечной и начальной точках пути и от вида траектории движущейся точки не зависит. Силы, работа которых зависит от вида траектории или от закона движения точки приложения силы, называются непотенциальными.

Потенциальной энергией материальной точки в данном положении М называется скалярная величина П, равная той работе, которую произведут силы поля при перемещении точки из положения М в нулевое . Будем в дальнейшем считать нулевые точки для функций П (х, у, г) и U (х, у, z) совпадающими. Тогда Uo=0 и , где U — значение силовой функции в точке М поля. Таким образом, , т. е. потенциальная энергия в любой точке силового поля равна значению силовой функции в этой точке, взятому с обратным знаком. , Следовательно, работа потенциальной силы равна разности значений потенциальной энергии движущейся точки в начальном и конечном ее положениях.

Закон сохранения механической энергии.

Физическим маятником называется твердое тело, которое может совершать колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. воспользуемся дифференциальным уравнением вращательного движения

Деля обе части равенства на и вводя обозначение

дифференциальное уравнение колебаний маятника . Полученное дифференциальное уравнение в обычных функциях не интегрируется. Ограничимся рассмотрением малых колебаний маятника, считая угол малым и полагая приближенно , Это дифференциальное уравнение совпадает по виду с дифференциальным уравнением свободных прямолинейных колебаний точки Тогда закон малых колебаний маятника при данных начальных условиях будет

33

Один из экспериментальных методов определения моментов инерции тел (метод маятниковых колебаний) основан на использовании формулы периода малых колебаний маятника. . После этого искомый момент инерции вычисляется по теореме Гюйгенса: .

34

уравнения движения точки С найдем по теореме о движении центра масс

а вращательное движение вокруг центра С будет определяться уравнением , тогда получим дифференциальные уравнения плоскопараллельного движения твердого тела.

35

Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки. Тогда оказывается, что движение точки обладает следующим свойством: если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной, т. е. .Это положение выражает принцип Даламбера для материальной точки.

36

принцип Даламбера для системы: если в любой момент времени к каждой из точек системы кроме действующих на нее внешних и внутреннихсил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики. введем обозначение, . Величины представляют собою главный вектор и главный

момент относительно центра О системы сил инерции.

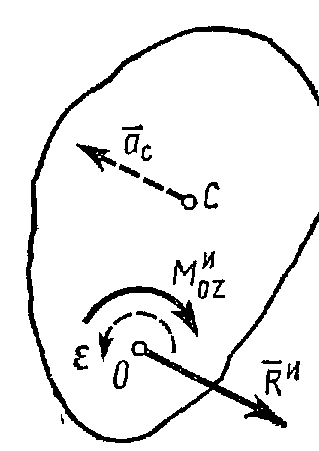
Приведение сил инерции твердого тела. Согласно результатам § 12, справедливым для любых сил, систему сил инерции твердого тела можно заменить одной силой, равной и приложенной в произвольно выбранном центре О, и парой с моментом, равным -

37

, главный вектор сил инерции механической системы (в частности, твердого тела) равен произведению массы системы (тела) на ускорение центра масс и направлен противоположно этому ускорению.

главный момент сил инерции механической системы (твердого тела) относительно некоторого центра О или оси z равен взятой со знаком минус производной по времени от кинетического момента системы (тела) относительно того же центра или той же оси.

38

,

Вращение вокруг оси, проходящей через центр масс тела. Если тело, рассмотренное в п. 2, вращается вокруг оси Cz, проходящей через центр масс С тела, то , так как . Следовательно, в этом случае система сил инерции тела приводится к одной только паре с моментом , лежащей в плоскости симметрии тела.