Лекция № 2 Аксиоматика теории вероятностей. Правила сложения и умножения вероятностей и их следствия. Модели надежнлсти технических систем. Сумма и произведение событий.

Пусть производится некоторый опыт (эксперимент, испытание) со случайным исходом. Рассмотрим множество Ω всех возможных исходов опыта; каждый его элемент ωΩ будем называть элементарным событием, а все множество Ω – пространством элементарных событий. Любое событие А в теоретико-множественной трактовке есть некоторое подмножество Ω: А  Ω.

Среди событий, являющихся подмножествами множества Ω, можно рассмотреть и само Ω (ведь каждое множество есть свое собственное подмножество); оно называется достоверным событием. Ко всему пространству Ω элементарных событий добавляется еще и пустое множество ; это множество тоже рассматривается как событие и называется невозможным событием.

Заметим, что элементарные события ω в одном и том же опыте можно задавать по-разному; например, при случайном бросании точки на плоскость положение точки можно задавать как парой декартовых координат (х,у), так и парой полярных (,).

Суммой двух событий А и В называется событие С, состоящее в выполнении события А или события В, или обоих событий вместе.

Пример.

Опыт: выбор карты из колоды.

События: А – появление трефовой масти, В – появление туза, С – появление трефовой масти (А) или туза (В)

С=А+В

Геометрическая интерпретация.

Пусть множество всех точек плоскости представляет собой пространство элементарных событий Ω.

Опыт – выбор произвольной точки.

Событие А – появление точки в области А

Событие В – появление точки в области В

Событие С – появление точки в заштрихованной области

С = А + В ( С = А U В )

Суммой нескольких событий называется событие, состоящее в выполнении хотя бы одного из событий.

Произведением двух событий А и В называется событие D, состоящее в совместном выполнении события А и события В.

Пример.

Опыт: выбор карты из колоды.

События: А – появление трефовой масти, В – появление туза, D – появление трефового туза.

D = А · В ( D = А ∩ В )

Геометрическая интерпретация.

Пусть множество всех точек плоскости представляет собой пространство элементарных событий Ω.

Опыт – выбор произвольной точки.

D= А · В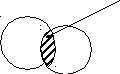

( D= А ∩ В )

А

А

С

В

В

обытие А – появление точки в области А

Событие В – появление точки в области В

Событие D – появление точки и в области А и в области В.

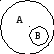А + В = А

А · В = В

Произведением нескольких событий называется событие, состоящее в совместном выполнении всех этих событий.

Дадим теоретико-множественное истолкование тем свойствам событий, которые мы рассматривали в первой лекции.

Несколько событий А₁, А₂, ..., А_n образуют полную группу, если Аi = Ω, т.е. их сумма (объединение) есть достоверное событие.

Два события А, В называют несовместными, если соответствующие множества не пересекаются, т.е. АВ = .

Несколько событий А₁, А₂, ..., А_n называются попарно несовместными (или просто несовместными), если появление любого из них исключает появление каждого из остальных: A_iA_j =  (при i j).

Определение вероятности. Правило суммы.

На основе вышеизложенной трактовки событий как множеств сформулируем аксиомы теории вероятностей. Пусть каждому событию А ставится в соответствие некоторое число, называемое вероятностью события. Вероятность события А будем обозначать Р(А). Так как любое событие есть множество, то вероятность события есть функция множества.

Потребуем, чтобы вероятности событий удовлетворяли следующим аксиомам:

1. Вероятность любого события заключена между нулем и единицей:

0  Р(А)  1

2. Если А и В несовместные события (АВ=Æ), то

Р(А+В) = Р(А) + Р(В)

Эта аксиома легко обобщается ( с помощью сочетательного свойства сложения ) на любое число событий: если А_iА_j = Æ при i  j, то

,

т. е. вероятность суммы несовместных событий равна сумме их вероятностей.

Аксиому сложения вероятностей иногда называют «теоремой сложения» (для опытов, сводящихся к схеме случаев, она может быть доказана), а также правилом сложения вероятностей.

3. Если имеется счетное множество несовместных событий A₁, A₂, ..., A_n, ... (A_iA_j = Æ при i  j), то

Третью аксиому приходится вводить отдельно, так как она не выводится из второй.

Правило сложения вероятностей имеет ряд важных следствий. В качестве одного из них докажем, что сумма вероятностей полной группы несовместимых событий равна единице, т.е. если

то

• P(A_i) = 1.

Действительно, так как события A₁, A₂, ..., A_n несовместны, то к ним применимо правило сложения:

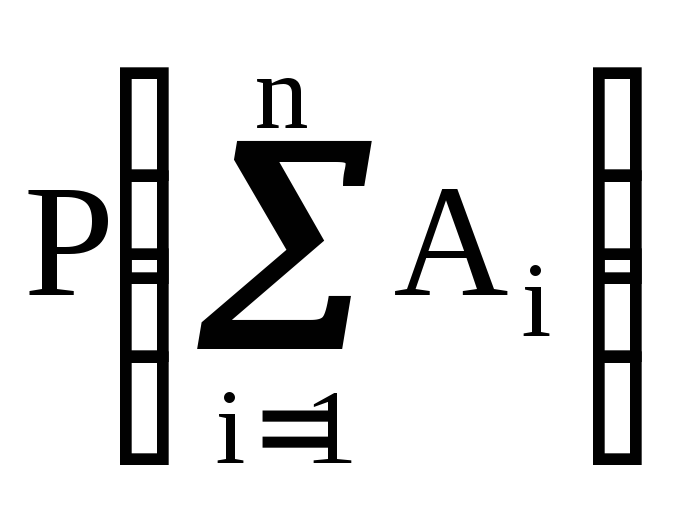
= ∑ P(A_i ) = P(Ω) = 1.