3. Классическое определение вероятности события. Теорема умножения и её свойства.

Вероятностью события А называется отношение числа событий благоприятствующих событию А к общему числу единственновозмож-ных, равновозможных и несовместных событий. Обозначается Р(А). 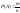, гдеm - число событий благоприятствующих событию А, n – общее число единственновозможных, равновозможных и несовместных событий.

Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е. P(AB)=P(A)*P_А(B), Р(АВ)=Р(В)*Р_В(А).

Док-во. Пусть из n единственновозможных, равновозмож-ных и несовместных событий, m событий, благоприятствующих соб.А, l – событие благоприятствует событию В, k – их совместному наступлению, т.е. А*В. Воспользуемся классическим определением вероятности события:

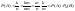
Аналогично можно доказать справедливость второй формулы.

Следствия:

1.Если вероятность событий отличны от 0, то P_А(B)=P(AB)/P(A), P_B(A)=P(AB)/P(B).

2.Если А независит от В, то В независит от А, т.е. они взаимонезависимы. P_B(A)=P(A);

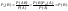
3.Из независимости событий А и В следует независимость пар событий: А и

1.Вероятность произведения двух независимых событий равна произведению их событий:

Р(АВ)=Р(А)*Р(В)

10. Теорема суммы и следствия из нее. Теорема.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Р(А+В)=Р(А)+Р(В)-Р(АВ)

Док-во. Пусть из n единственновоз-можных, равновозможных и несовместных событий, m событий благоприятствует событию А, l – соб.B, k – их совместному наступлению. По определению суммы двух событий А+В – либо А, либо В, либо А*В. Соб. А благоприятствует m-k событий, соб.В

l-k событий, а соб. АВ k событий. Таким образом, соб. А+В благоприятствует m-k+l-k+k=m+l-k событий. Воспользуемся классическим определением вероятности событий:

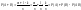Следствия:

1.Вероятность суммы двух несовместных событии равна сумме их вероятностей. P(A+B)=P(A)+P(B).

2.Сумма вероятностей событий, которые образуют полную группу =1 P(A₁)+P(A₂)+…+P(An)=1

3.Для взаимно противоположных событий А и Ā: Р(А)+Р(Ā)=1

4.Вероятность появления хотя бы одного из событий А₁, А₂, …, А_n равна: P(A₁+A₂+…+An)=1–P(Ā₁+Ā₂+…+Ān).

8. Дисперсия дсв и ее св-ва. 3 на выбор доказать.

Дисперсией дискретной СВ называется матем. ожидание квадрата её отклонения от матем. ожидания. D(X)=M[X-M(X)]². Из определения матем. ожидания дискретной СВ следует, что:

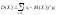
На практике при вычеслении дискретной СВ удобно пользоваться формулой: D(X)=M(X²)-M²(X).

Свойства D(X):

1. Дисперсия постоянной величины равна 0: D(C)=0

Док-во. D(C)=M(C²)-[M(С)]² = C²-C²=0

2. Постоянный множитель можно вынести за знак дисперсии возводя его в квадрат: D(kX)=k²D(X)

Док-во. D(kX)=M(k²X²)-[M(kX)]²=k²M(X²)-[kM(X)]²= =k²M(X²)-k²[M(X)]²=k²[M(X²)-M²(X)]=k²D(X)

3. Дисперсия алгебраической суммы (разницы) конечного числа независимых дискретных СВ равна сумме их дисперсий. D(X±Y)=D(X)+D(Y).

Док-во.1) Рассмотрим D(X+Y)=D(X)+D(Y),

По формуле вычисления дисперсии имеем:

D(X+Y)= M[(X+Y)²]-M²(X+Y), раскрыв скобки и пользуясь свойствами матем. ожидания суммы нескольких величин и произведения 2 CВ получим:

D(X+Y)=M(X²+2XY+Y²)-[M(X)+M(Y)]²= =M(X²)+2M(X)M(Y)+M(Y²)-M²(X)-2M(X)M(Y)-M²(Y)= =[M(X²)-M²(X)]+[M(Y²)-M²(Y)]=D(X)+D(Y)

2) Рассмотрим D(X-Y)=D(X)+D(Y),

D(X-Y)=D(X+(-1)Y), следуя предыдущему случаю имеем:

D(X-Y)=D(X+(-1)Y)=D(X)+D(-Y)=D(X)+D((-1)Y)=

=D(X)+(-1)²D(Y)=D(X)+D(Y)

4. Дисперсия любой CВ неотрицательна