CKT_l.r.02_NU / Решение нелинейных уравнений в Mathcad

6

1. Розв’язання нелінійних рівнянь

Часто на практиці при моделюванні різних процесів (технічних, економічних, фізичних, соціальних тощо) зустрічаються задачі, розв’язання яких зводиться до чисельного розв’язання нелінійних рівнянь або систем нелінійних рівнянь.

Нижче наведено теоретичну довідку з питань чисельних методів розв’язання нелінійних рівнянь або систем нелінійних рівнянь, можливості сис- теми комп’ютерної математики Mathcad при розв’язанні такого роду задач, а також контрольні завдання до розділу.

1.1.Розв’язання нелінійних рівнянь з одним невідомим

Вінженерних, наукових та економічних розрахунках доволі часто виникає необхідність розв’язання рівнянь, що мають вигляд:

f (x) = 0 ,

(1)

де функція f(x) визначена і неперервна на деякому скінченому або нескінченному інтервалі a ≤ x ≤ b .

Рівняння (1) називається лінійним відносно x , якщо функція f(x) має ви-

гляд a1x + a 0 . Для всіх інших випадків рівняння (1) – нелінійне.

Якщо f(x) являє собою алгебраїчний многочлен, то рівняння (1) називається алгебраїчним. Якщо ж у функцію входять елементарні функції (тригонометричні, логарифмічні, показникові тощо), то таке рівняння називається трансцендентним.

Значення x* , що перетворює рівняння (1) у тотожність, тобто f (x* ) ≡ 0 ,

називається коренем рівняння (1).

Точно знайти корені рівняння (1) вдається лише в окремих випадках. Тому розроблено чисельні методи розв’язання рівняння (1), які дозволяють обчислити наближені значення кореня цього рівняння з заданою точністю.

Процес обчислення коренів нелінійного рівняння складається з двох етапів:

1)відокремлення коренів, тобто визначення доволі малих відрізків – відрізків локалізації (ізолювання), в яких знаходиться лише один корінь рівняння; а також має виконуватися умова: f (a) × f (b) < 0 ;

2)уточнення кореня, тобто доведення його значення до заданої точності.

Реалізацію 1-го етапу (етапу відокремлення коренів) можна здійснити за допомогою графічних можливостей Mathcad, тобто візуально підібрати на графіку функції y = f (x) границі відрізків локалізації коренів цього рівняння. Це суттєво спрощує розв’язання поставленої задачі.

Для реалізації 2-го етапу існують багато методів уточнення коренів, наприклад, метод половинного ділення (метод бісекції, метод дихотомії), метод хорд,

7

метод січних, метод Ньютона (метод дотичних), модифікований метод Ньютона, метод простої ітерації тощо.

Коротко опишемо алгоритм найбільш простого і надійного метода уточнення коренів, а саме, метода половинного ділення, який нижче буде реалізова-

но у вигляді програми-функції користувача. З початку відрізок [a; b] локалізації

кореня рівняння f (x) = 0

ділимо навпіл, тобто знаходимо точку

a + b

. Якщо

2

f

a + b

= 0 , то ця точка є коренем цього рівняння. Якщо f

a + b

¹ 0 , то виби-

2

2

раємо ту з половин a;

a + b

або

a + b

; b , на кінцях якої функція f (x) має

2

2

значення протилежних знаків. Далі новий звужений відрізок локалізації [a1; b1]

знову ділимо навпіл і здійснюємо ті ж самі операції. Процес можна закінчувати,

якщо, наприклад, на n -му кроці довжина відрізка [a n ;bn ], стає меншою за за-

дану точність розрахунку ε , тобто виконуватиметься умова: bn − a n < ε . Але,

крім виконання вищенаведеної умови, для отримання наближеного значення кореня рівняння доцільно одночасно перевіряти виконання ще однієї умови, а

саме, щоб модуль різниці між точками f (a n ) та f (bn ) при черговому набли-

женні став меншим за ε , тобто f (bn ) - f (a n ) < e , або щоб значення модуля фу-

ε

a

n

+ b

n

<

e

нкції f (x) в точці

x n

стало меншим за

, тобто

f

(рис. 1).

2

2

2

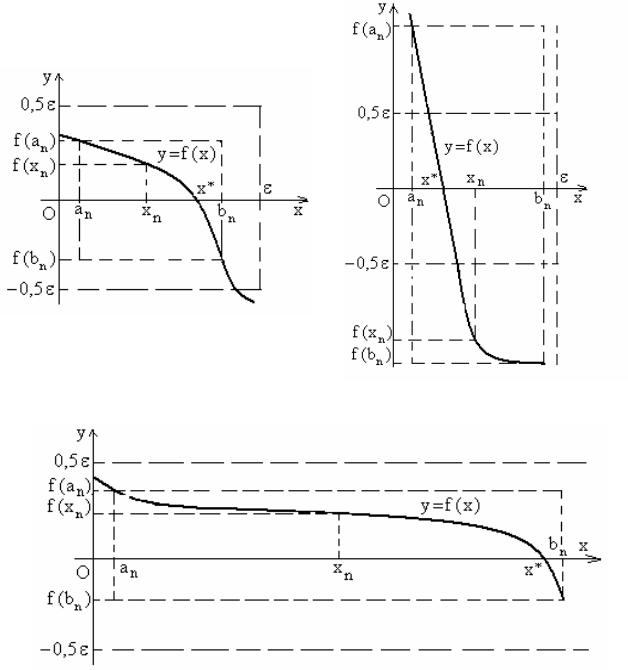
На рис. 2 – 3

маємо випадки поведінки функції f (x)

при наближенні до

кореня, для яких урахування лише однієї з цих умов може привести до отри-

мання помилкового значення кореня. Так, з рис. 2 видно, що величина bn − a n < ε , а x n знаходиться близько до точного кореня x* , в той же час вели-

чина f (bn ) - f (a n ) значно більше за ε , а величина f (x n ) значно більше за ε , 2

тобто x n не можна вважати коренем рівняння f (x) = 0 . З рис. 3 видно, що ве-

личина f (bn ) - f (a n ) < e , а величина f (x n ) < ε , але x n знаходиться далеко від

2

точного кореня x* , тобто не можна вважати x n коренем цього рівняння.

Описання алгоритмів інших методів уточнення коренів тут не наводимо,

але, в разі потреби, довідку про них можна знайти в багатьох довідниках і під-

ручниках з чисельних методів, зокрема в [10].

8

Рис. 1

Рис. 2

Рис. 3

В системі Mathcad обчислення наближеного кореня рівняння f (x) = 0 мо-

жна здійснювати за допомогою наступних інструментів:

1)Вбудованої функції root з чотирма аргументами, в якій реалізовано метод половинного ділення: root(f (x), x,a, b) , де f (x) – функція однієї змінної, що

визначає рівняння; x – змінна; a , b – границі відрізку локалізації. Має ви-

конуватися умова: f (a) × f (b) < 0 ;

9

2) Вбудованої функції root з двома аргументами, в якій реалізовано метод січних: root(f (x), x) , де f (x) – функція однієї змінної, що визначає рівняння; x – змін-

на. В програмі попереду функції root має стояти початкове значення змінної x .

3)Блокової структури Given – Find, у якій реалізовано один з градієнтних методів. В програмі попереду блокової структури має стояти початкове значення аргументу функції Find.

4)Вбудованої системи програмування Mathcad.

Крім того, для обчислення усіх коренів алгебраїчного рівняння Pn (x) = 0 ,

де його ліва частина має вигляд: Pn (x) = a 0 + a1 × x + a 2 × x 2 + ... + a n × x n , можна використовувати вбудовану функцію polyroots (a) , де a – вектор коефіцієнтів

алгебраїчного многочлена Pn (x) . Ця функція реалізована в двох варіантах: за допомогою метода Лагерра (LaGuerre) та метода парної матриці (Companion matrix). За замовчуванням використовується метод Лагерра. При необхідності можна змінити метод реалізації в контекстному меню функції polyroots (a) .

Слід зауважити, що точність обчислення кореня за допомогою вбудованих функцій root, polyroots задається значенням системної змінної TOL. Корінь вва-

жається знайденим, якщо при черговому наближенні x n значення модуля фун-

кції f (x n ) стає меншим значення змінної TOL , тобто має виконуватися умова: f (x n ) < TOL . Значення системної змінної TOL за замовчуванням дорівнює 0,001.

Це значення можна змінити за власним бажанням (збільшити або зменшити). Якщо значення змінної TOL зменшити, то процес уповільниться, але відповідь буде більш наближена до точного кореня. Для зміни значення TOL необхідно в меню Math (Математика) вибрати команду Options (Параметры). На вкладці Built-In Variables (Переменные) діалогового вікна Math Options внести необхідні зміни.

Аналогом системної змінної TOL у випадку використання блокової структури Given – Find є системна змінна CTOL .

Для визначення коренів рівняння f (x) = 0 , де функція f (x) задана таблицею, можна запропонувати наступну методику:

·побудувати для цієї функції інтерполяційну модель, наприклад, кубічну сплайн-інтерполяційну функцію за допомогою вбудованої функції interp або модель лінійної інтерполяції за допомогою вбудованої функції linterp (див. розділ 4);

·обчислити корені цієї інтерполяційної моделі за допомогою одного з вищенаведених методів розв’язання нелінійних рівнянь;

·вважати, що отримані корені є наближеними з заданою точністю значеннями коренів функції f (x) , що задана таблицею.

10

Висновки і поради. Найпростішим і найнадійнішим методом розв’язання нелінійних рівнянь є метод половинного ділення. Він має такі суттєві переваги над іншими методами:

∙невимогливість до виду функції, яка може мати точки розриву, точки, в яких невизначена похідна функції, декілька екстремумів (в таких випадках більш примхливі методи не спрацьовують);

∙простота комп’ютерної реалізації.

До недоліків методу половинного ділення можна віднести:

∙необхідність завжди задавати дві границі відрізку локалізації;

∙нечутливість до коренів парної кратності, але такі випадки – велика рідкість;

∙відносно повільна збіжність в порівнянні з іншими методами, але при потужностях сучасних комп’ютерів цей недолік стає другорядним.

Слід підкреслити, що недоліки цього методу на сучасному етапі розвитку комп’ютерної техніки є незначними в порівнянні з його перевагами.

Таким чином, для розв’язання нелінійного рівняння f (x) = 0 в середовищі

Mathcad можна порадити здійснити такі кроки:

∙побудувати графік функції та візуально визначити границі відрізків локалізації коренів рівняння;

∙отримати наближені значення коренів рівняння за допомогою однієї з функцій, побудованих на базі метода половинного ділення: вбудованої функції root з чотирма аргументами або запропонованої програми-функції користувача MPD;

∙ якщо функція f (x) є алгебраїчним многочленом, то наближені значення

всіх коренів рівняння має сенс отримувати за допомогою вбудованої функ-

ції polyroots;

∙якщо функція в деяких точках тільки торкається осі абсцис, не перетинаючи її (корні парної кратності), то значення коренів в цих точках можна отрима-

ти за допомогою вбудованої функції root з двома аргументами.

Нижче наведено приклади розв’язання нелінійних рівнянь з точністю до 0,001 за допомогою вищенаведених інструментів.

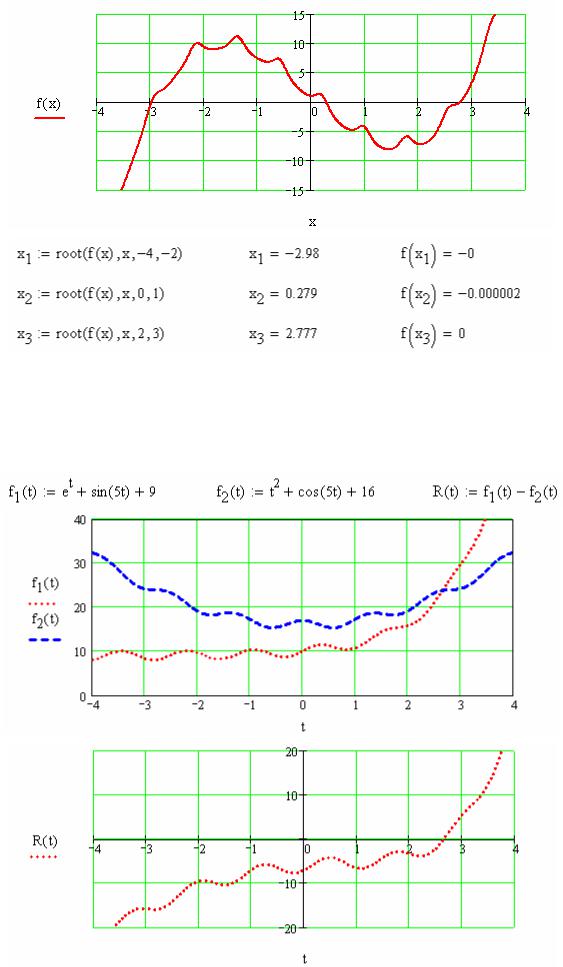
Задача 1. Знайти дійсні корені рівняння x3 − 8x + esin 8x = 0 за допомогою вбудованої функції root з чотирма аргументами.

Розв’язання задачі

11

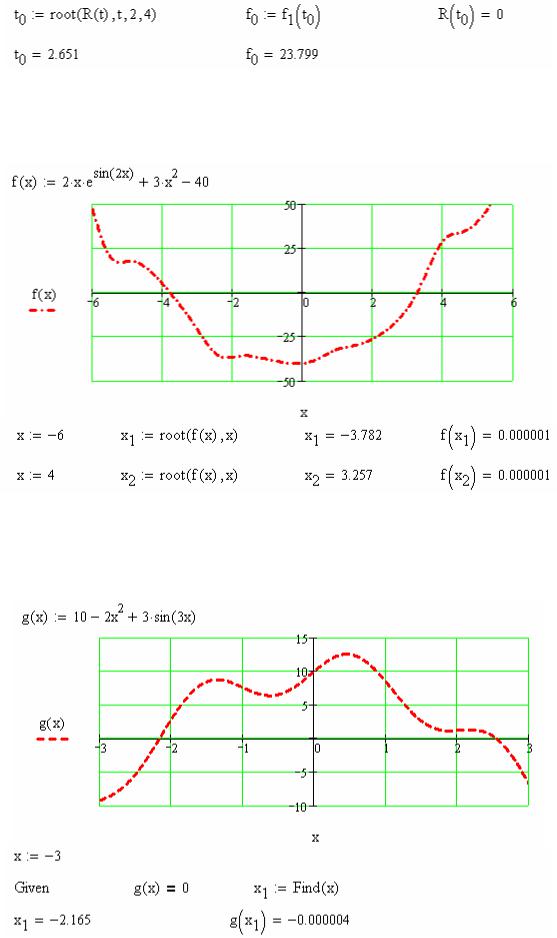
Задача 2. Знайти за допомогою вбудованої функції root з чотирма аргументами координати точки перетину двох функцій f1 (t) = et + sin 5t + 9 і f2 (t) = t 2 + cos5t + 16 .

Розв’язання задачі

12

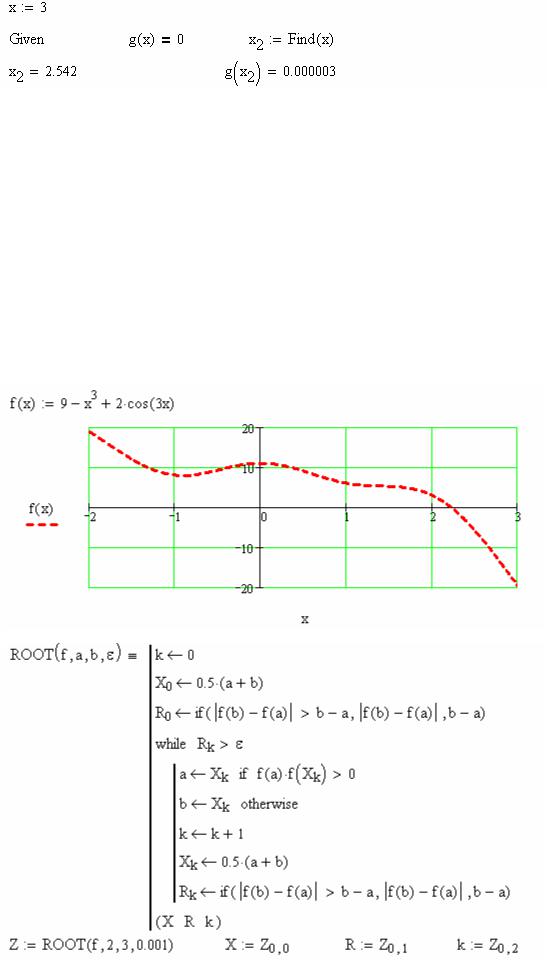
Задача 3. Знайти дійсні корені рівняння 2xesin 2x могою вбудованої функції root з двома аргументами.

Розв’язання задачі

Задача 4. Знайти дійсні корені рівняння 10 - 2x 2 гою блокової структури Given – Find.

Розв’язання задачі

+ 3x 2 − 40 = 0 за допо-

+ 3 × sin 3x = 0 за допомо-

13

Задача 5. Знайти дійсні корені рівняння 9 - x3 + 2 × cos 3x = 0 за допомогою програми-функції користувача ROOT.

Розв’язання задачі

Розв’язання задачі пропонується здійснити за допомогою програми-функції користувача ROOT(f , a, b, ε) , реалізованої на основі метода половинного ділення, де f

– ім’я функції, що визначає рівняння f (x) = 0 , a, b – границі відрізка локалізації кореня, ε – задана точність розрахунку. В програмі-функції реалізована перевірка обох вищезгаданих умов доведення наближеного значення кореня до заданої точності. На виході спостерігаємо процес прямування наближеного кореня (елементи масиву X) до значення точного кореня, а також одночасно процес зменшення похибки (елементи масиву R) до значення ε . Параметр k визначає кількість ітерацій, які маємо здійснити для доведення значення кореня до заданої точності ε .

14

Задача 6. Обчислити дійсні корені двох рівнянь x 2 - e0,5×x + 2 = 0 і 2 x 2 - e0,7×x + 2 = 0 за допомогою програми-функції користувача MPD.

Розв’язання задачі

Розв’язання цієї задачі здійснюється за допомогою ще однієї програми-функції користувача MPD(f ,a, b,ε) , реалізованої також на основі метода половинного ділення, де f – ім’я функції, що визначає рівняння f (x) = 0 , a, b – границі відрізка локалізації кореня, ε – задана точність розрахунку. Зверніть увагу на простоту реалізації програми-функції MPD: вона складається лише з одного оператора циклу while.

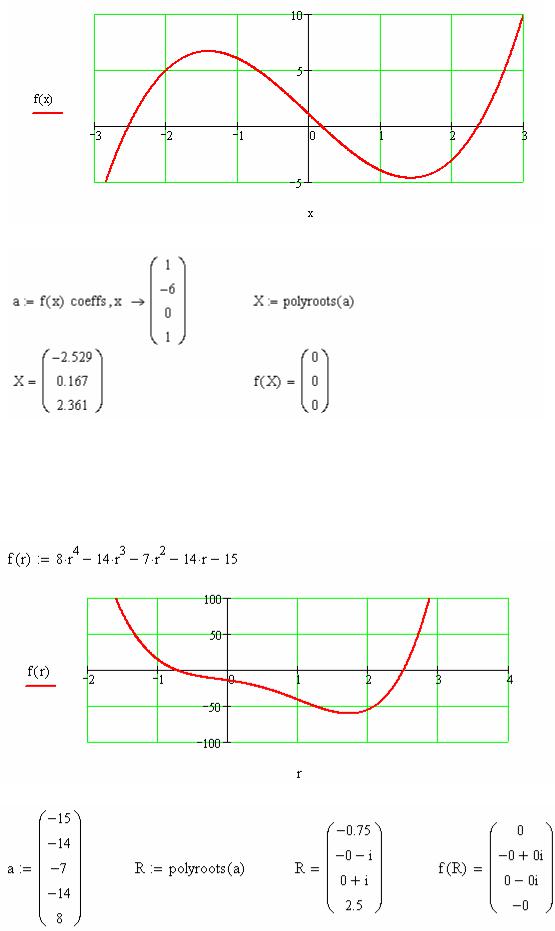
Задача 7. Знайти усі корені алгебраїчного рівняння x3 - 6 × x +1 = 0 за допомогою вбудованої функції polyroots.

Розв’язання задачі

15

Задача 8. За допомогою вбудованої функції polyroots знайти всі нулі алгебраїчного многочлена P4 (t) = 8 t 4 −14t3 − 7 t 2 − 14 t −15 .

Розв’язання задачі