Лекции Обчислювальна техн_МТ-3 / Тема 02 / Тема 02

14

Тема 2. Інтерполяція

ТЕМА 2

ЦІЛЬ ЛЕКЦІЇ

• викласти основні положення інтерполяції;

• показати різницю між апроксимацією і інтерполяцією;

• навести функції інтерполяції в програмному комплексі MathCAD;

• дати приклад інтерполяції

Ключові слова: інтерполяція, інтерполяційний многочлен, екстраполяція, інтерполяційні функції MathCAD

1.1.3. Інтерполяція

У задачах теорії споруд постійно стикаємося з необхідністю обчислення значень функції заданою таблицею в точках, не співпадаючих з фіксованими в таблиці. Типовим прикладом є обчислення ординат лінії впливу в тих точках де прикладаються зосереджені сили. Ця рутинна нудна операція може бути повністю автоматизована, якщо удатися до інтерполяції.

	Визначення. Інтерполяція є наближене представлення функції заданою таблицею. Кінцевою метою інтерполяції є обчислення значень функції в точках, які не співпадають з фіксованими в таблиці.

З приведеного визначення, очевидно, що задача інтерполяції співпадає із задачею апроксимації. Загалом це так, але у пошуках функції інтерполяції потрібно додатково задовольнити важливій умові: шукана функція має єдиним чином проходити через точки інтерполяції.

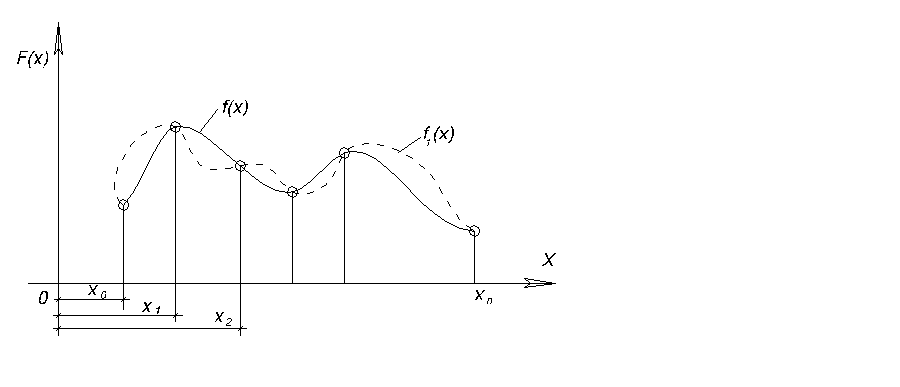
Геометрично, задача інтерполяції для функції однієї змінної означає побудову кривої, що проходить через задані точки (рис.1.3). Зверніть увагу, що поки задачі інтерполяції і апроксимації абсолютно ідентичні. Проте вже з рисунка інтуїтивно ясно, що через задані точки можна провести незліченну безліч різних кривих. Таким чином, задача відшукання функції f(x) по кінцевому числу її значень стає невизначеною.

 f(x) _ _ _ Рис.1.3. Функції інтерполяції

Ця задача стає однозначною, якщо для функція інтерполяції f(x) заданої своїми n +1 значеннями вибрати многочлен ступеня не вище n, такий, що

, (1.6)

де - задані n +1 значень функції.

Многочлен задовольняючий цим умовам, називається інтерполяційним многочленом. Зверніть увагу, що сплайн, за визначенням, задовольняє умовам (1.6).

Якщо аргумент інтерполяції х знаходиться за межами відрізка інтерполяції, то задача визначення значень функції в довільних точках відрізка називається екстраполюванням

4. Функції інтерполяції програмного комплексу MathCAD

У програмному комплексі MathCAD є стандартні функції лінійної і сплайнової інтерполяції.

Лінійна інтерполяція

Функція, що обчислює за лінійною інтерполяцією для довільного аргументу х значення функції F(x), заданої своїми значеннями у фіксованих вузлах, має вид:

linterp(vx, vy, x),

де vx - вектор координат вузлів;

vy - вектор значень функції у вузлах;

x - координата для якої потребується обчислити значення функції.

Сплайнова інтерполяція

Стандартна функція програмного комплексу MathCAD, яка обчислює в довільних точках інтерполяції за сплайном значення функції F(x),, заданої у фіксованих вузлах, має вид:

interр(S, vx, vy, x),

де vx - вектор координат вузлів;

vy - вектор значень функції в узлах;

x - координата для якої потребується обчислити значення функции.

S= cspline(vx, vy) – обчислює коефіцієнти сплайна;

1.1.4 Приклад інтерполяції

Приклад 1.2

Розглядається бездіфрагмова прогонова будова з прольотом м. У перерізі прогонової будови 9 балок. Ширина полиці балки м. Для крайньої балки, досить точним дискретним методом, у середньому перерізі, отримано 9 ординат лінії впливу тиску:

Lv^T = [0.367 0.233 0.148 0.094 0.060 0.039 0.026 0.019 0.016]. Крок ординат є x_b=b=2,1 м.

Потрібно побудувати сплайнову функцію, що інтерполює лінію впливу тиску і знайти коефіцієнти поперечного розподілу двох колон навантаження А11 для =1,85м, де х₁ - відстань від початку координат до лівого крайнього вантажу навантаження А11 (рис. 1.4). Три інших координати отримуються за загальними правилами розміщення в поперечному перерізі прогонової будови навантаження А11:

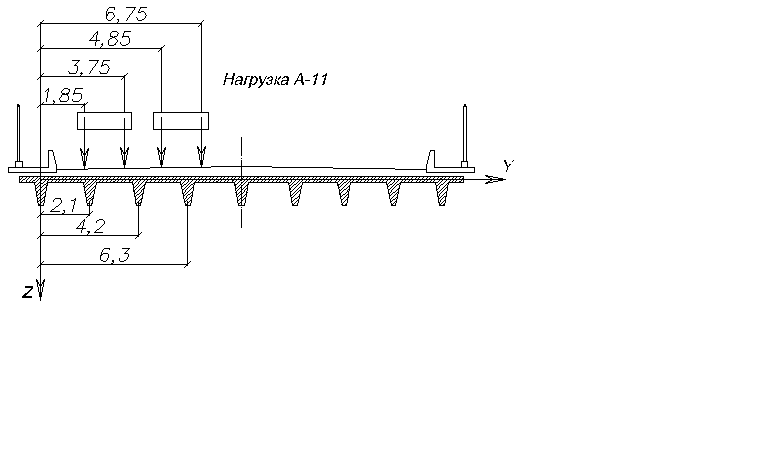
x₂ = x₁ + 1,9 = 3,75 м; х₃ = х₂ + 1,1 = 4,85 м;

х₄ = х₃ + 1,9 = 6,75 м

Рис.1.4. Схема розміщення навантаження на прогоновій будові

На рис. 1.5 показано визначення сплайнового інтерполяційного поліному P(x) в системі MathCAD.

Коли інтерполяційний поліном визначено, процедура вирахування ординат в заданих точках стає зовсім простою – достатньо підставити задані координати в отриману функцію P(x) (На рис. 1.5. функція позначена Ps(x)).

Далі, в термінах MathCAD, наводиться приклад інтерполяції сплайном лінії впливу тиску, заданої таблицею.

В прикладі (рис.1.7) також наводиться процедура використання отриманого сплайна для обчислення коефіцієнта поперечного розподілу.

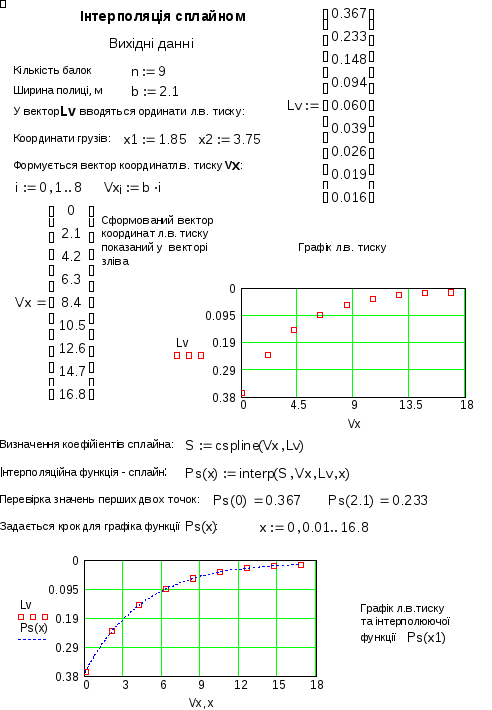
Рис. 1.6 Інтерполяція сплайном функції заданої таблицею

На рис. 1.7. показано обчислення коефіцієнту поперечного розподілу шляхом застосування отриманої вище функції інтерполяції ординат лінії впливу тиску на балку

Рис. 1.7 Обчислення КПР за сплайновою інтерполяцією лінії впливу тиску