Курсовая работа / Вариант 10 - Браженков - Сатановская - 2004 / вар10

Российский химико-технологический университет

им. Д.И. Менделеева

кафедра сертификации и стандартизации

Курсовая работа на тему:

«Статистическая обработка экспериментальных

данных при сертификации продукции.

Оценивание распределений и их параметров».

Вариант №10

Выполнила: студентка 5 курса

ф-та КХТП

группы К-53 СатановскаяМ.М.

Проверил: Браженков А.И.

Москва 2004г.

Цель работы:

Работа посвящена наиболее важным методам обработки экспериментальных данных, а именно, оцениванию распределений и их параметров и проверки гипотез о распределениях.

Содержание работы:

1. Найти оценки математического ожидания и дисперсии случайной величины Х.

2. Найти доверительные интервалы для математического ожидания и

дисперсии, соответствующие заданной доверительной вероятностью.

(1-α)=0,85.

3. Оценить вероятность попадания случайной величины Х в заданный

интервал (0,8÷1,1).

4. Для этой вероятности найти доверительный интервал, соответствующий

заданной доверительной вероятности (1-α) = 0,8.

5. Построить гистограмму и эмпирическую функцию распределения

случайной величины Х.

6. Найти и построить доверительные области для плотности

распределения f(x) и функции распределения F(x), соответствующие

заданной доверительной вероятности: f(x)=> (1-α) = 0,85

F(x)=> (1-α) = 0,9.

7. Сгладить гистограмму и эмпирическую функцию распределения

подходящим законом распределения.

8. Используя критерий согласия χ² и теорему Колмогорова, проверить

правдоподобие гипотезы о совпадении выбранного закона

распределения с истинным законом при заданном уровне значимости: α=0,01.

Задание:

Фиксируется отклонение скорости самолета (в м/с) от нормативной. Данные по ста полетам приведены в таблице при полете по маршруту.

Таблица №1:

2,7	-10,95	17,1	7,95	6,45	0,15	11,25	-24,25	11,85	20,4
4,65	-0,9	20,7	10,95	15,6	3,75	26,55	-2,4	15,9	4,35
17,85	31,35	-10,65	-3,6	21,45	8,4	-6,45	23,1	28,05	13,8
60,3	-3,45	20,85	-10,5	16,05	24,75	4,05	-5,85	-20,25	5,7
12,3	25,95	-2,25	0,15	51,75	4,5	-1,05	-9,15	37,05	3,9
16,35	23,25	4,65	6	20,7	-0,15	-3,15	-0,15	-6,45	-16,95
19,05	12,9	8,7	16,05	22,05	7,35	-34,95	-0,75	18,5	5,7
5,55	13,8	3,75	-0,15	22,95	20,55	11,25	28,65	10,5	-9,6
2,4	28,05	19,35	13,35	-0,15	22,2	-1,2	8,25	-23,25	-12,45
18,9	-5,55	9,75	34,65	10,2	-8,94	14,25	28,2	-3,6	-13,35

Решение:

1.Найдем точечные оценки математического ожидания и дисперсии, учитывая, что n=100.

Математическое ожидание:

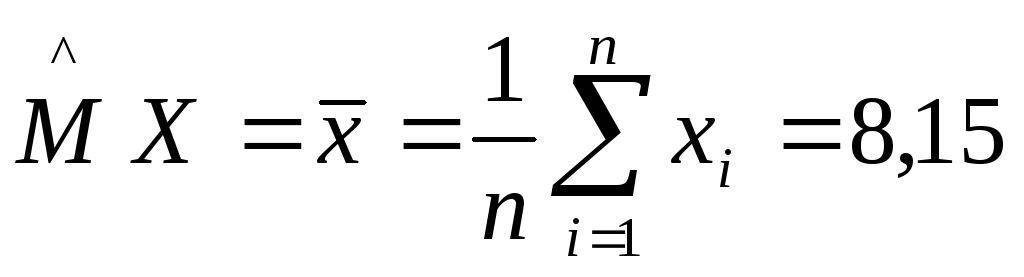
Дисперсия:

• исправленная:

• выборочная:

2. Рассчитаем доверительные интервалы для математического ожидания и дисперсии, предварительно задав доверительную вероятность (1-). Пусть (1-) = 0,85. Тогда по таблице значений функции Лапласа находим и, следовательно, искомые доверительные интервалы будут иметь вид:

• для математического ожидания:

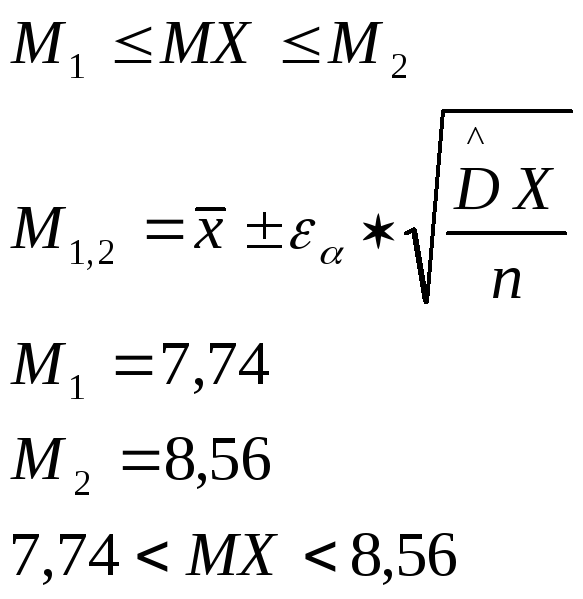
• для дисперсии:

3. Находим точечную оценку вероятности попадания случайной величины X в интервал (0,8÷1,1) = (6,52÷8,96). Так как в этот интервал попало m=5 экспериментальных значений, то искомая оценка будет равна:

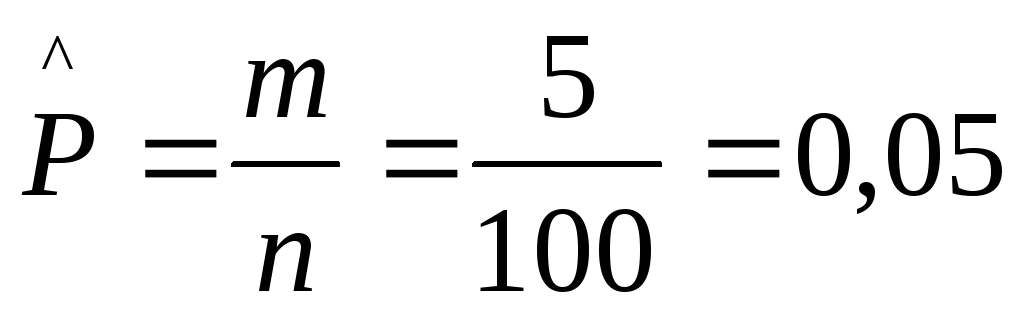
4. Рассчитываем доверительный интервал для вероятности Р, оцененной в предыдущем пункте. Пусть в этом случае доверительная вероятность равна (1-) = 0,8. Тогда =1,29 , и искомый интервал имеет вид :

5. Для построения гистограммы Г(x) заключаем все экспериментальные данные в интервал (0; 100) и разбиваем его на 10 равных разрядов, каждый длиной 10. Для каждого разряда рассчитываем:

• значение гистограммы Г(x):

, где - число экспериментальных точек, попавших в этот разряд , а - его длина.

• частоты попадания экспериментальных точек в разряды гистограммы:

Интервалы (разряды)	ni	частота попадания случайной величины Х в интервал	Значение гистограммы Г(х)
[0;10)	21	0,21	0,021
[10;20)	22	0,22	0,022
[20;30)	18	0,18	0,018
[30;40)	3	0,03	0,003
[40;50)	0	0	0
[50;60)	2	0,02	0,002
[60;70)	0	0	0
[70;80)	0	0	0
[80;90)	0	0	0
[90;100)	0	0	0

Гистограмма №1:

Из гистограммы№1 видно, что распределение нормальное.

Соответствующую эмпирическую функцию рассчитываем по формуле:

,где - число экспериментальных точек, лежащих левее х.

Гистограмма №2:

6. Находим доверительные области для плотности распределения f(x) и функции распределения F(x).

На каждом разряде находим доверительную область для вероятности попадания исходной величины X в этот разряд. Вычисляем доверительную вероятность по формуле из пункта 4 с заменой величин соответственно на . В данном случае общее число разрядов r = 10 плюс 2 полубесконечных разряда , r = 12. Выбираем доверительную вероятность (1-), равную 0,9 , из условия:

и, используя таблицу значений функции Лапласа, находим = 2,64.

i = 1...r

плотность на i-ом разряде;

доверительные границы для плотности , которая находится по формуле:

длина разряда.

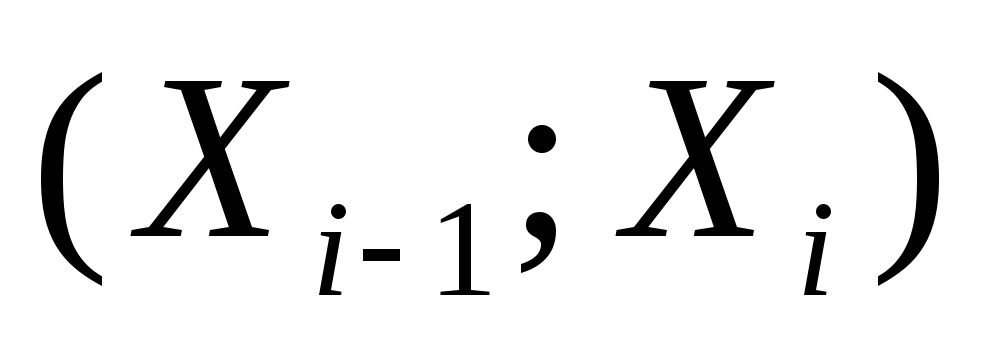
разряд	доверительные границы для плотности распределения f(x)
0	0	0,006943
0	0	0,006943
[-60;-48)	6,54E-06	0,007356
[-48;-36)	2,95E-06	0,007219
[-36;-24)	2,53E-05	0,007767
[-24;-12)	1,14E-05	0,007492
[-12;0)	0,000106	0,00867
[0;12)	0,000537	0,011075
[12;24)	9,03E-05	0,008533
[24;36)	2,53E-05	0,007767
[36;48)	3,4E-05	0,007902
0	0	0,006943
0	0	0,006943

(см. рис. 3)

Графической оценкой функции распределения F(x) является эмпирическая функция распределения:

, где - число экспериментальных точек, лежащих левее x.

По таблице распределения величины (распределение Колмагорова) находим ее величину, соответствующую коэффициенту доверия (1-) = 0,8. Она равна =1,08. Затем рассчитываем доверительную область для функции распределения F(x):

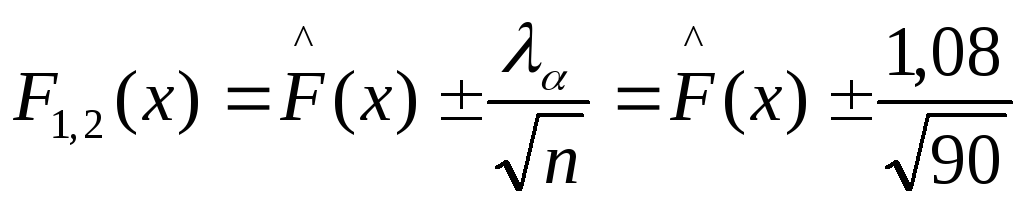
График этой области представлен на рис. 4

7. Из формы гистограммы следует, что гипотетическим распределением может быть нормальное распределение с функцией:

график представлен на рис. 5

8. Для проверки гипотезы выберем уровень значимости α = 0,01 и используем критерий согласия . Экспериментальное значение

вычисляется по формуле:

где для нормального распределения определяется следующим образом:

Экспериментальное значение,согласно вышеуказанной формуле

= 14,56

Значение зависит от двух величин (α,s). Уровень значимости α = 0,01; число степеней свободы:

S = r – 1 – k

k = 2 , так как нормальное распределение, тогда

s = 12-1-2 = 9

Значит, теоретическое значение (по табл.)

Таким образом,

<

гипотеза является правдоподобной

Проверим эту же гипотезу с помощью критерия Колмогорова. Максимальное различие между гипотетической и эмпирической функциями распределения равно в данном случае:

Экспериментальное значение критерия Колмогорова равно:

Гипотетическое значение этого критерия при уровне значимости α = 0,01 (по таблице Колмогорова) равно:

1,63

Таким образом, , следовательно, гипотеза является правдоподобной также и по критерию Колмогорова.

10