Курсовая работа / Вариант 13 - 2004 / вар13

Вариант 13

Измерено давление в 80 пневматиках. В таблице приведены отклонения давления от номинального (в 10³ Па).

-9,6	5,1	-6,9	-6,6	-21,8	6,4	-17,8	-3,4
-5,6	5	-6,6	-17,5	-3,5	-8,6	-3,6	-8,8
-19,8	12,8	-27,7	-6,3	-10,9	-7	3,8	-4,4
-15,2	4	6,3	20,3	3,3	-7,7	-3	-18,6
-14	8,4	12,7	-1,5	-2,4	-11	-29,6	-5,2
-16,8	-7,8	-8,7	-0,3	-1,4	15,9	0,31	-5,1
10	13	0,1	0,1	-23,3	-5,9	1,3	-17,4
1,9	6,8	-7,9	5,6	15,6	11,8	-17,8	8,8
-0,2	-11,6	8,3	-0,2	15	1,6	0,25	4,6
8,7	0,7	-2,2	-7,3	-16,8	0,21	-5	-12,2

Цель работы

Работа посвящена наиболее важным методам обработки экспериментальных данных, а именно оцениванию распределений и их параметров и проверке в распределениях.

Содержание работы

1. Найти оценки математического ожидания и дисперсии случайной величины Х.

2. Найти доверительные интервалы для математического ожидания и дисперсии соответствующие заданной доверительной вероятности.

3. Оценить вероятность попадания случайной величины Х в заданный интервал.

4. Для этой вероятности найти доверительный интервал, соответствующий заданной доверительной вероятности.

5. Построить гистограмму и эмпирическую функцию распределения случайной величины Х.

6. Найти и построить доверительные области для плотности распределения f(x) и функции распределения F(X), соответствующие заданной области.

7. Сгладить гистограмму и эмпирическую функцию распределения подходящим законом распределения.

8. Используя критерии согласия χ² и Колмогорова проверить правдоподобие гипотезы о совпадении выбранного распределения с истинным законом при заданном уровне значимости.

Решение

1. Находим точечные оценки математического ожидания и дисперсии, учитывая, что n=100.

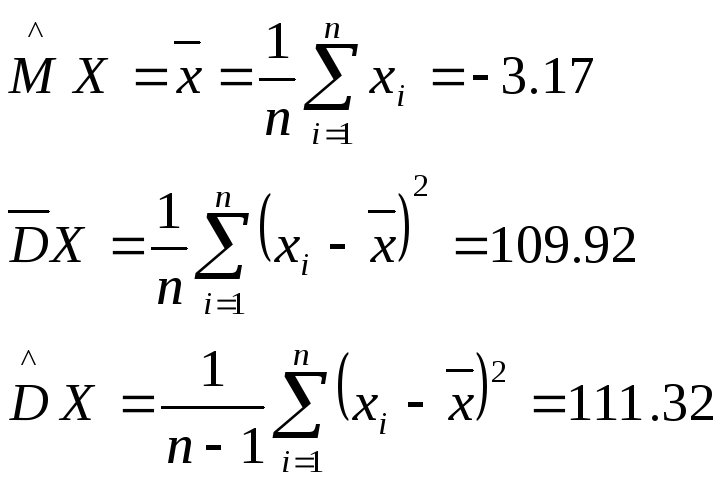
2. Рассчитываем доверительные интервалы для математического ожидания и дисперсии, предварительно задав доверительную вероятность (1-α)=0.75 . Тогда по формуле

и таблице Лапласа находим ε_α=1.152 и, следовательно, искомые доверительные интервалы будут иметь вид:

-4.53<MX<-1.81 93.95<DX<135.86

3. Находим точечную оценку вероятности попадания случайной величины Х в интервал . Т.к. в этот интервал попало m=4 экспериментальных значения, то искомая оценка будет равна:

4. Рассчитываем доверительный интервал для вероятности Р(х), оцененной в предыдущем пункте. Пусть в этом случае доверительная вероятность равна (1-α)=0,9. Тогда ε_α=1.65, а искомый интервал имеет вид

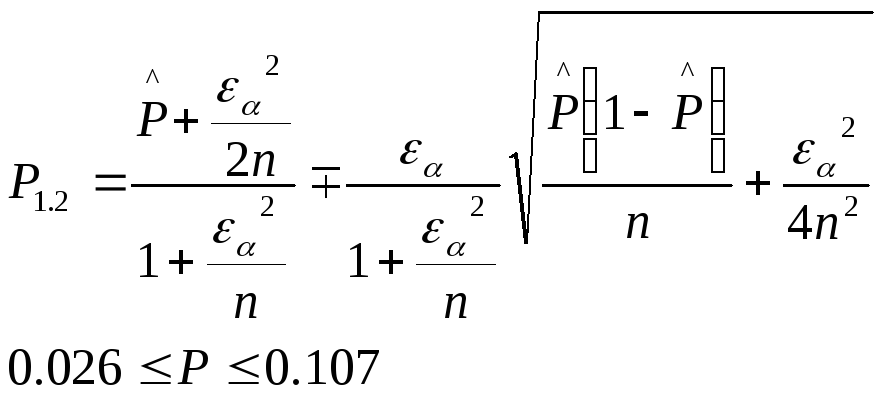
5. Для построения гистограммы Г(х) заключаем все экспериментальные данные в интервал (-30,21) и разбиваем его на 10 равных разрядов, каждый из которых длинной 5. Затем рассчитываем следующую таблицу:

Разряд (Xi-1;Xi)	Частота попадания случайной величины Х в разряд (Xi-1;Xi)	Значение гистограммы Г(х)
(-30;-25)	0,025	0,005
(-25;-20)	0,025	0,005
(-20;-15)	0,1125	0,0225
(-15;-10)	0,0625	0,0125
(-10;-5)	0,225	0,045
(-5;0)	0,15	0,03
(0;5)	0,175	0,035
(5;10)	0,125	0,025
(10;15)	0,0625	0,0125
(15;20)	0,0375	0,0075

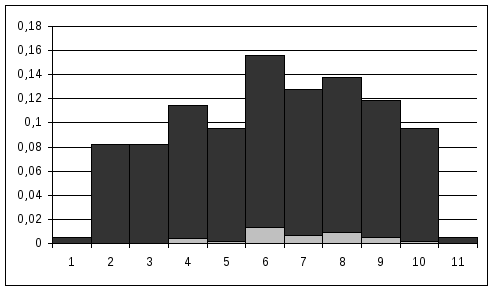
График гистограммы представлен на рис.1 Соответствующую эмпирическую функцию рассчитываем по формуле

Ее график представлен на рис. 2

6. Находим доверительные области для распределения f(х) и функции распределения F(х).

В данном случае общее число разрядов r равно 10 плюс два полубесконечных разряда, т.е. r=12. Если теперь выбрать доверительную вероятность (1-α) равную 0,85 то получим ε_α=2,5.

Результирующие доверительные границы для плотности f(х) на каждом разряде гистограммы представлены в таблице, а их графическое изображение на рис.2

Разряд (Xi-1;Xi)	Нижняя граница для плотности распределения f(x)	Верхняя граница для плотности распределения f(x)
(-30;-25)	0,000285	0,081454
(-25;-20)	0,000285	0,081454
(-20;-15)	0,004271	0,109931
(-15;-10)	0,00154	0,094112
(-10;-5)	0,013154	0,142788
(-5;0)	0,006886	0,12123
(0;5)	0,008839	0,128553
(5;10)	0,005097	0,113744
(10;15)	0,00154	0,094112
(15;20)	0,000608	0,085769

Далее по таблице распределения величины λ_α (распределение Колмогорова) находим ее величину, соответствующую коэффициенту доверия (1-α)=0,95. Она равна λ_α=1,4

Затем по формуле

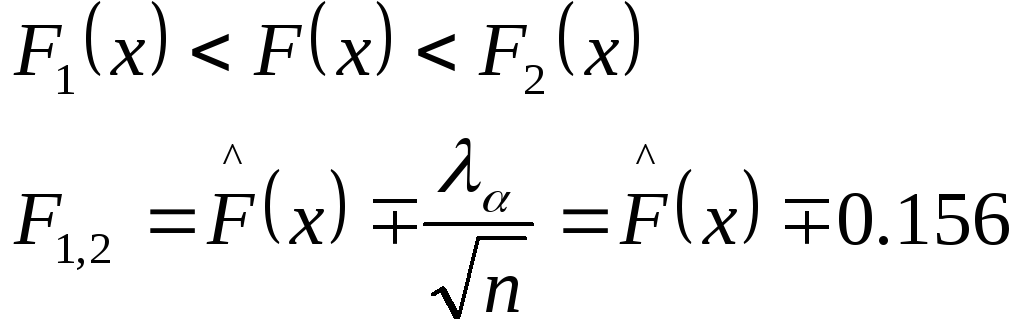
рассчитываем доверительную область для функции распределения F(х).

График этой области представлен на рис.3

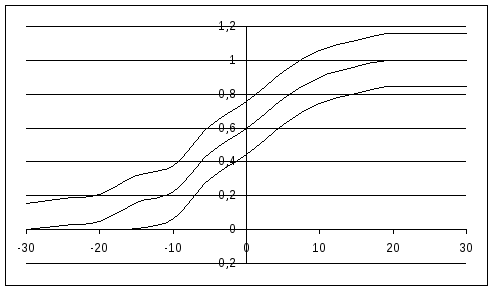
7. На формы гистограммы следует, что гипотетическим распределением может быть экспоненциальное распределение с функцией

и с плотностью

где– оценка неизвестного значения λ_α. Т.к. , то и, следовательно

Возможен случай, когда из формы гистограммы следует, что гипотетическим распределением может быть нормальное распределение с функцией

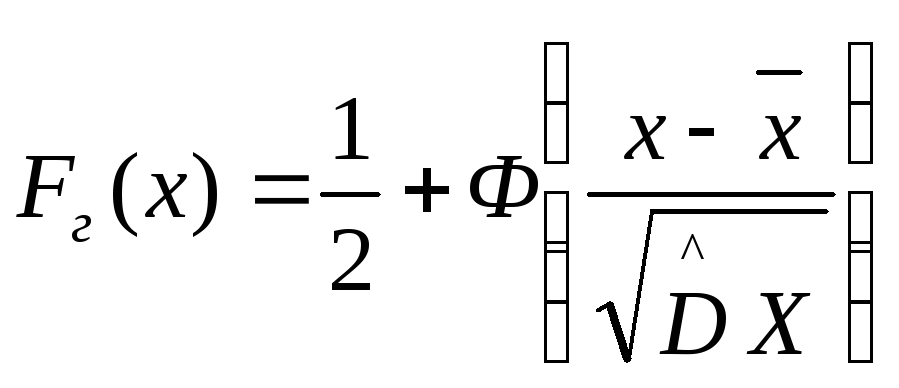
и с плотностью

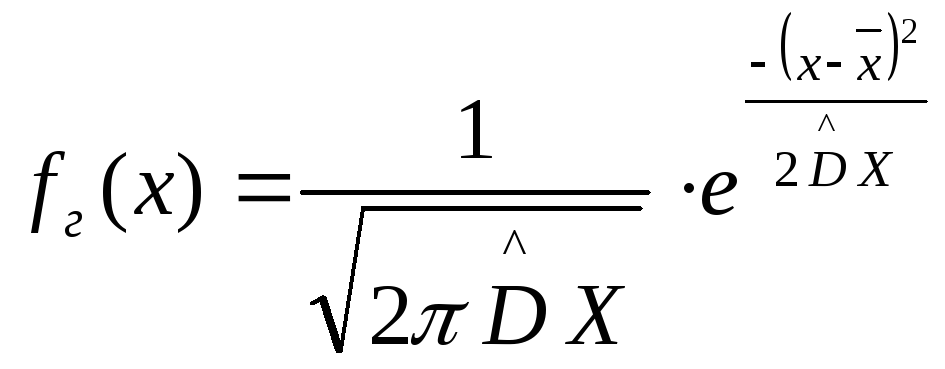
где F(u)- функция Лапласа. – исправленная дисперсия.

8. Для проверки гипотезы H₀:F(x)=F_Г (х) выбираем например уровень значимости α=0,05 и используем вначале критерий согласия χ². Его экспериментальное значение, согласно формуле

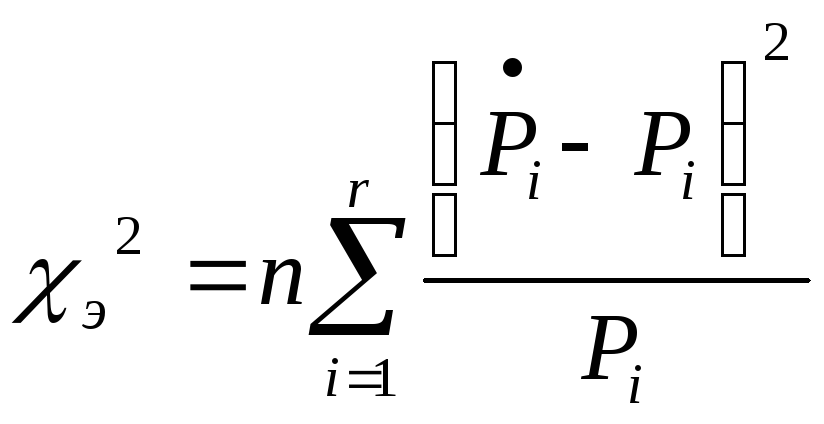
равно χ²_э=137.

А его гипотетическое значение при выбранном уровне значимости α=0,05 и числе степеней свободы s=12-1-1=10 согласно условию

равно χ²_α=18,3. Таким образом и следовательно гипотеза Н₀ по критерию согласия χ² не является правдоподобной.

Теперь проверим ту же самую гипотезу с помощью критерия согласия Колмогорова. Максимальное различие между гипотетической и эмпирической функциями распределения в этом случае равно (см. рис. 4)

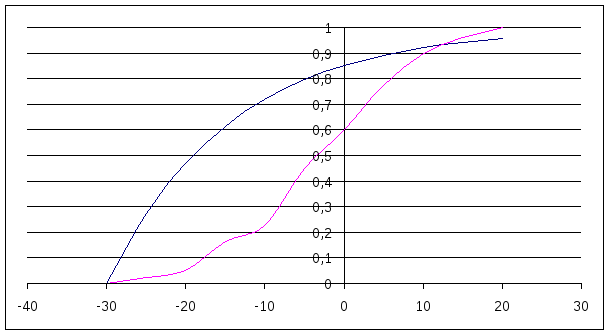
откуда получаем экспериментальное значение критерия Колмогорова:

Гипотетическое значение того же самого критерия при уровне значимости α=0,05 (см. табл. Колмогорова) равно λ_α=1,4. Таким образом и, следовательно, гипотеза Н₀ не является правдоподобной так же по критерию Колмогорова.