Министерство образования и науки РФ

Российский химико-технологический университет

им. Д.И. Менделеева

Кафедра «Стандартизация и сертификация»

Курсовая работа

по дисциплине:

«Основы метрологии, стандартизации и сертификации»

Вариант задания: 25

Проверил: Иванов В.В.

Выполнила: Балабаева Е.В.

Москва 2008

Вариант №25

В ста измеренных эталонах фиксировались ошибки измерительных приборов данного типа. Результаты измерения сведены в таблицу:

0,72	0,51	1,03	1,08	2,29	-0,98	-1,08	0,12	1,24	-0,83
1,19	1,22	1,15	0,91	-0,19	1,78	0,62	0,84	1,02	1,95
1,79	0,83	1,29	1,43	0,04	1,31	0,10	0,17	0,15	0,03
1,19	2,09	1,87	0,47	2,19	1,48	0,56	0,19	0,50	-0,69
0,74	2,24	0,71	-0,43	1,41	-1,57	1,51	-0,35	1,44	0,44
2,58	0,85	2,12	3,92	1,16	0,61	1,00	1,50	-0,88	0,37
2,09	-0,69	0,21	-0,19	0,37	-1,83	-0,27	0,68	0,75	-0,11
1,45	-0,04	1,06	1,19	1,75	1,36	-0,79	0,57	0,58	-0,73
0,54	2,62	1,48	1,94	0,79	-0,04	0,02	2,05	1,86	1,52
1,96	2,05	2,05	2,22	-0,53	1,09	-0,36	1,73	0,74	0,43

Содержание работы:

1. Используя табличные значения необходимо найти математическое ожидание и дисперсию (Mx, Dx).

2. Найти доверительный интервал для Mx, Dx, соответствующий доверительной вероятности (1 - )=0,85.

3. Оценить вероятность попадания случайной величины X в интервал

(0,8 1,1) .

4. Для этой вероятности (3) найти интервал, соответствующий коэффициенту доверия (1 - )=0,8.

5. Построить гистограмму и эмпирическую функцию распределения.

6. Найти и построить доверительные области для f(x), соответствующую коэффициенту доверия (1- )=0,85; и F(x), соответствующую коэффициенту доверия (1- )=0,9.

7. Сгладить гистограмму и эмпирическую функцию распределения подходящим законом распределения.

8. Используя критерий согласия и критерий Колмогорова проверить правдоподобие гипотезы о совпадении выбранного закона распределения с истинным законом при уровне значимости =0,01.

Решение:

1. Находим точечные оценки математического ожидания и дисперсии, учитывая, что n=100.

   Выборочное среднее: Выборочная дисперсия: Исправленная дисперсия:

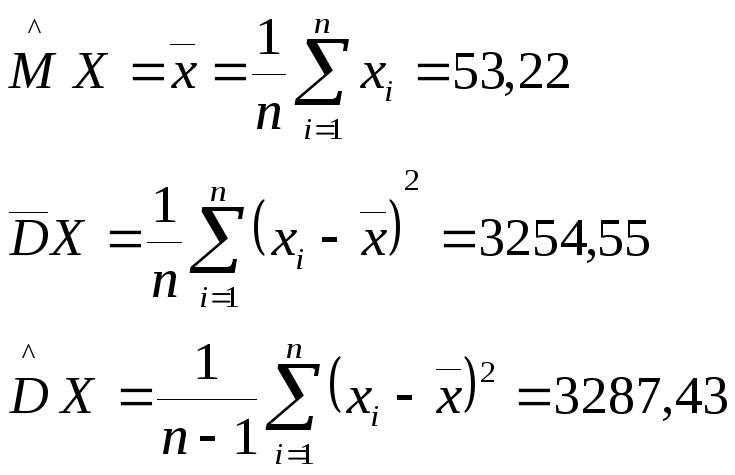
2. Рассчитываем доверительные интервалы для математического ожидания и дисперсии, предварительно задав доверительную вероятность (1-α)=0,95 . Тогда по формуле:

По таблице Лапласа находим ε_α=1,96.

Доверительный интервал для математического ожидания:

Mx₁ = 53,22 – 1,96ּ Mx₂=53,22 + 1,96ּ

Доверительный интервал для дисперсии:

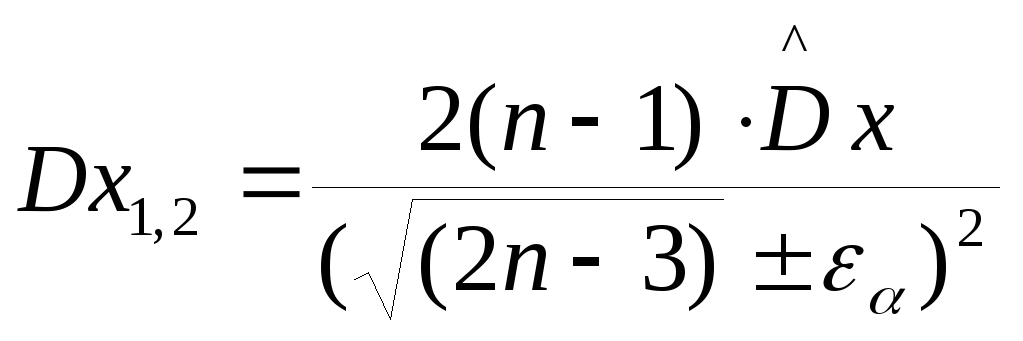
Dx₁ = = 2544,00 Dx₂= = 4463,74

следовательно, искомые доверительные интервалы будут иметь вид:

41,98  MX  64,44 2544,00  DX  4463,74

3. Находим точечную оценку вероятности попадания случайной величины Х в интервал . Т.к. в этот интервал попало m=10 экспериментальных значений, то искомая оценка будет равна:

4. Рассчитываем доверительный интервал для вероятности Р(х), оцененной в предыдущем пункте. Пусть в этом случае доверительная вероятность равна (1-α)=0,9. Тогда ε_α=1,65, а искомый интервал имеет вид:

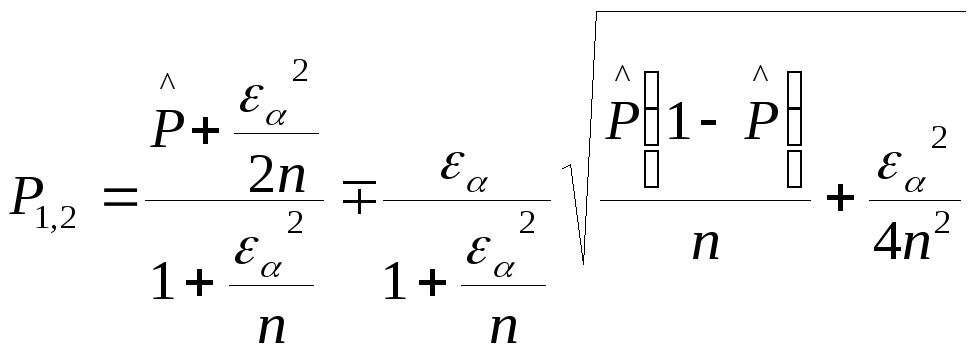
5. Построим гистограмму и эмпирическую функцию распределения случайной величины Х.

1) Для построения гистограммы Г(х) заключаем все экспериментальные данные в интервал (0 ; 316) и разбиваем его на 8 равных разрядов, каждый из которых длинной 39.5.

Значение гистограммы Г(x) находим по формуле : ,

где - число экспериментальных точек, попавших в этот разряд ;

- его длина.

_{величина интервала:}

_{количество разрядов: k = 8}

величина разряда:

Затем рассчитываем следующую таблицу:

№ разряда	Разряд		Частота попадания случайной величины X в разряд		Значение гистограммы Г (х)
	нижняя граница	верхняя граница
			ni	ni/n
1	0	39.5	55	0,02	0,028
2	39.5	79	22	0,1	0,138
3	79	118.5		0,17	0,234
4	118.5	158	27	0,27	0,372
5	158	197.5	24	0,24	0,331
6	197.5	237	17	0,17	0,234
7	237	276.5	2	0,02	0,028
8	276.5	316	1	0,01	0,014

График гистограммы представлен на рис.1: