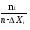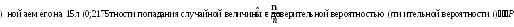Задание.

Производится исследование точности измерения дальности с помощью радиальности. Зарегистрированы следующие ошибки показаний прибора (в метрах):

-10	4	6	42	20	3	-8	0	-30
-18	0	50	10	-3	-32	-14	22	-40
-58	-5	-14	3	-7	52	0	20	-30
10	-21	-43	16	-12	-3	14	-10	20
0	2	0	14	-45	-7	38	-3	15
-2	-5	-24	5	0	-8	2	10	0
-32	3	3	-27	30	-14	50	-4	31
-40	10	-10	35	0	37	1	12	15
-58	4	-12	30	40	2	10	-3	-15
-10	-1	47	32	48	5	15	2	0

1. Найти оценки математического ожидания и дисперсии случайной величины Х.

2. Найти доверительные интервалы для математического ожидания и дисперсии, соответствующие заданной доверительной вероятности ((1 - α) = 0,85).

3. Оценить вероятность попадания случайной величины Х в заданный интервал (0,7 - 1) .

4. Для этой вероятности найти доверительный интервал, соответствующий заданной доверительной вероятности ((1 - α) = 0,90).

5. Построить гистограмму и эмпирическую функцию распределения случайной величины Х.

6. Найти и построить доверительные области для плотности распределения f (x) и функции распределения F (x), соответствующие заданной доверительной вероятности ((1 - α) = 0,90).

7. Сгладить гистограмму и эмпирическую функцию распределения подходящим законом распределения.

8. Используя критерий согласия χ² и критерий Колмогорова, проверить правдоподобие гипотезы о совпадении выбранного закона распределения с истинным законом распределения при заданном уровне значимости ( α = 0,05).

Решение.

Располагаем экспериментальные данные в порядке возрастания:

-58	-58	-45	-43	-40	-40	-32	-32	-30
-30	-27	-24	-21	-18	-15	-14	-14	-14
-12	-12	-10	-10	-10	-10	-8	-8	-7
-7	-5	-5	-4	-3	-3	-3	-3	-2
-1	0	0	0	0	0	0	0	0
0	1	2	2	2	2	3	3	3
3	4	4	5	5	6	10	10	10
10	10	12	14	14	15	15	15	16
20	20	20	22	30	30	31	32	35
37	38	40	42	47	48	50	50	52

1. Находим точечные оценки математического ожидания и дисперсии, учитывая, что n = 90, по формулам:

- для математического ожидания MX - выборочное среднее:

-для дисперсии DX – исправленная дисперсия:

- выборочная дисперсия – DX

2. Находим доверительные интервалы для математического ожидания и дисперсии для доверительной вероятности (1 - α) = 0,85.

1) 2Φ(ε_α) = 1 – α, Φ(ε_α) – функция Лапласа

Φ(ε_α) = (1 - α)/2 = 0,85/2=0,425

По таблице для функции Лапласа находим ε_α = 1,44

2) а) доверительный интервал для математического ожидания:

Mx1 = 2,0 – 1,44ּ Mx2 = 2,0 +1,44ּ

б) доверительный интервал для дисперсии:

Dx1 = = 446,10 Dx2= = 688,96

3. Вероятность попадания случайной величины Х в заданный интервал (0,7 - 1) 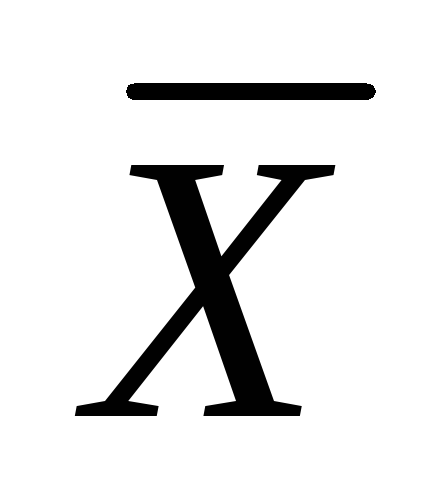, то есть 1,4 ≤ ≤ 2:

, m = 4 – число значений, попавшее в данный интервал,

n = 90 – общее число значений

4. Доверительный интервал для вероятности попадания случайной величины с доверительной вероятностью (1 - α) = 0,90:

2Φ(ε_α) = 1 – α, Φ(ε_α) – функция Лапласа

Φ(ε_α) = (1 - α)/2 = 0,90/2=0,45

По таблице для функции Лапласа находим ε_α = 1,65

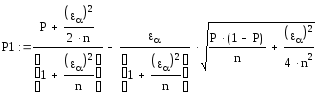
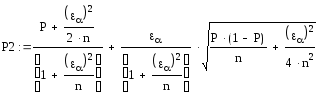
Р1 = 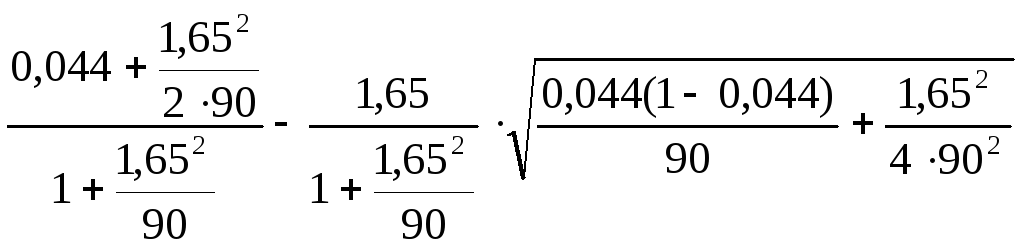=0,020

Р2 = 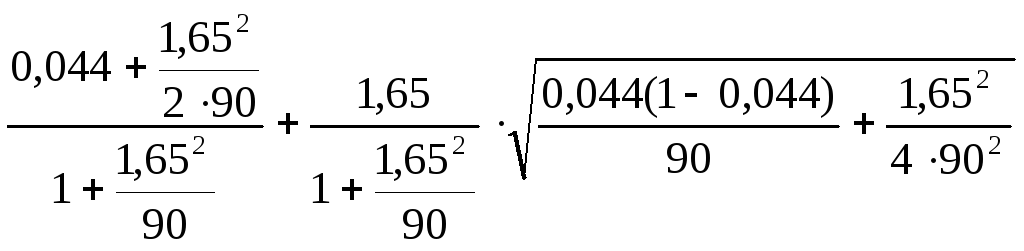=0,095

5. 1) Для построения гистограммы Г(x) заключаем все экспериментальные данные в интервал (0;316) и разбиваем его на 10 равных разрядов.

Значение гистограммы Г(x) находим по формуле : ,

где - число экспериментальных точек, попавших в этот разряд ;

- его длина.

_{величина интервала:}

_{количество разрядов: k =}

величина разряда:

№разряда	Разряд		Частота попадания случайной величины X в разряд		Значение гистограммы Г (х)
	нижняя граница	верхняя граница
			ni
1	-58	-47	2	0,022	0,00200
2	-47	-36	4	0,044	0,00400
3	-36	-25	5	0,056	0,00509
4	-25	-14	7	0,078	0,00709
5	-14	-3	17	0,189	0,01718
6	-3	8	25	0,278	0,02527
7	8	19	12	0,133	0,01209
8	19	30	6	0,067	0,00609
9	30	41	6	0,067	0,00609
10	41	52	6	0,067	0,00609

Гистограмма представлена на рисунке 1.

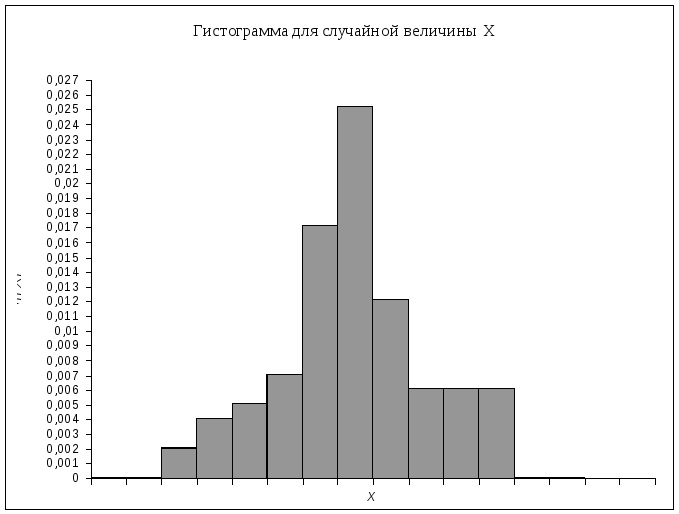
_{Рисунок 1.}