Курсовая работа / Курсовая работа - 2003 / хз

Цель работы:

Работа посвящена наиболее важным методам обработки экспериментальных данных, а именно, оцениванию распределений и их параметров и проверке гипотез о распределениях.

Задание:

В результате испытания контрольной партии, состоящей из 100 тыс. машин, были получены следующие значения времени наработки до первого отказа:

2,1	2,6	3,9	5,6	2,4	0,7	6	0,8	4,2	16,4
12,9	1,8	10,6	11,9	2,2	18,1	12,8	6,6	6,9	1,6
23,8	2,9	0,6	6,3	2,1	0,5	15,9	3,3	11,7	2,6
6,4	0,3	5,8	3,5	2,8	6,2	0,4	7,7	1,6	1,1
8,9	4,8	16,3	13,9	0,7	6,5	9,8	7,6	8,6	3,7
7,1	1,7	1,7	5,7	2	6	23,9	10,9	1,1	0,4
5	1,4	1,6	2,7	3	0,6	4,4	4,9	1,8	20,8
18,5	2,7	2,6	5,4	2,5	0,7	17,7	2,2	6,8	0,6
5,3	0,4	2,1	3,1	6,3	8,9	11,1	12,3	8	3,1
3,1	5,6	2	6,9	2,5	14,7	13,7	2,1	5,2	13

Необходимо:

1. Найти оценки математического ожидания и дисперсии случайной величины Х.

2. Найти доверительные интервалы для математического ожидания и дисперсии, соответствующие заданной доверительной вероятности ( р = 0,95 ).

3. Оценить вероятность попадания случайной величины Х в заданный интервал.

4. Для этой вероятности найти доверительный интервал, соответствующий заданной доверительной вероятности.

5. Построить гистограмму и эмпирическую функцию распределения случайной величины Х.

6. Найти и построить доверительные области для плотности распределения f(x) и функции распределения F(x), соответствующие заданной доверительной вероятности.

Решение:

1.Найдем точечные оценки математического ожидания и дисперсии, учитывая, что n=100.

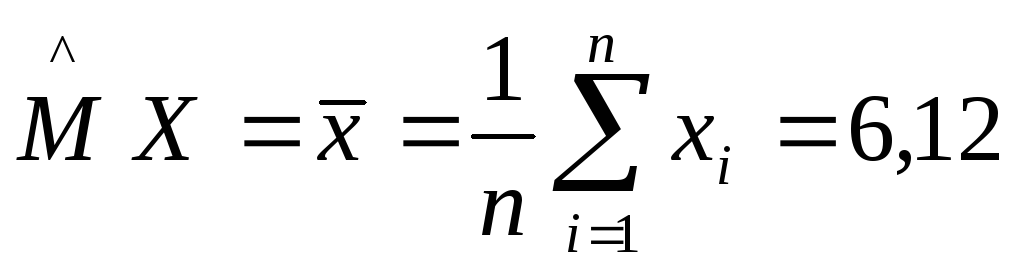
Дисперсия:

Выборочная дисперсия:

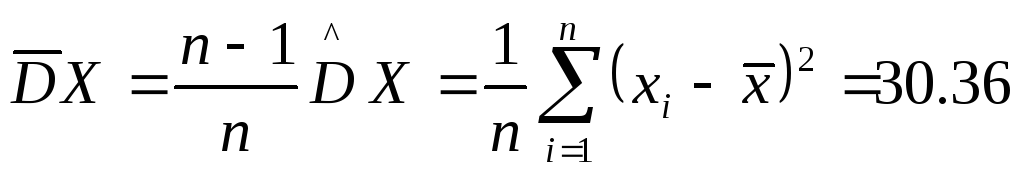
2. Рассчитаем доверительные интервалы для математического ожидания и дисперсии, предварительно задав доверительную вероятность (1-). Пусть (1-) = 0,8. Тогда по таблице значений функции Лапласа находим и,следовательно, искомые доверительные интервалы будут иметь вид:

• для математического ожидания:

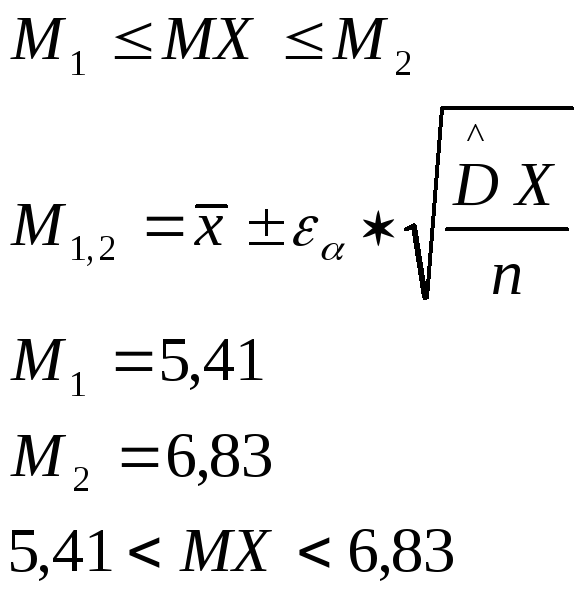
• для дисперсии:

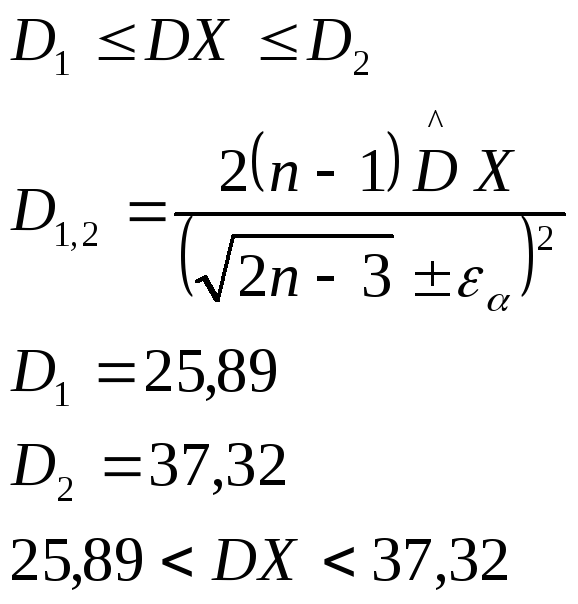
3. Находим точечную оценку вероятности попадания случайной величины X в интервал (0,7;1,1) = (4,28;6,73). Так как в этот интервал попало m=19 экспериментальных значений, то искомая оценка будет равна:

4. Рассчитываем доверительный интервал для вероятности Р, оцененной в предыдущем пункте. Пусть в этом случае доверительная вероятность равна (1-) = 0,95. Тогда =1,96 , и искомый интервал имеет вид :

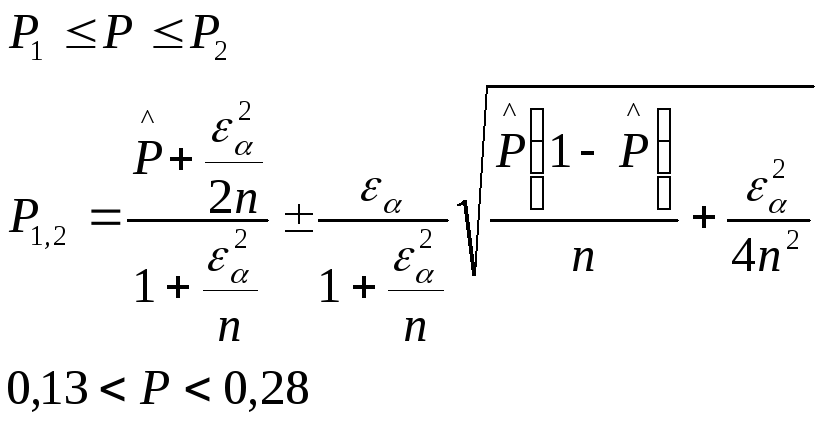
5. Для построения гистограммы Г(x) заключаем все экспериментальные данные в интервал (0; 30) и разбиваем его на 10 равных разрядов, каждый длиной 3. . Для каждого разряда рассчитываем:

• значение гистограммы Г(x):

, где - число экспериментальных точек, попавших в этот разряд , а - его длина.

• частоты попадания экспериментальных точек в разряды гистограммы:

разряды		частота попадания случайной величины X в разряд	значение гистограммы Г(x)
(0;3)	40	0,4	0,133
(3;6)	20	0,2	0,067
(6;9)	18	0,18	0,06
(9;12)	6	0,06	0,02
(12;15)	7	0,07	0,023
(15;18)	4	0,04	0,013
(18;21)	3	0,03	0,01
(21;24)	2	0,02	0,007
(24;27)	0	0	0
(27;30)	0	0	0

Рис.1. Гистограмма.

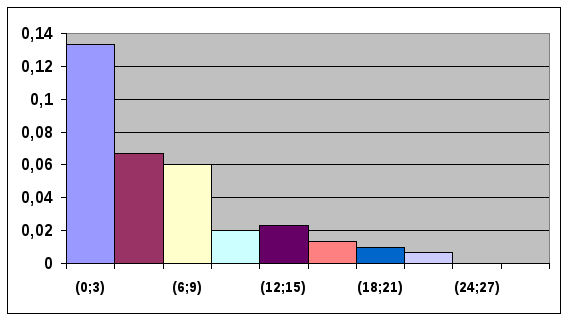
6. Находим доверительные области для плотности распределения f(x) и функции распределения F(x).

На каждом разряде находим доверительную область для вероятности попадания исходной величины X в этот разряд. Вычисляем по формуле (пункт 4.) с заменой величины 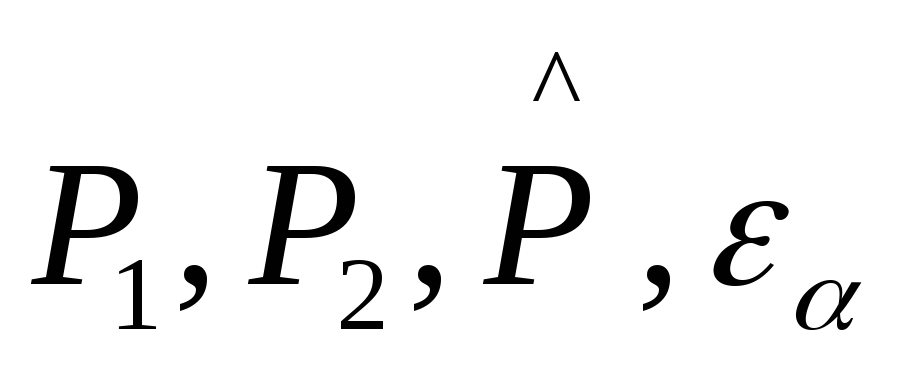соответственно на 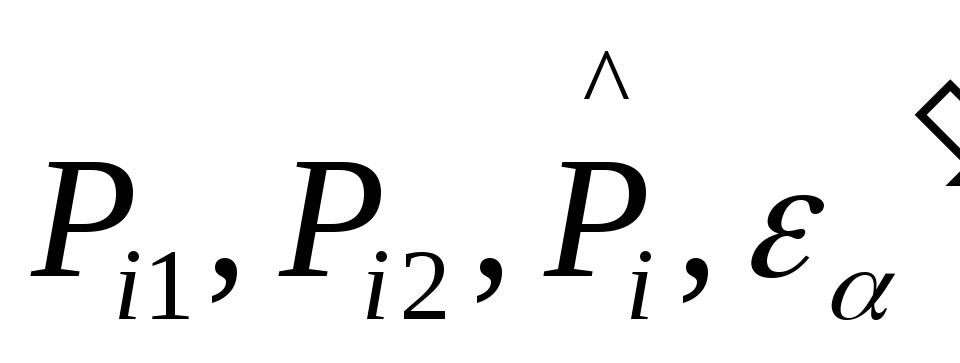. В данном случае общее число разрядов r = 10 плюс 1 полубесконечный разряд , r = 11. Выбираем доверительную вероятность (1-), равную 0,99 , из условия:

и, используя таблицу значений функции Лапласа, находим = 3,36.

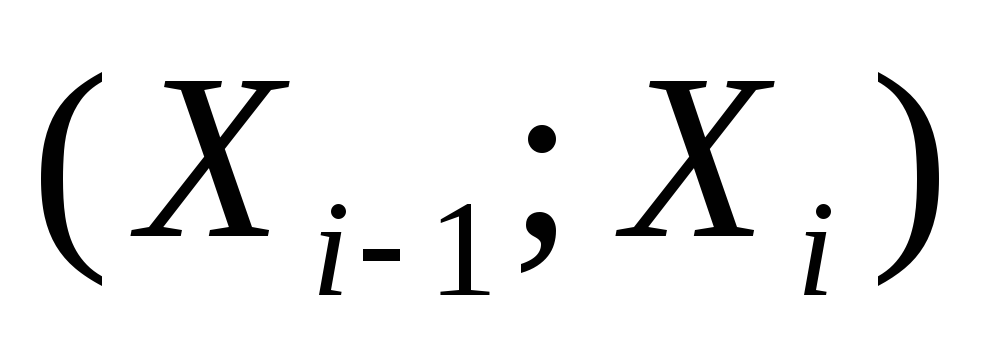
разряд	доверительные границы для плотности распределения f(x)
(0;3)	0,085	0,189
(3;6)	0,033	0,120
(6;9)	0,028	0,113
(9;12)	0,005	0,064
(12;15)	0,007	0,069
(15;18)	0,003	0,055
(18;21)	0,001	0,050
(21;24)	0,000	0,045
(24;27)	0,000	0,000
(27;30)	0,000	0,000

Рис.2. Гистограмма с доверительной областью.

Графической оценкой функции распределения F(x) является эмпирическая функция распределения:

, где - число экспериментальных точек, лежащих левее x.

По таблице распределения величины (распределение Колмагорова) находим ее величину, соответствующую коэффициенту доверия (1-) = 0,99. Она равна =1,6. Затем рассчитываем доверительную область для функции распределения F(x):

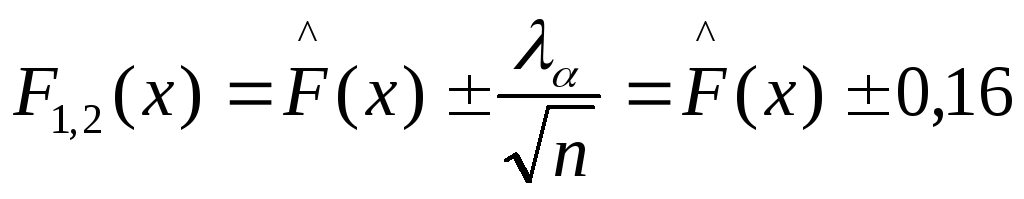
разряд	функция распределения F(x)	доверительные границы для функции распределения F(x)
0	0	0	0,16
3	0,4	0,24	0,56
6	0,6	0,44	0,76
9	0,78	0,62	0,94
12	0,84	0,68	1
15	0,91	0,75	1
18	0,95	0,79	1
21	0,98	0,82	1
24	1	0,84	1
27	1	0,84	1
30	1	0,84	1

Р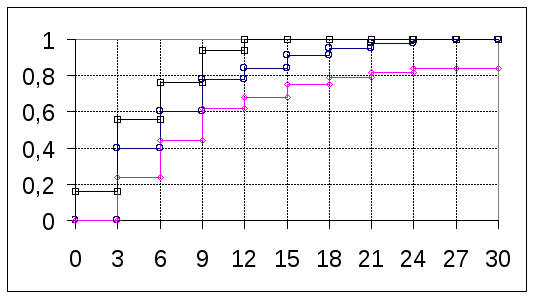 ис.3. График доверительной области функции распределения.

Рис.4. Эмпирическая функция распределения

с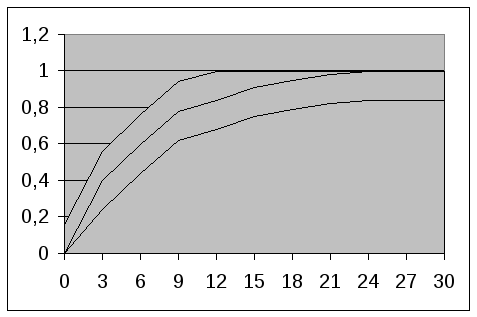 доверительной областью.

7