Информатика / Лабораторные работы / Лабораторная работа 8

ЛАБОРАТОРНАЯ РАБОТА 8.

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ. ЧИСЛЕННЫЕ МЕТОДЫ НАХОЖДЕНИЯ ЛОКАЛЬНЫХ ЭКСТРЕМУМОВ ФУНКЦИИ.

Методические указания

Численные методы решения алгебраических и трансцендентных уравнений. В практике

довольно часто встречаются задачи, приводящие к необходимости решения алгебраических и трансцендентных уравнений. Далеко не все из указанных типов уравнений можно решить аналитически, т.е. получить формулы для вычисления корней. В лабораторной работе рассматриваются некоторые численные методы, позволяющие найти приближенные значения корней уравнений. Точность получаемых решений с практической точки зрения может быть сколь угодно высокой.

Прежде чем перейти к изложению сути методов решения уравнений и способам их реализации в электронной таблице MS Excel, необходимо все же обратить внимание на следующие аспекты:

1.Известно, что уравнение f(x) является алгебраическим, если функция представляет собой алгебраический многочлен порядка n корней, которые могут быть действительными и (или) комплексными. Поскольку в электронной таблице MS Excel не предусмотрено применение арифметики комплексных чисел, мы будем отыскивать лишь действительные корни таких уравнений.

2.Трансцендентные уравнения, в отличие от алгебраических, не позволяют столь однозначно судить о количестве своих действительных корней.

3.Указанные обстоятельства позволяют в дальнейшем специально не оговаривать применимость того или иного метода для решения каждого из типов уравнений.

4.Все численные методы решения уравнений, так или иначе, требуют априорного знания довольно узкого интервала [a, b] на оси х, содержащего корень уравнения. К сожалению, четких рекомендаций по выбору таких интервалов не существует, и в этом случае не последнюю роль играет интуиция и опыт исследователя. Например,

легко показать, что один из действительных корней уравнения х4-8х3-2х2-3х+1=0

находится на интервале [0, 1]. Действительно, простые вычисления показывают, что f(0)=1; f(1)= -11, и поскольку непрерывная функция f(x) имеет противоположные знаки на концах отрезка [0; 1], здесь существует хотя бы один корень.

1. Метод половинного деления (метод дихотомии)

Классическая интерпретация метода половинного деления проста и заключается в следующем.

Пусть известен отрезок [a; b] такой, что f(a)f(b)<0. Это значит, что существует х* [a, b], что f(х*)=0.

Вычислим значение функции f(x) в середине интервала [a, b], т.е. в точке х1=(a+b)/2.

Тогда, х* [a, х1], если f(a)f(x1)<0 или х* [х1, b] f(x1)f(b)<0.

Таким образом, на первом этапе вычислений выделен интервал, содержащий корень, вдвое меньше исходного. Если длина этого интервала соизмерима с требуемой точностью 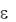определения корня уравнения, вычисления можно прекратить; если же это не так, то процедура деления вновь полученного интервала повторяется. Очевидно, что после N итераций длина интервала, содержащего корень, будет в 2N раз меньше длины отрезка [a; b].

Реализация метода половинного деления в электронной таблице MS Excel в принципе не вызывает особых затруднений.

Вычислительная процедура в Excel может быть реализована так

Вячейки вносим следующие формулы:

Вячейку А2 − а (левая граница интервала локализации корня);

Вячейку В2 − b (правая граница интервала локализации корня);

Вячейку С2 − =(А2+В2)/2;

Вячейку D2 − =f(A2)*f(C2);

Вячейку F2 − 0,001 (абсолютная погрешность);

Вячейку А3 − =ЕСЛИ(D2<=0;A2;C2);

Вячейку B3 − =ЕСЛИ(D2<=0;С2;B2);

Вячейку D3 − =f(A3)*f(C3);

Вячейку Е3 − =ЕСЛИ(ABS(B3-A3)>$F$2;”продолжаем”;”конец”);

После этого выделяются ячейки А3:Е3 и автозаполнением буксируются вниз до появления в столбце Е сообщения “конец”. Вычисленный корень с заданной точностью будет находиться в конце столбца C.

Пример 1. Методом дихотомии вычислить корень уравнения x3-2sinx=0 на отрезке

[1; 2] с точностью 0,001

Заполняем рабочий лист формулами (рис. 1) и с заданной точностью 0,001 определяем значение корня (рис. 2). Ответ находится в ячейке С12 и равен

X= 1,124511719.

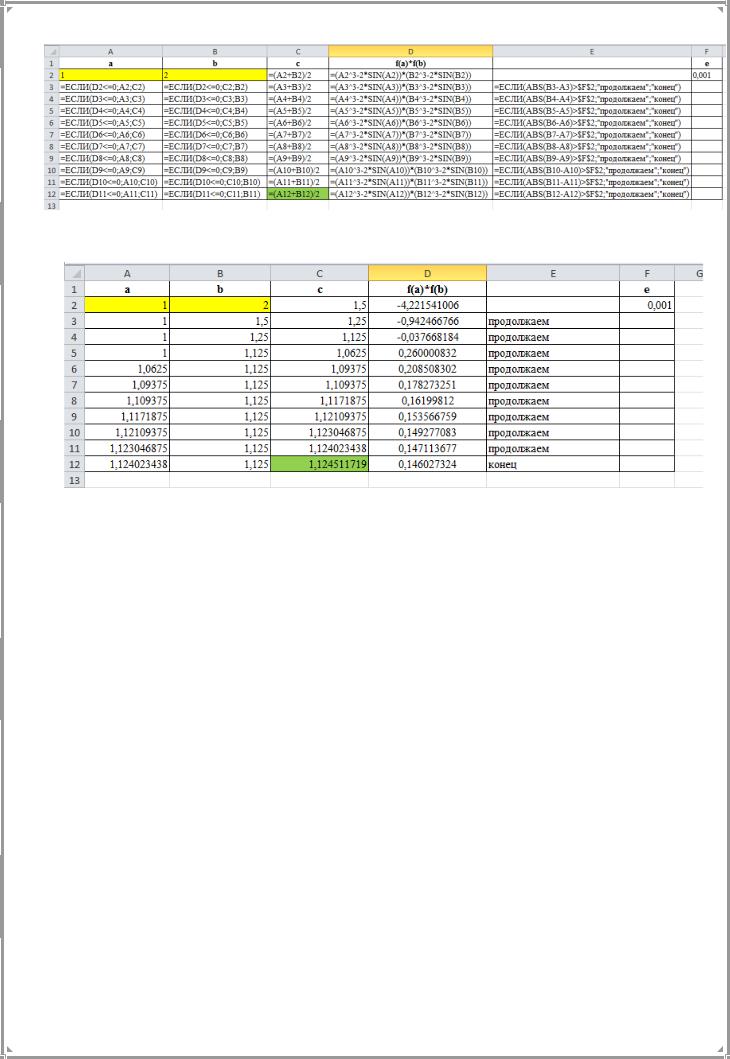
Рис.1. Формулы вычисления корней

Рис. 2. Вычисление корня Х

2. Уточнение корней средством “Подбор параметра”

Обширную группу методов уточнения корня представляют итерационные методы – методы последовательных приближений. Здесь в отличие от метода дихотомии задается не начальный интервал местонахождения корня, а его начальное приближение.

Когда желаемый результат вычислений по формуле известен (подстановка значения корня в уравнение делает его равным нулю), но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра.

При подборе параметра MS Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

Когда задаются условия для применения средства ^ Подбор параметра, в одной ячейке обычно вводится формула, а переменная, которая используется в формуле (с некоторым стартовым значением), задана в другой ячейке.

В формуле можно применять больше одной переменной, но средство ^ Подбор параметра позволяет работать только с одной переменной зараз. Для поиска решения в средстве Подбор параметра применяется итеративный алгоритм. Это означает, что функция сначала проверяет заданное исходное значение параметра и проверяет, дает ли это значение нужный результат. Если исходное значение параметра не дает желаемого результата, средство перебирает другие значения, пока не будет найдено решение.

Поскольку поиск точного решения в некоторых задачах может занять много времени, поэтому MS Excel пытается найти компромисс, устанавливая определенные ограничения по точности решения или максимальному количеству итераций.

Средство Подбор параметра находится на ленте Данные в группе Работа с данными

– Анализ «что если» – Подбор параметра (рис.3).

Рис.3. Основное диалоговое окно средства ^ Подбор параметра

В окне диалога Подбор параметра в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение − ожидаемый результат, в поле Изменяя значение ячейки − ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).

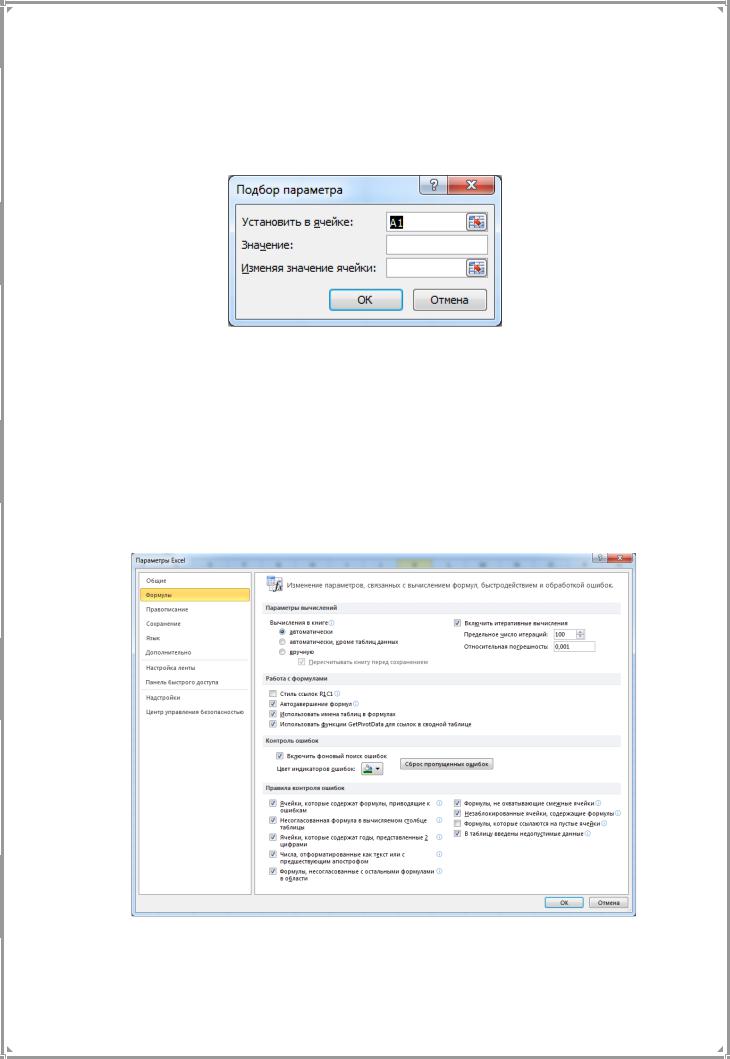
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в Параметрах Excel на странице Форму-

лы. Здесь задается Предельное число итераций (по умолчанию 100) и Относительная погрешность (по умолчанию 0,001) (рис. 4).

Рис. 4 Диалоговое окно Параметры Excel.

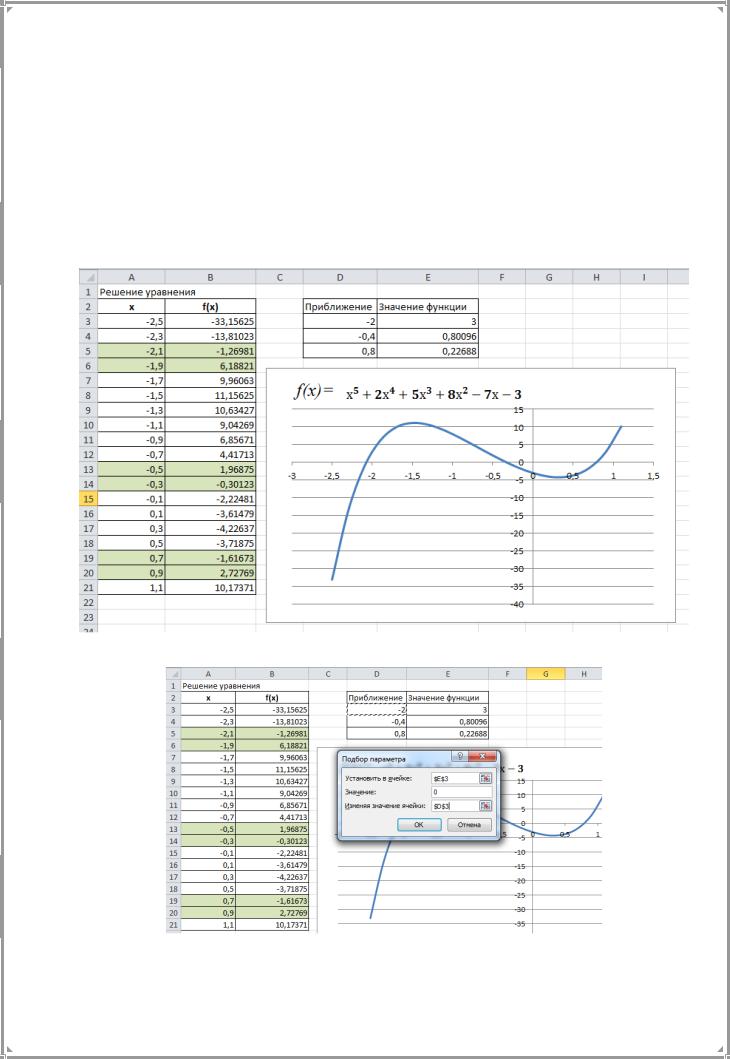
Пример 2. Возьмем в качестве примера уравнение

Для уточнения корней уравнения с помощью средства ^ Подбор параметра локализуем их. В таблице значений функции (в качестве функции рассматривается левая часть уравнения) выявляем интервалы локализации корней уравнения (перемена знака в значении функции): первый интервал ячейки А5:А6, второй интервал ячейки А13:А14, третий интервал ячейки А19:А20 (рис.5).

В каждом интервале выбираем середину и составляем пары ячеек «Приближение» – «Значение функции».

Уточняем значения корней средством ^ Подбор параметра (рис. 6, 7, 8).

Рис. 5.

Рис. 6. Уточнение первого корня уравнения

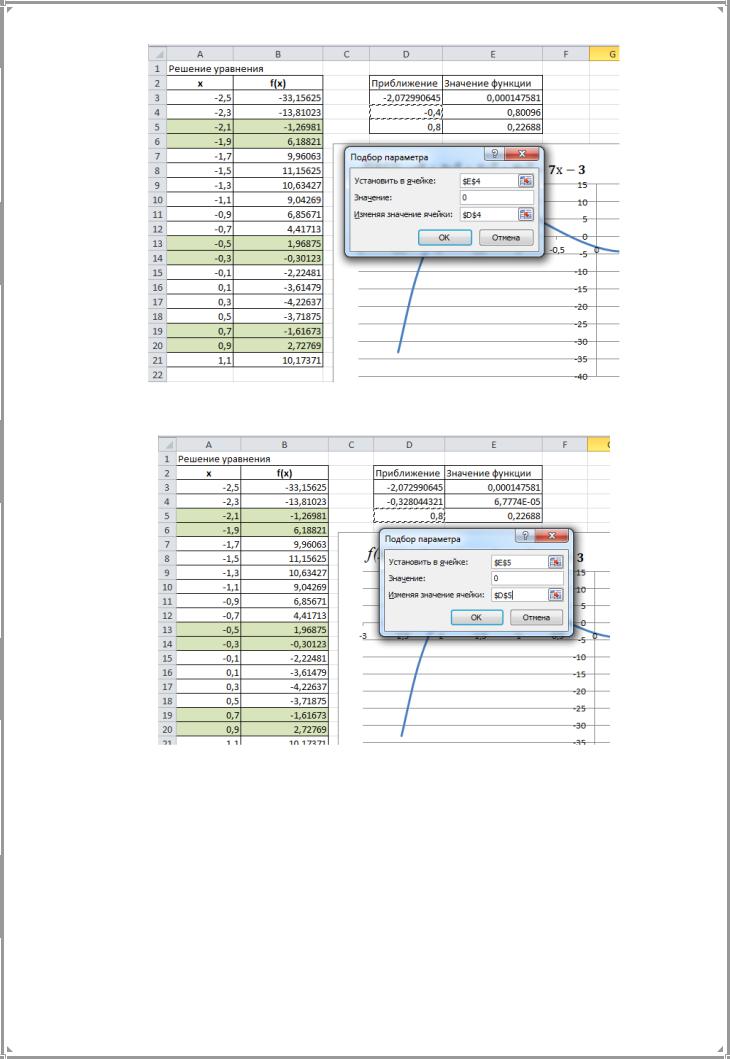
Рис. 7. Уточнение второго корня уравнения

Рис. 8. Уточнение третьего корня уравнения

Ответ: Х1 = -2,07299; Х2 = -0,32804; Х3 = 0,78934.

Численные методы нахождения локальных экстремумов функции. Во многих инженер-

ных задачах интерес представляют не только нули функции (задача нахождения корней уравнения) но и другие важные для практического использования точки. Речь идет об экстремумах функции, т.е. о максимальных и минимальных значениях. Задачи такого рода довольно часто встречаются на практике.

Рассмотрим методы нахождения экстремумов функций одной переменной. Будем рассматривать функцию f(x), непрерывную на [a;b].

Будем считать, что x* a;bявляется точкой минимума функции f(x), если

	f (x* )	f (x)	для всех	x	a;b	(1)
	или точкой максимума, если
	f (x* )	f (x)	для всех	x	a;b	(2)

Задача заключается в том, чтобы найти точку x* и значение f(x*), удовлетворяющее условиям 1 или 2.

В математическом анализе подобная задача решается с использованием аппарата дифференциального исчисления. В этом случае находят все точки подозрительные на экстремум. Некоторые из таких точек определяются из условия равенства нулю первой производной исследуемой функции. Однако на практике применение таких методов довольно ограничено. Поэтому для поиска экстремума функции применяют численные методы. И в этом случае иногда возникают трудности. Это связано прежде всего с априорной неизвестностью характера кривых, являющихся графиками исследуемых функций. Поэтому в общем случае нельзя сказать, сколько экстремумов имеет функция на заданном интервале. Большинство численных методов поиска экстремума не дают ответа на этот вопрос, а найденный с их помощью экстремум может оказаться локальным. Наша задача рассмотреть использование Microsoft Excel как инструмента для решения некоторых типовых задач, ограничимся рассмотрением унимодальных функций, т.е. таких функций, которые имеют единственный экстремум на исследуемом отрезке [a;b].

Решение данной задачи аналогично предыдущей. По графику функции определяются точки экстремумов и вид экстремума (min или max). Для нахождения решения с заданной точностью используют надстройку MS Excel Поиск решения.

Пример 3.

Найти экстремум функции на заданном интервале, с точностью 0,0001:

f (x) cos xe x cos x; x 1,5; 0,5 .

Технология выполнения.

1. Выполните табулирование функции и постройте график.

2.По графику видно, что на заданном интервале функция имеет локальный максимум на отрезке [-0,5; -0,1]. Приближенным значением точки максимума можно взять x равное -0,25, середина отрезка.

3.Для уточнения максимума функции с заданной относительной погрешностью 0,0001 подготовьте таблицу с необходимыми данными.

4.В блок ячеек E3:G4 введите поясняющий текст.

5.Занесите в ячейку E5 приближенное значение точки максимума: -0,25.

6.В ячейку F5 скопируйте формулу из ячейки B3. В ячейку G5 введите тип экстремума “max”.

7. Выполните команду Данные→Поиск решения (в группе команд Анализ). Если в такой команды нет, загрузите надстройку Поиск решения (Параметры MS Excel,

страница Надстройки, кнопка Перейти, включить флажок Поиск решения).

Установить целевую ячейку: введите ссылку на ячейку содержащую функцию (F5), в группе Равной: выберите переключатель максимальному значению, в поле Изменяя ячейки: введите ссылку на ячейку содержащую точку экстремума (E5).

8.Нажмите кнопку Параметры. В диалоговом окне Параметры в поле Относительная погрешность: установите значение 0,0001. Убедитесь, что снят флажок

Линейная модель. Нажмите кнопку OK.

9.В окне Поиск решения нажмите кнопку Выполнить.

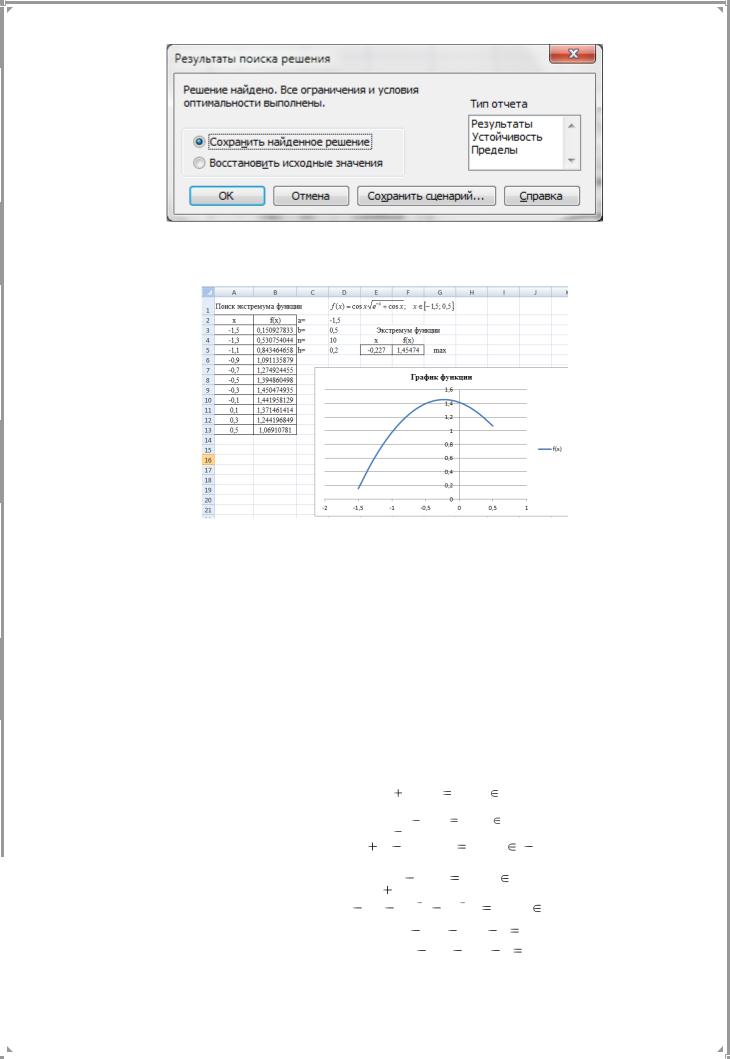
10. В окне диалога Результаты поиска решения нажмите кнопку OK. Если выводиться сообщение об ошибке, то Отмена.

Результат: точка максимума (x max)=-0,22699578467008;

максимум (F max)=1,454739875

ЗАДАНИЕ К ЛАБОРАТОРНОЙ РАБОТЕ

Задание 1.

1.Создать на рабочем диске папку Лаборат_работа 8. Сохранять все созданные книги MS Excel в этой папке.

2.Создать книгу MS Excel, проделать примеры 2 и 3, рассмотренные в методических указаниях лабораторной работы.

3.Найти корни уравнения с точностью 0,0001.

Вариант №

Уравнение

1

sin 5x

cos x2

0,

x

[0,5; 1,5]

2

ln

x

sin x

0,

x [1,5; 3]

x

1

3

2x

4

0,1cos x

0,

x

[ 3; 0]

4

1

sin x

0,

x

[0; 5]

x2

1

5

x2

2x

3(e x xe x )

0,

x [1; 3]

6

x3

3x2

24x

3

0.

7

2x3

3x2

12x 5 0.

4. Найти локальные экстремумы функций с точностью 0,0001.

a)	f (x)	x2 sin xcos x		3x2	x,	x [	1; 0,5];
b) f (x)		0,38x5	1,21x4	1,11x3		0,74x2	3,12x	2,72	x	[	1; 2];
c)	f (x)	2sin x	cos 3x,	x	[1; 3];
d) f (x)		0,68x5	1,14x4	0,56x3		1,84x2	2,15x	1,47	x	[	2,3; 1,3];

	e) f (x)
			sin x			1	x,		x	[1; 3];
	f)	f (x)	1,32x5			0,14x4			0,57x3 1,85x2 2,71x 1,63 x [ 1,3; 1,2];
	g)	f (x)		ln x		x2		x,	x	[0,4;1,4].
				x

Контрольные вопросы

1.Какое уравнение называют алгебраическим?

2.Какое уравнение называют трансцендентным?

3.Назовите критерий того, что на отрезке (а,b) функция f(x) имеет хотя бы один действительный корень.

4.Какое значение корня можно получить при использовании возможностей электронных таблиц для решения уравнений?

5.В каких случаях целесообразно использовать электронные таблицы для решения уравнений?