Пределы_Дифференциальное исчисление

2.3.Если А=0 и В=0, то имеем предел типа 00 - неопределенность. Здесь

могут быть разные случаи.

2.3.1.Если под знаком предела есть синусы, косинусы, тангенсы или обратные им функции, то следует преобразовать выражение под знаком предела так, чтобы можно было применить 1-й замечательный предел. Он тоже имеет такой тип.

2.3.2.Если под знаком предела записано отношение полиномов, то их следует разложить на множители, используя значение корней. Затем до перехода к пределу сократить на множитель, вносящий неопределенность. И далее вернуться к п.1. алгоритма.

2.3.3.Если под знаком предела имеется иррациональность, то перенести ее из числителя в знаменатель (и-или наоборот). Затем обработать полученное по п.2.3.2. и вернуться к п.1.

∞

2.4.Если тип предела ∞ , то преобразуют дробь, используя связь бмв и

ббв(см. частные случаи пределов), и переходят к п.2.3 .

2.5.Если тип предела 0∞, то преобразуют произведение в дробь, используя связь бмв и ббв, и переходят к пунктам 2.3 или 2.4. соответственно.

2.6.Если тип предела ∞-∞, то поступают в зависимости от выражений, дающих ббв.

2.6.1.Если эти выражения – рациональные дроби, то иногда достаточно привести их к общему знаменателю и перейти к п.2.3.

2.6.2. Если эти выражения – разность иррациональностей, то следует перенести ее из числителя в знаменатель и вернуться после упрощения к п.1.

2.7. Пределы типа 1∞ обрабатывают в направлении применения 2-го замечательного предела (сначала выписывают нужную в работе 1; затем оставшиеся слагаемые в основании преобразуют; затем в показателе записывают величину, обратную преобразованному выражению и старый показатель; затем новый показатель умножают на величину так , чтобы сохранилось общее равенство; затем применяют замечательный предел и обрабатывают оставшийся показатель). См. примеры.

2.8. Пределы типа 0о ; ∞о обрабатывают по одной схеме на основании основного логарифмического тождества . Пусть мы имеем предел вида

lim f (x)ф(х) . Тогда выражение под знаком предела следует записать так

х→а

f (x)ф(х) =еф( х) ln f ( x) и затем вычислять предел показателя полученного

выражения. Во всех случаях там получаются пределы, рассмотренные ранее. Пример 3.5. Вычислить пределы.

3.5.1. lim х2 +1 − х . Решение. Это тип предела ∞-∞; он содержит

х→+∞

иррациональности и потому переносим иррациональность в знаменатель, умножив числитель и знаменатель но сопряженное числителю х2 +1 + х .

Получаем lim

( х2

+1 − х)( х2 +1 + х)

=lim

х2

+1− х2

=lim

1

. Получен

х

2

+1

+ х

х

2

+1

+ х

х

2

+

х→+∞

х→+∞

х→+∞

1 + х

предел типа ВА , в которой знаменатель растет, а числитель неизменен. По п.2.2. ответом будет 0.

3.5.2. limх→+∞ 2х2−х 3 3х . Решение. Имеем тип предела 1∞ .Обрабатываем его в направлении 2-го замечательного. Получаем последовательно

	2х	3х			2х	3х			2х− 2х+3	3х
lim			=lim 1	+		−1	=lim 1	+			= (сохранена 1 и
					2х−3				2х−3
х→+∞	2х−3		х→+∞				х→+∞

сделано приведение к общему знаменателю. Предстоит упростить)

				3		2 х−3
		+				3
=lim 1
х→+∞				2х−3
lim	9 x			4,5
=ех→∞ 2x−3 =е

3х

3

2

х−3

2 х−3

=limе

9 х

3

3

=

(т.к. lim 1+

=е)

2 х−3

х→+∞

х→+∞

2х−3

(т.к. lim

9x

=

9

по схеме 2.3.2)

2 x−3

х→∞

2

Примеры эквивалентных бмв.

При достаточно малых х (т.е. х близких к 0) эквивалентными будут:

Sinx	и х ; tgx	и x; arcSinx и x; arctgx и x; ex и 1+x; ln(1+x) и x; 1+ х и 0,5x;
	n 1+ х и	1+	1	x. Эти сведения удобны в приближенных вычислениях и
			n
вычислении пределов.
	1.4.Непрерывность функции в точке и на промежутке.
Опр. Разность		у2-у1= у называют приращением переменной у. Если у=f(x),
то	у= f(x+ х)- f(x).

Опр. f(x) называют непрерывной в точке хо, если беконечно малому приращению аргумента соответствует беконечно малое приращение функции.

Симолически это записывают так lim y .

х→0

Это определение эквивалентно определению : f(x) называют непрерывной в точке хо, если предел функции в этой точке равен значению функции в этой

точке. Симолически это записывают так lim f (x) =f(хо). Часто используют и
	х→xo
такую символику lim f (x) =f(lim x ).
х→xo	х→xo

Из этих определений вытекает, что в точке непрерывности значение функции не бесконечно.

Теорема. Все элементарные функции непрерывны в каждой точке их области определения.

Доказательство проведем на примере одной функции, чтобы показать механизм такой проверки.

Пусть дана функция у=6х2 . Область ее определения – все действительные числа. Возьмем фиксированное х. Вычислим значение функции в этой точке . Имеем f(x)=6х2. Теперь дадим х приращение х и

lim

х→хо х>xo

вычислим	значение	функции		в	новой	точке.	Имеем
f(x+ х)=6(х+	х)2=6(х2+2х х+		х2). Теперь найдем приращение функции при
переходе от одной точки ко второй. Получаем f(x+ х)- f(x)= 6(х2+2х							х+ х2)-
6х2=12х х+	х2 . При	х →0	получаем	lim	y =0. А т.к. точку мы брали
				х→0
произвольно	из области определения, то все				доказанное справедливо в
любой точке области определения. Что и требовалось.
Отметим простейшие свойства функций, непрерывных в точке.

Сумма, разность, произведение и частное конечного числа непрерывных в данной точке функций есть функция непрерывная в этой точке. За исключением случая, когда знаменатель дроби обращается в нуль в этой точке.

Сложная функция (суперпозиция) непрерывна в точке, если непрерывные еe составляющие.

Если у=f(x) непрерывна и монотонна в данной точке, то непрерывна и обратная к ней функция.

Отметим некоторые приемы исследования функций на непрерывность в подозрительной на разрыв точке. Подозрительными на разрыв точками будут точки, где происходит стыковка двух аналитических соотношений, определяющих данную функцию. В этих точках следует проверить выполнение равенства f(хо+0)=f(хо-0)=f(хо) где – хо подозрительная точка, а f(хо+0)= f (x) - правосторонний предел функции в точке; аналогично f(хо-

0) – левосторонний предел. Если равенство нарушается в каком-либо месте, то говорят о разрыве функции в данной точке. При этом разрывы классифицируют: если равенство просто нарушено, но односторонние пределы конечные и функция имеет значение в точке, то разрыв относят к 1- му роду. В противном случае точка считается точкой разрыва 2-го рода.

В заключение сформулируем свойства функций, непрерывных на отрезке.

Опр. Если f(x) непрерывна в каждой точке отрезка, то говорят, что она непрерывна на отрезке.

Теорема. Если f(x) непрерывна на отрезке, то она ограничена на нем. (Т.е. ее значения не бесконечны).

Теорема. Если f(x) непрерывна на отрезке, то она достигает на нем своего наибольшего и наименьшего значений. (Т.е. из всех ее значений можно указать наибольшую нижнюю и наименьшую верхнюю границы)

Теорема. Если f(x) непрерывна на отрезке и принимает на нем значения А и В, то хотя бы в одной точке этого отрезка она принимает любое значение между А и В.

Следствие. Если на концах отрезка функция имеет разные знаки, то внутри отрезка существует хотя бы одно точка, где функция обращается в нуль.

Эту точку называют корнем (нулем) функции. И это свойство используют для изоляции корней конечным отрезком во время приближенного решения уравнений.

2.Дифференциальное исчисление функции одного переменного.

Рассмотрены основные понятия дифференциального исчисления функций одного и нескольких переменных и применение аппарата дифференциального исчисления к решению прикладных задач.

2.1.Определение и осн. свойства производной.

Основным понятием раздела является понятие производной.

Опр. Предел отношения приращения функции в данной точке к вызвавшему его приращению аргумента, когда последнее стремится к нулю, называют производной функции в данной точке.

Если функция задана y=f(x) (т.е. явно), то символически это

записывают так lim	y	=y’. Используют и другие обозначения : f’(x) ; y’(x)
х→0	х

f’x(x) ; y’x(x) и др., о которых будет сказано далее.

Из определения вытекает алгоритм вычисления производной.

1-й шаг. Возьми точку х и вычисли значение функции f(x) в этой точке.

2-й шаг. Возьми приращение аргумента		х, получи новую точку х+ х
и вычисли значение функции f(x+	х) в новой точке.
3-й шаг. Вычисли приращение функции		y = f(x+ х)- f(x), полученное
функцией при переходе от точки х к точке x+		х.
4-й шаг. Найди отношение	у .
	х

5-й шаг. Вычисли, если возможно, предел lim y . Если этот предел

х→0 х

существует, то его значение и есть искомая производная y’ в заданной точке х.

К понятию производной пришли при решении типовых задач физики и геометрии.

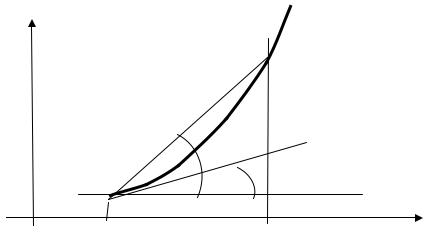
Задача о касательной к кривой. Пусть дана кривая y=f(x). Требуется вычислить угловой коэффициент касательной, проведенной к кривой в заданной точке.

	В
	y=f(x)
β	С
	α
А	D
х	х+ х

Рис 4.1. Геометрическая интерпретация производной

Решение. Возьмем две точки на кривой y=f(x): А(х, f(x)) и В(x+ х,f(x+ х)). Проведем через эти точки секущую АВ. Легко найти угловой коэффициент

	прямой АВ как отношение	f (x + x) − f (x)	=tgβ . Если теперь устремить
		x

х к нулю, то секущая будет поворачиваться и в пределе займет положение касательной АС, угловой коэффициент которой равен tgα=

	lim tgβ=lim	f (x + x) − f (x)	.Все пределы вычислены при условии х →0.
		x

Отсюда следует, что производную функции y=f(x) в данной точке можно истолковать геометрически как угловой коэффициент касательной, проведенной в данной точке к этой кривой.

Задача о скорости. Пусть известен (задан) закон движения s=S(t) (зависимость изменения пути от времени). Найти скорость движения в данный момент времени.

Решение. К моменту времени t пройден путь S(t). Тогда к моменту времени t+ t будет пройден путь S(t+ t ). Это значит, что за время t пройден путь , равный S(t+ t )- S(t). Средняя скорость движения за

	промежуток времени	t можно вычислить по отношению	f (t + t) − f (t)	. Чем
			t

меньше промежуток времени , выбранный для измерения средней скорости, тем точнее средняя скорость характеризует процесс движения. Естественно,

	что при t →0 lim	f (t + t) − f (t)	даст значение скорости движения в момент
		t

времени t – это значение принято называть мгновенной скоростью (или просто скоростью движения в данный момент времени). Поэтому производную S’(t) можно истолковать как скорость движения v(t).

Теорема. Если y=f(x) имеет производную в точке х, то функция

непрерывна в данной точке.		у
Док. Воспользуемся связью предела и	бмв :		=y’+α( х) . Из	этого
		х
соотношения следует непрерывность, т.к.	у= y’	х+α( х) х →0 при		t →0.

Комментарий. Обратное не всегда верно, т.к. предел можно вычислять как односторонний и получать одинаковые ответы. А в самой точке функция может не иметь значения и , значит быть разрывной.

Чтобы всякий раз не применять алгоритм вычисления производной выведем основные правила вычисления производной и составим таблицу производных основных элементарных функций

2.2.Таблица и основные правила.

Применяя алгоритм, легко получить такие правила поиска производных:

(с)’=0 ; x’=1; (u(x) ±v(x))’=( u(x))’ ±(v(x))’.

Сложнее получить формулу (u(x)v(x))’=u’(x)v(x)+u(x)v(x). Получим ее,

несколько сократив запись алгоритма. Получаем f(x)= u(x)v(x). Тогда

f(x+ х)= u(x+	х)v(x+ х). Но лучше это записать так f(x+ х)=
(u(x)+ u )(v(x)+	v ), потому что при изменении переменной х изменяются и

переменные u и v. Далее получаем f(x+

х)- f(x)== (u(x)+

u )(v(x)+

v )--

u(x)v(x)= v(x)

u +u(x) v . Разделим полученное на

х

и вычислим предел

отношения. Получим рабочую формулу.

По аналогичной схеме можно получить производную частного

u(x) '

=

u'(x)v(x) − v'(x)u(x)

.

Для

доказательства

достаточно

записать

v

2

(x)

v(x)

f(x+

u(x + х)

u(x) + u

х)=

в виде f(x+ х)=

и далее продолжить алгоритм

+

v(x

х)

v(x) +

v

u(x) + u u(x)

f (x +

x) − f (x)

=lim

−

=

вычисления производной lim

v(x) +

v

v(x)

x

х

х→0

x→0

v(x) u

u(x) v

u(x)v(x) + v(x) u −u(x)v(x) −u(x) v

−

x

x

lim

=lim

=

(v(x) + v)v(x) x

(v(x) + v)v(x)

x→0

x→0

u'(x)v(x) − v'(x)u(x)

.

v2 (x)

Если y=f(x) и х=ф(у) взаимно обратные функции, то их производные

связаны соотношением y’x=

1

. Доказательство следует из lim

y

=

1

э

х

x

ху

х→0

lim

y

y→0

Если y=f(x) и х=ф(t) (т.е. y=f(ф(t)) – сложная функция), то y’t= y’xx’t ,

где y’x= f’x(x) , а x’t = ф’t(t).

у =

у

x

Доказательство следует из цепочки преобразований

и затем

вычислить предел полученного при

t

х

t

t →0, что приведет к тому что

x →0.

Бывают ситуации, когда функция y=f(x) задана параметрически, т.е. в

виде

x

= x(t)

. Тогда используют тот факт,

что отношение

у

всегда можно

= y(t)

х

y

у

преобразовать по схеме

t

. А при вычислении производной получить в

у

t

ответе запись y’=

у'

t

.

'

xt

Используя эти правила, получаем сначала таблицу производных основных элементарных функций.

Функция

Ее производная

Вывод формулы и комментарии

y=ax , a ≠1,a>0;

y’= ax lna;

Имеем y+

у= ax+ x ,

у=ax+ x -ax = ax (a x -

1)

Теперь lim

a

x

(a

x

−1)

=

a x −1 = z

=

x =

ln(z +1)

х

х→0

ln a

z ln a

= ax lim

= ax lna.

ln(z +1)

y=ex ,

y’= ex ;

z→0

Как частный случай для предыдущей

1

формулы.

y=lnx

y’=

;

Т.к. х=eу , то на основании связи производных

х

взаимно обратных функций имеем

(lnx)’x= (e1y)'y y=хα ,

y=Sinx

y=Cosx

y=tgx

y=arcSinx

(arcSinx)’=

11

==ey = х .

y’=αхα−1 ,

y’=Cosx

y’=-Sinx

1 y’= cos2 x

y’=	1
	1− х2

Имеем y=хα = eαlnx . Далее используем предыдущую формулу и производную от сложной

функции y’= e

αlnx α 1

= αх

α−1

.

х

2х+

х

х

Имеем

у=Sin(x+

х)-Sinx=2Cos

Sin

;

2

2

теперь y’= lim

2Cos0,5(2x + x)Sin(0,5

x)

=

x→0

x

lim

Sin(0,5 x)

Cos0,5(2x +

x) =Cosx.

x→0

0,5 x

В самом деле (Cosx)’=(sin( π2 -x))’=

Cos( π2 -x)(-x)’=-Sinx. Применена формула

Приведения и производная сложной функции.

Достаточно записать производную от дроби

			Sinx '			далее преобразовать рез-т.
	(tgx)’= Cosx
	В самом деле, по условию x=Siny. Для
	взаимно			обратных				функций имеем
	=	1	=	1		=	1	=	1	.
		(Siny)'		Cosy			+ Sin2 y		+ x2
						1		1

y=arctgx	y’=			1						Схему получения смотри выше.
		1	+ x				2
										Ввиду того, что arcCosx= π -arcSinx.
y=arcCosx	y’=-					1
				1− х2						2
y=arcctgx	y’=-						1			Схему получения смотри выше.
				1		+ x			2

В тех случаях, когда применить вышеприведенные правила и таблицу затруднительно, можно использовать прием, называемый логарифмическим

дифференцированием . Пусть мы имеем y= f (x)ф( х) . Тогда невозможно

применить ни одну их записанных выше формул. Поступают так. Сначала логарифмируем обе части равенства и получаем lny=ф(х)ln(f(x)). Теперь возьмем производную от каждой части равенства, зная, что у – это функция

от х. Получаем

1

y’=ф’(x)lnf(x)+ф(x)

1

f’(x).

Из полученного равенства

f (x)

у

найдем требуемое

1

1

y’=y(ф’(x)ln(f(x))+ф(x)

f’(x))=

f (x)ф( х) (ф’(x)ln(f(x))+ф(x)

f’(x)).

f (x)

f (x)

Возможен и другой подход. Имеем y= f (x)ф( х) =eф( x) ln( f ( x)) . После чего

можно искать производную по правилу сложной функции. Получаем

y’=eф( x) ln( f ( x)) ( ф’(x)lnf(x)+ф(x)

1

f’(x))=

f (x)ф( х)

(ф’(x)ln(f(x))+ф(x)

f

(x)

1

f’(x)).

f (x)

Если же функция y=f(x) задана неявно, т.е. уравнением F(x;y)=0, то для

поиска производной следует взять производную от равенства F(x;y)=0, зная, что у= f(x), хотя f(x) и неизвестна. Затем из полученного равенства находят y’.

2.3.Производная и дифференциал.

Из связи предела и бмв для производной получаем y =f’(x) x +α x , где α - бмв. Т.к. слагаемые в сумме , записанной справа неравноценны по

величине (произведение α x имеет порядок малости более высокий, чем		x ,
а первое слагаемое имеет порядок малости,	такой же как и x ), то одно из
них выделим в виде определения.	x часть приращения функции
Опр. Главная, линейная относительно
называется дифференциалом функции и обозначается dy.
Получаем dy= f’(x) x . Иногда используют обозначение df(x)= f’(x)		x .
Т.к. x =dx, то обозначение дифференциала принимает симметричный вид
dy= f’(x)dx или df(x)= f’(x)dx или dy=y’dx.

Используя новое понятие, можно сказать что производная есть отношение дифференциалов функции и аргумента. Этот факт дает новые

формы

записи

для

символа

производной

:

y’=f’(x)=y’(x)=

dy

=

df (x)

=

d

y =

d

f .

dx

dx

dx

dx

Можно достаточно просто истолковать дифференциал – это приращение касательной к кривой в данной точке. (cм. Рис 4.1. DB – это приращение у функции y=f(x); DC – приращение dy касательной плоскости

. Простейшие свойства дифференциала вытекают из соответствующих свойств производной (аддитивности, однородности и линейности)

С помощью дифференциала можно получить известную формулу для вычисления производной параметрически заданной функции. Имеем

	x = x(t)		dу		у't dt
		. Тогда отношение y’= dх		принимает вид y’= х't dt		и затем получить
	y = y(t)

у' y’= t' .

xt

Используем дифференциал для приближенных вычислений ввиду того, что у, которое мы не знаем во многих случаях, можно приближенно заменить на величину dy, которое всегда можно вычислить. Это положено в основу приближенной формулы f(x+ x )=f(x)+ у=f(x)+f’(x) x . Пусть нам требуется вычислить значение функции у= f(x) , но точно сделать это затруднительно. Тогда можно предложить алгоритм применения дифференциала:

-выбери точку хо достаточно близко к точке х и вычисли значение f(xо);

-вычисли значение f’(xо) и значение	x =х- хо ;
-вычисли приближенно f(x) , заменив	у на f’(xо) x .

Пример 4.1. Вычислите приближенно ln1,2. Решение. Выбираем подходящую по записи функцию f(x)=lnx. Нам предстоит вычислить ее значение при х=1,2. Сделать это мы не можем. Выберем хо=1. Найдем

	dy= f’(xо) x при x =1,2-1=0,2. Получаем (lnx)'=	1	=1 при хо=1. Теперь
		х

вычислим приближенное значение ln1,2=ln1+1*0,2=0,2. О погрешности результата в данный момент речи не идет – нужно хотя бы приближенное значение.

Дифференциал обладает свойством инвариантности (неизменность формы записи в зависимости от вида задания функции).

Пусть у= f(x) и х=ф(t). Тогда dy=f’tdt. Но dx=ф’tdt. C другой стороны мы знаем, что f’t=f’хф’t . Поэтому dy=f’tdt= f’хф’tdt=f’х dx – т.е.

форма записи сохранилась.

2.4.Производная и дифференциал высшего порядка.

Т.к. y’ сама является функцией, то естественно поставить вопрос о наличии ее производной, т.е. (y’)’. Все это можно обобщить определением: производная от производной порядка n-1 называется производной порядка n.

Соответственно записывают символ такой производной y(n)=(y(n-1))’. Если использовать для обозначения символ дифференциала, то получим иные

	(n)		d n y			d n f (x)			d n
обозначения производной порядка n. y		=			=			=			f (x) и т.д. В
			dx	n		dx	n		dx	n

самом деле по определению имеем y’’=(y’)’=(f’(x)dx)’=(f’’(x)dx)dx=f’’(x)d2x.

Откуда и получаем в виде обобщения записанное ранее.

Из этого определения вытекают и все свойства такой производной. Рассмотрим несколько частных случаев производной порядка n.

Пусть y=uv. Тогда y’=u’v+v’u. Затем y’’=u’’v+2u’v’+v’’u. Обобщаем и получаем

(uv)(n) =u(n) v+n u(n-1)

v’+

n(n −1)

u(n−2) v'' +…+ uv(n)

. коэффициенты такой

2 !

формулы можно сразу выписать, если использовать треугольник Паскаля.

= x(t)

x

Пусть функция задана параметрически

y = y(t) .

Тогда известно, что

у'

y’=

t

. Если теперь

попытаться

найти

y’’,

то

сделать

это будет

'

xt

проблематично, т.к. получено выражение,

зависящее от

t

,но не от х.

Обойдем это затруднение так – имеем

у

'

у' '

у' '

t

t

t

d

d

у'

d x

'

xt' dt

xt' dt

у''

t

x'

−x''

t

y'

t

y’’=(y’)’=

y’=

(

t

)=

t

=

=

=

t

.

dx

dx

'

dx

dx

x'dt

'

)

3

xt

(xt

Можно поступить иначе

d

d

у'

d

dF(t)

F

'

(t)

y’’=(y’)’=

y’=

(

t

)=

( F(t) )=

=

t

.

dx

dx

xt

dx

dx

x't

2.5.Теоремы о среднем.

В этот раздел включен ряд теорем, имеющих важное теоретическое значение и являющихся базовыми при построении многих вычислительных схем.

Теорема Ролля. Если f(x) непрерывна на [a;b], дифференцируема внутри его ( т.е. на (a;b) ), а также имеет место равенство f(a)=f(b), то

с (a;b) такая, что f’(c)=0.

Комментарий. Геометрически это означает, что внутри отрезка есть по крайней мере одно точка, в которой касательная к кривой параллельна Ох.

Док. Т.к. f(x) - непрерывна, то существуют на этом отрезке наибольшее М и наименьшее m значения этой функции.

1.Пусть М= m. Это означает, что f(x)=сonst и потому f’(х)=0 (в любой точке).

2.Пусть M>m. Тогда из условия f(a)=f(b) следует, что либо М, либо m находятся внутри отрезка [a;b]. Пусть это будет М. Тогда возьмем в качестве