Pobegailo

a1x + a2 y + a3z +a = 0,

где

y1

z1

1

x1

z1

1

a1 =

y2

z2 1

, a2 = −

x2

z2

1

,

y3

z3 1

x3

z3

1

x1

y1

1

x1

y1

z1

a3 =

x2

y2

1

, a = −

x2

y2

z2

.

x3

y3

1

x3

y3

z3

Приведем это уравнение секущей плоскости к нормальномувиду, получим n1x + n2 y + n3z − d = 0,

где

ni =			ai
		a2	+a2	+ a2
	1		2	3
для i {1, 2, 3} и
d = −			a			.
		a2	+a2	+a2
	1		2	3

Такая секущая плоскость, как было показано в разделе 5.3, пересекает

сферу S 2 по малой окружности сферы.

Определим центр этой малой окружности. Для этой цели определим ось

n1 n = n2 ,n3

которая перпендикулярна секущей плоскости. Обозначим через c радиус-

вектор точки C, которая является центром сферы S 2. Тогда, принимая во внимание, что начало системы координат совпадает с центром сферы

S2 , радиус-вектор c определяется следующим образом: c = dn,

так как значение d равно расстоянию от секущей плоскости до начала системы координат.

170

Определим ось n и центр окружности c, используя векторные операции. Для этой цели введем вектор

a1 a = a2 .

a3

Тогда

	n =	a		,	d = −	a	.
		| a	|			| a |

Теперь предположим, что точки P1, P2 и P3 описываются соответственно радиус-векторами p1, p2 и p3 относительно выбранной системы координат. Тогда из равенств для вычисления значений скаляров a1, a2 , a3 и a получим, что

a = ( p3 − p2 ) ×( p1 − p2 ), a = −[ p1 p2 p3],

где

[ p1 p2 p3] = ( p1 × p2 ) p3 = p1 ( p2 × p3)

обозначает смешанное векторное произведение. Следовательно, используя векторные операции, ось n и центр c могут быть определены следующим образом:

n =		( p3 − p2 ) ×( p1 − p2 )									,
		| ( p	− p			) ×( p		− p	) |
		3		2		1		2
c =			[ p1 p2 p3]							n.
	| ( p		− p		) ×( p		− p		) |
		3	2			1		2

(8.1)

(8.2)

Определим дугу малой окружности от точки P1 до точки P3 , которая проходит через промежуточную точку P2 . Для этой цели нужно определить центральные углы

ϕ = PCP ,		ψ = P CP .
1	2	2	3

Для краткости аналитических выражений введем следующие обозначения для радиус-векторов:

r1 = p1 −c, r2 = p2 −c, r3 = p3 −c, n1 = r1 ×r2 , n2 = r2 ×r3,

171

и скаляров:

n1 =| n1 |,	n2 =| n2 |,
s1 = r1 r2,	s2 = r2 r3.

Используя эти обозначения, центральные углы ϕ и ψ могут быть определены следующим образом:

arctan 2(n1, s1),			n1 n > 0,
ϕ = 2π−arctan 2(n ,s ),			n n < 0,	(8.3)
	1	1	1
arctan 2(n2 ,s2 ),			n2 n > 0,
ψ = 2π−arctan 2(n , s ),			n n < 0.	(8.4)
	2	2	2

Тогда требуемая дуга малой окружности может быть описана следующей параметризованной кривой:

p(u) = R(n,u(ϕ+ψ)) p1

для u [0, 1].

На рис. 8.1 показана дуга малой окружности сферы, построенная по трем точкам на поверхности сферы, используя приведенные формулы.

Рис. 8.1. Дуга малой окружности сферы, построенная по трем точкам

8.3. Деформация дуг окружностей

Рассмотрим сферу S2 , которая описана каноническим уравнением

x2 + y2 + z2 = r2

172

относительно ортогональной системы координат с началом в центре сферы. Возьмем две произвольные различные точки P1 и P2, лежащие на

поверхности сферы S 2. Предположим, что точки P1 и P2 описываются соответственно радиус-векторами p1 и p2 относительно выбранной системы координат. Рассмотрим две произвольные окружности

p(u) = R(m,uϕ) p1, q(u) = R(n,uψ) p1

для u [0, 1], которые лежат на поверхности сферы S 2 щие граничные точки:

p(0) = q(0) = p1, p(1) = q(1) = p2.

(8.5)

(8.6)

и имеют следую-

(8.7)

Из этих уравнений видно, что дуги окружностей p(u) и q(u) соединяют

точки P1 и P2.

Проблема заключается в следующем. Нужно построить такую параметризованную кривую r(u), которая лежит на поверхности сферы S 2 и удовлетворяет следующим граничным условиям:

r(0) = p1,	r(1) = p2,	(8.8)
r(k ) (0) = p(k ) (0),	r(k ) (1) = q(k ) (1)	(8.9)

для всех k {1, 2, ..., n}, где n N. Параметризованную кривую r(u) бу-

дем называть деформацией параметризованной кривой p(u) в парамет-

ризованную кривую q(u).

Используя сглаживающие полиномы wn (u), рассмотренные в разделе 7.5, определим параметризованную кривую r(u) следующим образом:

r(u) = R(n, wn (u)uψ)R(m,(1− wn (u))uϕ) p1

(8.10)

для u [0, 1]. Отметим, что данная кривая лежит на поверхности сферы

S2 , так как является орбитой ортогонального поворота. В следующих теоремах покажем, что эта параметризованная кривая удовлетворяет требуемым граничным условиям и инвариантна относительно перехода между ортогональными системами координат.

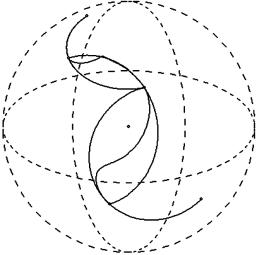
Пример деформации дуг окружностей сферы показан на рис. 8.2.

173

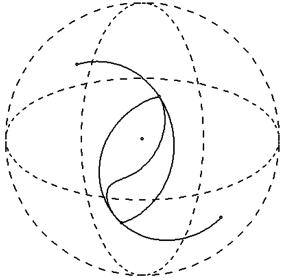
Рис. 8.2. Деформация дуг окружностей на сфере

Теорема 1. Параметризованная кривая r(u), заданная формулой (8.10),

удовлетворяет граничным условиям, заданным равенствами (8.8) и (8.9). Доказательство. Принимая во внимание равенства (8.5), (8.6) и (8.7),

из определения параметризованной кривой r(u) следует, что

r(0) = R(n,0)R(m,0) p1 = p1,

r(1) = R(n,ψ)R(m,0) p1 = R(n,ψ) p1 = p2.

Следовательно, граничные условия, заданные равенствами (8.8), выполняются. Кроме того, из теоремы, доказанной в разделе 7.7, следует, что

(R(n, w (u)uψ)R(m,(1− w (u))uϕ))(k ) (0) = R(k ) (m,uϕ))(0),
n	n
(R(n, w (u)uψ)R(m,(1− w (u))uϕ))(k ) (1) = R(k ) (n,uψ))(1)
n	n
для всех k {1, 2, ..., n}, где n N. Следовательно,
r(k ) (0) = (R(n, w (u)uψ)R(m,(1− w (u))uϕ))(k ) (0) p =
n	k	1
= (R(m,uϕ))(k ) (0) p = p(k )		(0)
	1

и аналогично

r(k ) (1) = (R(n, wn (u)uψ)R(m,(1− wk (u))uϕ))(k ) (1) p1 = = (R(n,uψ))(k ) (1) p1 = q(k ) (1)

для всех k {1, 2, ...,n}, где n N. Таким образом, граничные условия,

заданные равенствами (8.9), также выполняются. Теорема доказана.

174

Теорема 2. Параметризованная кривая r(u), заданная формулой (8.10), инвариантна относительно перехода между ортогональными системами

координат с началом в центре сферы S 2.

Доказательство. Возьмем произвольную ортогональную систему

координат с началом в центре сферы S 2. Обозначим через R ортогональную матрицу перехода к новой ортогональной системе координат с началом в центре сферы. Для краткости введем следующие обозначения:

R−(u) = R(m,(1− wk (u))uϕ), R+(u) = R(n, wk (u)uψ).

Тогда координаты радиус-вектора p1 и параметризованных ортогональ-

ных поворотов R−(u), R+(u) преобразуются при переходе к новой системе координат следующим образом:

p1 = R−1 p1,

R−(u) = R−1R−(u)R, R+(u) = R−1R+(u)R.

Используя эти равенства, координатное представление сферической кривой r(u), описанной формулой (8.10), преобразуется при переходе к но-

вой системе координат как

R−1r(u) = R−1R+(u)R−(u) p1 =

= R−1R+(u)RR−1R−(u)RR−1 p1 = R+(u)R−(u) p1 = r(u).

Отсюда следует, что координатное представление сферической кривой r(u) относительно новой системы координат может быть получено из

исходного представления этой кривой r(u) посредством поворота, за-

данного матрицей R−1. Теорема доказана.

8.4. Построение сплайн-кривой на сфере

Теперь приведем детальное описание алгоритма построения интерполирующей кривой r(t) Cn на поверхности сферы S2 , которая проходит через последовательность точек (P1, P2 , ..., Pk ). Для этой цели введем следующие обозначения:

• сегменты интерполирующей кривой r(t) будем обозначать ri (t) для всех i {1, 2, ..., k −1}. При этом предполагается, что сегмент ri (t) соединяет точки Pi и Pi+1;

175

• нормаль к секущей плоскости, которая определяется тремя последовательными точками Pi , Pi+1 и Pi+2 , будет обозначаться как ni ;

• центр окружности, которая определена тремя последовательными точками Pi , Pi+1 и Pi+2 , будет обозначаться как Ci ;

•центральные углы этих окружностей будут обозначаться как

ϕi = PiCi Pi+1, ψi = Pi+1Ci Pi+2;

•через pi обозначим радиус-векторы соответствующих точек последовательности Pi для всех i {1, 2, ..., k}.

Тогда сформулированная в разделе 8.1 проблема построения интерполирующей сплайн-кривой может быть решена по следующемуалгоритму.

Шаг 1. Выполним следующие вычисления:

1.Определим ось n1, используя формулу (8.1).

2.Определимцентральныеуглы ϕ1 и ψ1, используяформулы(8.3) и(8.4).

3.Сгенерируем первый сегмент интерполирующей сплайн-кривой r(t), используя следующую формулу:

r1(t) = R(n1,u(t)ϕ1) p1,

(8.11)

где

u(t) = t −t1 t2 −t1

для t [t1, t2 ].

Здесь узлы t1 и t2 выбираются, принимая во внимание некоторые ки-

нематические требования или ограничения.

Очевидно, что параметризованная кривая r1(t) имеет следующие граничные точки:

r1(t1) = R(n1,u(t1)ϕ1) p1 = R(n1,0) p1 = p1, r1(t2 ) = R(n1,u(t2 )ϕ1) p1 = R(n1,ϕ1) p1 = p2.

Шаг i для каждого i {2, 3, ..., k − 2}. Выполним следующие вычисления:

1.Определим ось ni , используя формулу (8.1).

2.Определимцентральныеуглы ϕi и ψi , используяформулы(8.3) и(8.4).

3.Сгенерируем сегмент ri (t) интерполирующей кривой r(t), используя формулу (8.10):

ri (t) = R(ni ,wn (u(t))u(t)ϕi )R(ni−1,(1− wn (u(t)))u(t)ψi−1) pi , (8.12)

176

где

u(t) =	t −ti
	t	−t
	i+1	i

для t [ti ,ti+1].

Здесь wn (u) обозначают сглаживающие полиномы, которые были оп-

ределены в разделе 7.5. Значение индекса n сглаживающих полиномов должно совпадать с требуемой степенью непрерывности интерполирующей кривой r(t). Для того чтобы обеспечить параметрическую непре-

рывность интерполирующей кривой r(t)			в узловых точках Pi для всех
i {2, 3, ..., k −1}, узлы ti определяются следующим образом:
t	= t +	(ti −ti−1)	ψ	i−1
i+1	i	ϕi−1

для всех i {2, 3, ..., k −1}.

Очевидно, что параметризованная кривая ri (t) имеет следующие граничные точки:

r(ti ) = R(ni , wn (u(ti ))u(ti )ϕi )R(ni−1,(1− wn (u(ti )))u(ti )ψi−1) pi = = R(ni ,0)R(ni−1,0) pi = pi ,

r(ti+1) = R(ni , wn (u(ti+1))u(ti+1)ϕi )R(ni−1,(1− wn (u(ti+1)))u(ti+1)ψi−1) pi = = R(ni ,ϕi )R(ni−1,0) pi = pi+1

для всех i {2, 3, ..., k −1}.

Шаг (k −1). Генерируем последний сегмент интерполирующей кривой r(t), используя следующую формулу:

rk−1(t) = R(nk−2 ,u(t)ψk−2 ) pk−1,

(8.13)

где

u(t) = t −tk−1 tk −tk−1

для всех t [tk−1, tk ].

Для того чтобы обеспечить параметрическую непрерывность интерполяционной кривой p(t) в узловой точке Pk , значение узла tk опреде-

ляется по следующей формуле:

tk = tk−1 + (tk−ϕ1 −tk−2 ) ψk−2. k−2

177

Очевидно, что параметризованная кривая rk−1(t) имеет следующие граничные точки:

rk−1(tk−1) = R(nk−2,u(tk−1)ψk−2 ) pk−1 = R(nk−2 ,0) pk−1 = pk−1, rk−1(tk ) = R(nk−2 ,u(tk )ψk−2 ) pk−1 = R(nk−2 ,ψk−2 ) pk−1 = pk .

Тогда параметризованная кривая r(t) определяется как последовательность сегментов ri (t), т. е.

r(t) = ri (t)

для t [ti , ti+1], где i {1, 2, ..., k −1}. Очевидно, что определенная таким образом параметризованная кривая r(t), имеет следующие свойства:

1.Проходит через узловые точки Pi для всех i {1, 2, ..., k}. Таким образом, r(t) является требуемой интерполирующей кривой.

2.Из теоремы 1, доказанной в разделе 8.3, следует, что параметризованная кривая r(t) имеет n-ю степень непрерывности, т. е. r(t) Cn.

3.Кроме того, из теоремы 2, доказанной в разделе 8.3, следует, что параметризованная кривая r(t) инвариантна относительно перехода между

ортонормированными системами координат с началом вцентре сферы S 2. Следовательно, параметризованная кривая r(t) удовлетворяет всем

сформулированным в разделе 8.1 требованиям.

Пример построения сплайн-кривой на сфере, используя предложенный подход, показан на рис. 8.3.

Рис. 8.3. Сплайн-кривая на сфере

178

8.5. Постановка задачи сглаживания ломаной линии на сфере

Рассмотрим сферу S2 , которая описана каноническим уравнением

x2 + y2 + z2 = r2

относительно ортогональной системы координат, центр которой находит-

ся в центре сферы. Пусть на поверхности сферы S 2 заданы три различные точки P1, P2 и P3. Предположим, что точки P1 и P2, а также точки P2 и P3

соединены дугами больших окружностей. В общем случае эти дуги больших окружностей образуют угол в точке P2. Выберем некоторые точки Q1

и Q2 , которые лежат на этих дугах больших окружностей и отмечают соответственно начало и окончание сглаживания угла в точке P2.

Задача формулируется следующим образом:

1. Нужно построить параметризованную кривую r(t), которая состоит

из трех сегментов. Первый сегмент этой кривой описывает дугу большой окружности от точки P1 до точки Q1. Второй сегмент этой кривой сгла-

живает угол в точке P2. Третий сегмент этой кривой описывает дугу большой окружности от точки Q2 до точки P3.

2. Параметризованная кривая r(t) должна принадлежать классу Cn ,

т. е. иметь непрерывные производные до порядка n включительно.

3. Дополнительным требованием к параметризованной кривой r(t)

является ее инвариантность относительно выбора ортогональной системы координат с началом в центре сферы.

Параметризованную кривую r(t) будем называть сплайн-кривой на

поверхности сферы S2 , которая сглаживает угол в точке P2.

Предлагаемое решение этой проблемы, которое рассматривается в дальнейших разделах, базируется на сглаживании дуг больших окружностей сферы, которые соединяют точку Q1 с точкой P2 и точку P2 с точ-

кой Q2.

Здесь следует заметить, что выбор точек Q1 и Q2 зависит от различ-

ных кинематических или геометрических требований к сглаживающей сплайн-кривой r(t). Например, при трассировке кривой роботом-манипу-

лятором точки Q1 и Q2 могут быть выбраны настолько близко к точке P2, насколько позволяют кинематические и динамические характеристики робота-манипулятора.

179