1* Задачи, приводящие к понятию двойного интеграла.

Вычисление объёма цил. тела приводит нас к понятию ДИ Цилиндр телом называют тело, где пространство тела ограниченно цилиндр. пов-ю., плоскостью перпендик. образующей ц.т. и поверхностью, пересекающ. цил.пов-ть и не пересекающ. указанную плоскость.

Vпрям.цил.=S*h

Vц.т. = _i=1∑ⁿf(x_i, y_i)∆v_i точность рав-ва будет зависеть от размеров столбиков

Объём цил. Vц.т. = lim_{d→0 i=1}∑ⁿf(x_i, y_i)∆v_i

2* Определение, теоремы существования двойного интеграла. Свойства двойного интеграла

Если ф-ция f(x,y) непрерывна в огранич. замкнутой обл-ти D, то для этой ф-ции сущ.ДИ, т.е. сущ. предел интегр. суммы и этот придел не зависит не от сп-ба разбиения, не от выбора точек.

1*постоянный множитель выносится

2*интеграл от суммы равен сумме интегралов

3*если функция >=0 в области D,то и интеграл >=0.

4*область D можно разбить на D₁,… и интегралы сложить…

5*даны 2 функции. Если 1>=2, то и интеграл 1>=2

3* Вычисление двойного интеграла в декартовой с-ме коор.

Сводится к повторным.

1) чертим область интегрирования исходя из уравнений

2)определяем порядок интегрирования

3)находим верхние (левые) и нижние (правые) точки

4)определяем пределы внешнего интеграла

5)для нахождения пределов внутреннего интеграла проводим прямую II оси, одноименной с внутренней переменной.

4* Замена переменных в двойном интеграле. Переход в ДИ от декарто­вых к полярным координатам.

При вычислении интегралов часто бывает удобно сделать замену переменных. , где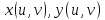,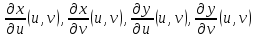непрерывны в некоторой областиПусть при этом формулы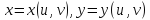задают взаимно-однозначное отображение областей:.Кроме того, не стремясь к минимальности условий, потребуем, чтобы всюду на области:

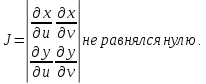
При сформулированных выше условиях для непрерывной на D функции 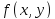справедливо:

Формула перехода от Декартовой к полярной системе:

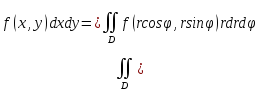
5* Приложения двойного интеграла - площадь плоской фигуры, объемы тел, ста­тические моменты и центр тяжести. Момент инерции плоской фигуры

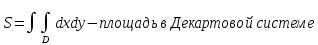
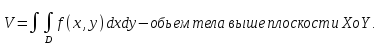
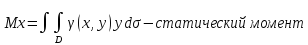
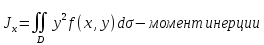
6* Тройной интеграл: определение, свойства, вычисление в декартовых координатах

Рассмотрим фигуру, представляющую собой пространственное тело V. Мерой этого тела будет являться его объем, который обозначим также буквой V. В теле V определена функция. Введем понятие тройного интеграла по этому телу. Для этого разобьем телоV произвольным образом на части . В каждом из полученных объемовпроизвольно выберем точку, вычислим значение функции в этих точкахи составим интегральную сумму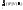. Обозначим черези перейдем к пределу в интегральной сумме при. Предел данной интегральной суммы назовемтройным интегралом от функции 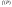по телуV:

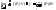
Для тройного интеграла остаются справедливыми все свойства интеграла по фигуре: линейность, аддитивность, теорема об оценке, теорема о среднем, и т.д.

7* Цилиндрические и сферические координаты. Переход в тройном интеграле от декар­товых к цилиндрическим и сферическим координатам

Положение точки в пространстве можно однозначно задать проекцией точки на плоскость x0y и аппликатой z. Проекцию же точки на плоскости x0y можно задать как в декартовых, так и в полярных координатах. Если проекцию точки задавать в полярных координатах, то в пространстве полученные координаты точки назовем цилиндрическими.

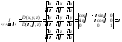
В цилиндрических координатах:

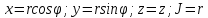
В сферических координатах: