Высшая математика / 2 / шпоры матем 31-39

31.Интервальные оценки параметров распределения.

Пусть Ө(хи) неизвестн. Параметр,а Ө* его не смещённая оценка.Точечные оценки дают хорошие результаты для больших объёмов выборок. Для малых выборок n<30 используются оценки определяемые 2умя числами –концами интервала внутри к. находится неизвестн. Параметр.Очевидно, что оценка Ө* будет чем точнее, чем меньше разность |Ө-Ө*|,т.е.чем меньше число б ,такое что|Ө-Ө*|<б .Данное неравенство раскрывая модуль можно записать: |Ө-Ө*|<б <=> Ө*-б <Ө<б+ Ө*.Статистич.методы не позволяют строго утверждать выполняется данное неравенство или нет.О выполнении равенства можно судить с определённой долей уверенности или вероятности,кот.назыв. доверительной вероятностью r (гамма).r= Р(|Ө-Ө*|<б ).При решении задачrзадаётся заранее и как правило=0,9;0,95;0,99.Интервал в к.находится Ө-доверительный интервал.

32.Условные варианты. Условные эмпирические моменты.

Усл.варианты. Предположим, что варианты выборки расположены в возрастающем порядке,т.е.в виде вариационного ряда.Равноотстоящими назыв.варианты,к.образуют арифметич.прогрессию с разностью(h).Условными назыв.варианты определяемые равенством U_i=( х_i -с )/ h, С-ложный ноль,h-шаг между любыми соседними первоначальными вариантами.Усл.эмпирич.моменты.Вычисление центральных моментов достаточно громодко, поэтому заменим первонач.варианты условными.Условн. эмпирич.моментом порядка(к)назыв.начальный момент порядка(к) вычисленный для усл.вариант : М_к*=(∑n_i u_i^k) /n=(∑n_i × ( х_i -с / h)^к)/h. В частности М₁*=(∑n_i *( х_i -с/h)¹)/h=1/h((∑n_i х_i )/n)-(∑n_i с/n))=1/h(х̅_в –с), выразим х̅_в => х̅_в = М₁*× h+с. Аналогично рассуждая получим Dв=( М₂*-( М₁*)²) × h².

33.Обычные,начальные и центральные эмпирич.моменты.

Обычные эмпирическим моментом порядка(к) назыв. ср.значение (к-х) степеней разности(х_i-с): М’_k=(∑n_i × ( х_i –с)^k)/n,где х_i-наблюдаемые варианты, n_i-частоты соответствующих вариант, n-объём выборки, с-ложный ноль. Начальным эмпирич.моментом порядка(к) назыв. обычный момент порядка(к) при (с=0): М_к=∑n_i х^к_i/ n в частности М₁=∑n_i х¹_i/ n= х̅_в т.е.начальный эмпирический момент 1-ого порядка= х̅_в. Центральным эмпирич.моментом порядка (к)наз.обычный момент порядка (к) при(с= х̅_в): m_k=∑n_i(х_i- х̅_в)^к/n в частности m₂=∑n_i(х_i- х̅_в)²/n= Dв т.е. центр. эмпирич.момент 2-ого порядка = Dв. Легко вывести,что m₂= М’₂-( М’₁)² ; m₃= М’₃-3 М’₂ М’₁+2(М’₁)³ ; m₄= М’₄-4 М’₃ М’₁+6М’₂(М’₁)²-3( М’₁)⁴

34. Эмпирические и выравнивающие частоты для дискретного распределения.

Рассмотрим дискретн. СВ(х) закон распределения к. не известен.Пусть произведено (n) испытаний в к. СВ(х)приняла(n₁) раз значение(х₁),( n₂)раза значение(х₂)и т.д. при чём сумма(n_i= n).эмпирич.частотами –назыв. фактически наблюдаемые частоты(n_i)-ые.Пусть имеется основание предположить,что изучаемая величина(х) распределена по некоторому опред.закону .Чтобы проверить согласуется ли это предположение с данными наблюдений вычисляют частоты наблюдаемых значений т.е.находят теоретические частоты (m_i)каждого из наблюдаемых значений предположении,что величина(х)распределена по данному закону.Выравнивающими частотами назыв-я числа (n_i) к-ое находится из равенства n’_i= nP_i , где n-число испытаний, P_i-вероятность наблюдаемого значения (х_i) вычисленное при допущении,чтоСВ(х)имеет предполагаемое распределение.Таким образом выравнивающая частота наблюдаемого значения (х_i)дискретного распределения равна произведению числа испытаний н вероятность этого наблюдаемого значения.

35. Эмпирические и выравнивающие частоты для непрерывного распределения.

В случае непрерывного распределения признака (х) ген.совокупности вероятности отдельных возможных значений(=0),поэтому весь интервал возможных значений разбивают на (к)интервалов и находят вероятности (P_i) попадаются СВ (х) в итый частичный интервал, затем, как и для дискретного распределения умножают число испытаний на эти вероятности. Таким образом выравнивающие частоты непрерывного распределения нах. по ф. : n’_i= nP_i . Для нормально распределённой СВ (х) формула запишется в виде: n’_i= nP_i=nh/٧_B×фи(u_i), где u_i= (х_i- х̅_в)/ ٧_B.

36. Условные средние. Выборочные уравнения регрессии.

При изучении двумерной СВ (ху)рассматривают не только числовые хар-ки одномерных компонент.(х)и(у) но и числовые хар-ки условных распределений. Условным мат. Ожиданием СВ (у) назыв. её мат.ожидание вычисленное при условии, что СВ(х) приняла опред.значение.Р_Х=х(У)=Р(У\Х_=Х) \-вычитание. Для дискретной СВ(х) и (у)условные мат.ожидания вычисляются по формулам М(У\х)=∑_УIР(У_I\х_I) ; М(Х\у)=∑_хIР(Х_I\у_I).В качестве оценок условных мат.ожиданий принимают условные средние к.находятся по выборке.Условным средним(у̅_х)назыв.ср. арифметическое наблюдавшихся значений(У)соответствующих(Х=х).Условным ср.( х̅_у)назыв.ср.арифметич.наблюдавшихся значений (Х)соответствующих(У=у)

37. Выборочные ур-я прямой линии регрессии по несгруппир. данным

Пусть изучаемая система количественных признаков(Х,У) в результате (n)испытаний получены пары чисел(х₁;у₁);(х₂;у₂)…(х_n;у_n).Предположим ,что выборочная регрессия (Уна х)является линейной и будем искать уравнение выборочной регрессии в виде: у̅_х=(кх+b),где к и в подлежат пределению.Параметр (к)(условный коэф-т прямой)назыв.выборочным коэф.(Уна х).Подберём параметры к и b так,чтобы точки построенные по данным наблюдений лежали на плоскости О_ху как можно ближе к прямой.Для этого воспользуемся методом наименьших квадратов. Назовём отклонением разность(у̅_х-у_i),где у̅_х-вычесленное по ур-ию у̅_х=кх+ b ордината при соответствующих значениях (х_i).Подберём параметры к и в таким образом,чтобы сумма квадратов отклонений была мин.для этого составим функцию F(k;b)=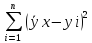=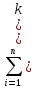)² Для определения минимума функц. найдём стационарные точки: 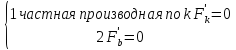; 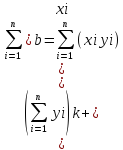Полученная система явл-я линейной относительно переменных (k) и (b),решив её например методом Крамера получим значения (k) и (b) и составим выборочное уравнение регрессии (У на х).

38. Выборочные уравнения прямой линии регрессии по сгруппированным данным.

При большом числе наблюдений одно и тоже значение(х) может встретиться (n_х)раз.Одно и тоже значение(у)-( n_у) раз.Одно и тоже значение (х,у)-( n_ху) раз.Поэтому данные группируют, подсчитывают частоты и сгруппированные данные вносят в таблицу,кот.назыв.корреляционной.Введём обозначения : ∑ х_i=n х̅_в=n х̅ ; ∑ у_i=n у̅_B=n у̅ ; ∑ х²_i=n х̅²_B=n х̅² ; ∑ х_i у_i=n_xyx_iy_i=> х̅у̅ =1/n∑ х_i у_i n_xy Тогда система для нахождения параметров (k) и (b) примет вид : 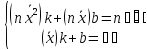; b= у̅- х̅k подставим в линейное уравнение у̅_x=kx+b и получим у̅_x=k_x+ у̅- х̅k преобразуем уравнение у̅_x- у̅=k(x- х̅) Из системы выразим коэф(k): k=( n х̅у̅- n х̅ у̅)/( n х̅²- n (х̅)² )= (х̅у̅ - х̅ у̅)/( х̅²-(х̅)²)= (х̅у̅ - х̅ у̅) / (٧_х)².

39. Выборочный коэф. корреляции . Коэф.детерминации.

Выбор.коэф.корреляции назыв величина r_в= (х̅у̅- х̅ у̅)/ ٧_х٧_у, | r_в |≤1, Уравнение прямой регрессии(Ух) может быть записано в виде у̅_x-у̅= r_в(٧_у/٧_х)(х- х̅).Уравнение прямой регрессии(Х_у): х̅_в- х̅= r_в(٧_х/٧_у)(у- у̅).Замечание: Прямые регрессии(Ух) и (Ху) разные,обе проходят через точку с координатами(х̅; у̅).Чем меньше угол между прямыми, тем теснее линейная зависимость между(х)и (у).Известно, что если прямые(х) и (у) ген.совокупности независимы,то их коэф.корреляции rг=0,Если же коэф корреляции ген. совокупности =±1, то х и у связаны функциональной зависимостью.Выборочный коэф.корреляции явл-я оценкой коэф-та корреляции ген.совокупности и поэтому так же служит для измерения линейной связи между признаками х и у.Для проверки нулевой гипотезы составляем выборочную статистику.затем по таблице критич.точек распределения Стьюдента находим tкр(α;n-2)Если|tнабл|<|tкр|,то гипотезу Н0-принимаем,иначе-отвергаем и принимаем альтернативную гипотезу Н1.Число (r²_в)-называется коэф.детерминации, оно определяет долю рассеивания, наблюдаемых значений СВ(У) относительно значений полученных их уравнения регрессии(Ух).Остальная доля отклонений может быть вызвана либо случ.ошибками,либо тем, что линейная регрессионная модель плохо согласуется с экспериментальными данными.