85 Тишин в. И. Основные методы решения тригонометрических уравнений

Тишин В. И.

Основные методы

решения

тригонометрических

уравнений

2003 г.

Материал подготовлен учителем математики Тишиным Владимиром Ивановичем.

2003 года

Содержание

Тригонометрические уравнения 4

1. Метод разложения на множители 4

Задание 1 20

2. Метод замены переменных и сведение к алгебраическим уравнениям 20

2.1. Применение формул двойного и половинного аргумента 25

2.2. Применение формул приведения 31

Задание 2 35

3. Уравнения, однородные относительно и 36

3.1. Применение формул приведения 40

Задание 3 43

Задание 4 47

4. Метод замены переменных 48

4.1. Замена . 48

Задание 5 53

4.2. Замена 53

4.3. Случаи, когда в уравнении не содержится 56

4.4. Случаи, когда аргументы кратны 2x и x 58

Задание 6 60

4.5. Замена . Универсальная тригонометрическая подстановка 60

Задание 7 68

5. Метод оценки левой и правой частей уравнения 69

Задание 8 74

6. Введение вспомогательного аргумента 75

Задание 9 78

7. Системы тригонометрических уравнений 79

Задание 10 81

Задание 11 83

Ответы 84

К заданию 1 84

К заданию 2 84

К заданию 3 84

К заданию 5 84

К заданию 6 85

К заданию 7 85

К заданию 9 85

Тригонометрические уравнения

1. Метод разложения на множители

Пример 1. Решите уравнение .

Решение

Преобразуем уравнение. Применим формулу:

.

Получим уравнение: .

Это уравнение решим разложением на множители: .

Получим совокупность уравнений:

.

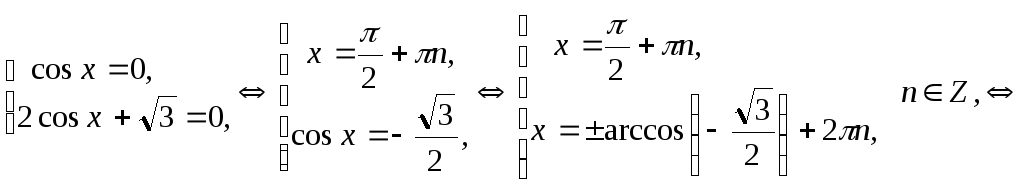
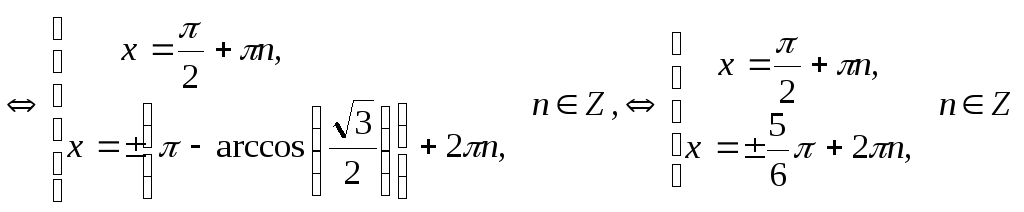Ответ: .

Пример 2. Решите уравнение

Решение

Преобразуем уравнение:

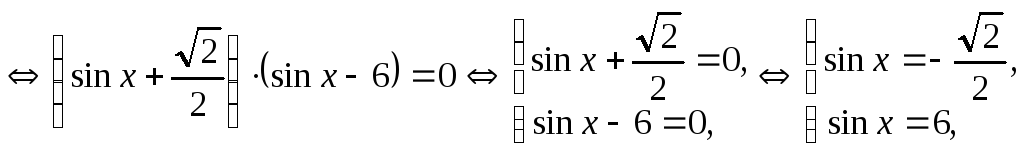
- решений не имеет.

Ответ: .

Пример 3. Решите уравнение

Решение

Преобразуем уравнение. Применим формулы:

и .

Получим уравнение:

.

Получим совокупность двух уравнений:

(1) и (2).

Уравнение (1) является однородным. В нем. В самом деле, если допустить противное, т. е., что, тогда, подставив его в уравнение (1), найдем, что и, что невозможно при одних и тех же значениях аргумента (в частности, не будет выполняться основное тригонометрическое тождество). Итак,.

Разделим обе части уравнения (1) на , получим.

Решим второе уравнение:

.

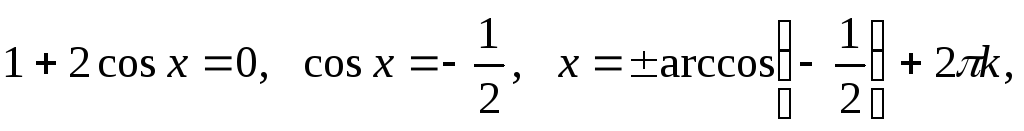
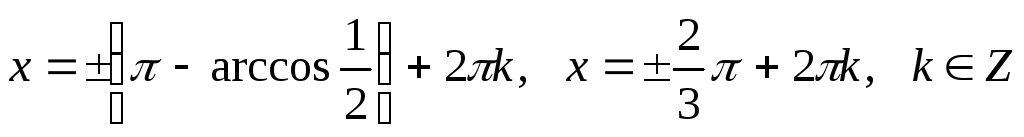Ответ: ,.

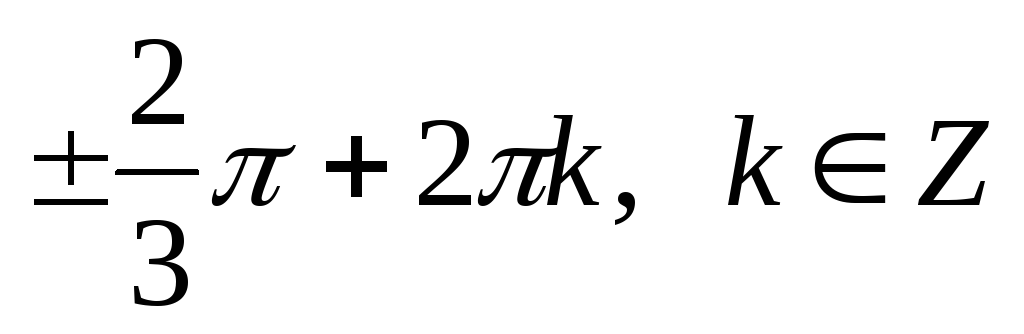Пример 4. Решите уравнение .

Решение

Преобразуем уравнение.

Уравнение примет вид:

.

Полученное уравнение равносильно совокупности уравнений:

Объединим полученные решения, если это возможно. Попробуем выработать общие принципы для объединения нескольких решений в одно.

Объединим два последних решения в одно: - это значит, что при четных значенияхk из множества корней получаются корни, значит,являются общими решениями двух последних решений.

Далее, найдем общие решения .

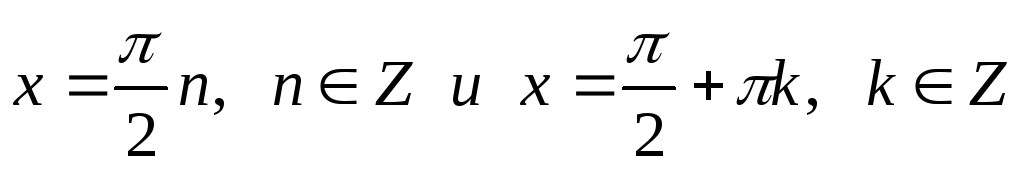, т. е. при нечетных значениях n из первого множества корней 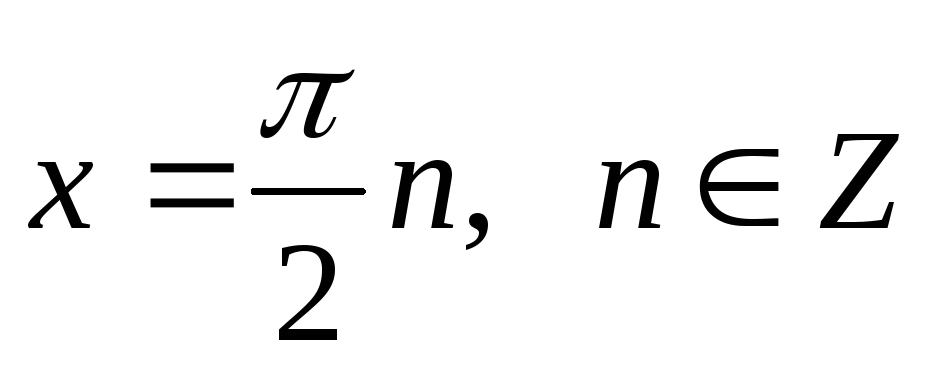получаются корни, следовательно,- являются общими решениями трех полученных результатов.

Ответ: .

Пример 5. Решите уравнение.

Решение

Преобразуем уравнение

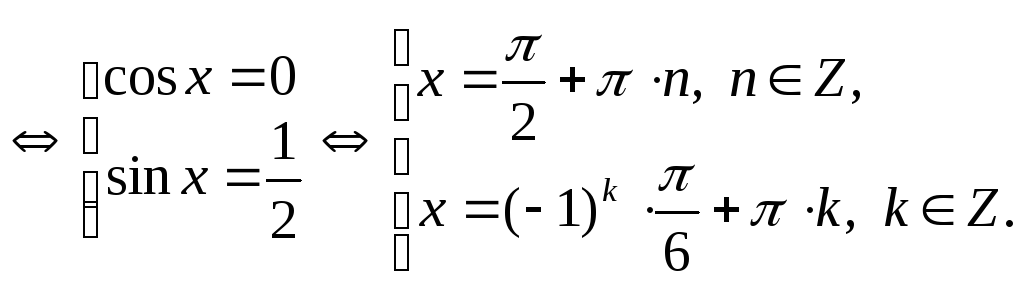
Ответ: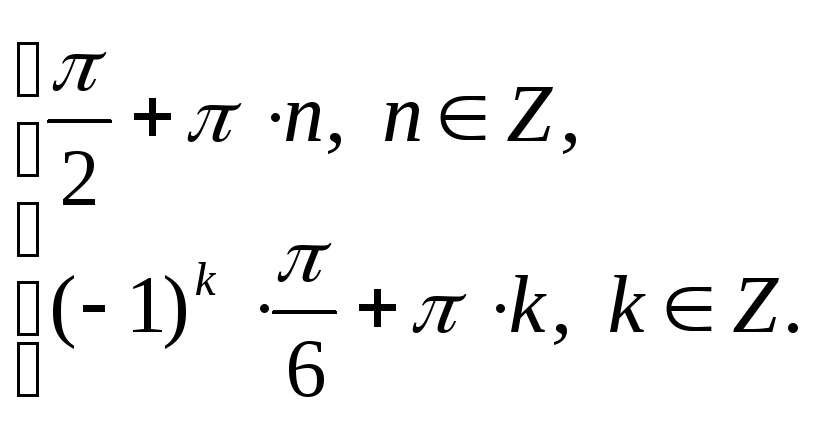

Пример 6. Решите уравнение

Решение

Преобразуем уравнение, для этого прибавим к левой части уравнения и вычтем, чтобы выражение не изменилось, произведение тогда уравнение примет вид

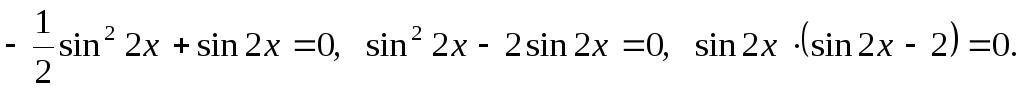
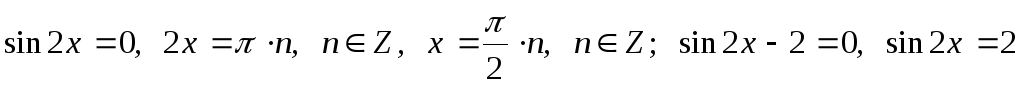- это уравнение не имеет решений, так как

Ответ: .

Пример 7. Решите уравнение .

Решение

I-й способ

Левая часть этого уравнения представляет собой однородное выражение относительно и. Уравнение было бы однородным, если бы в правой части уравнения был нуль.

Для преобразования уравнения в однородное, правую часть представим в виде: .

, а затем все перенесем в левую часть и приведем подобные слагаемые:

II-й способ

Преобразуем уравнение. Перенесем 25 из правой части в левую и сгруппируем с первым членом, получим:

.

Полученное уравнение равносильно совокупности двух уравнений:

Решая первое уравнение, находим: .

Второе уравнение является однородным первой степени,

Если допустить, что тогда подставив это значение в уравнение, получаем:. Но одновременноине могут равняться нулю. Итак,Разделим на него обе части уравнения, получим:

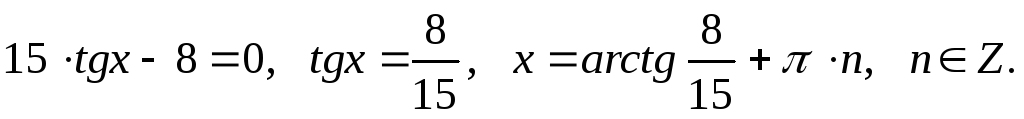
Ответ: ,

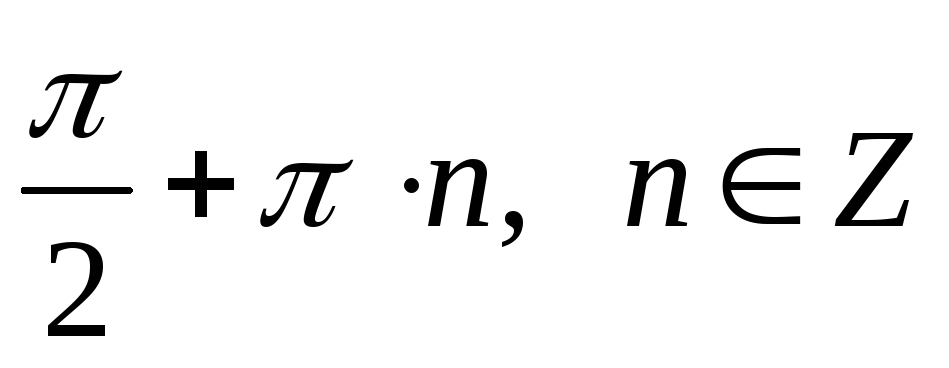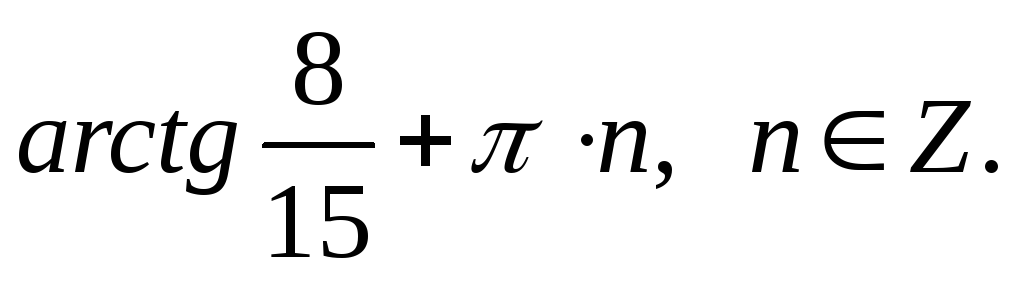
Пример 8. Решите уравнение

Решение

Область допустимых значений переменной: .

Преобразуем уравнение:

Это уравнение равносильно совокупности двух уравнений:

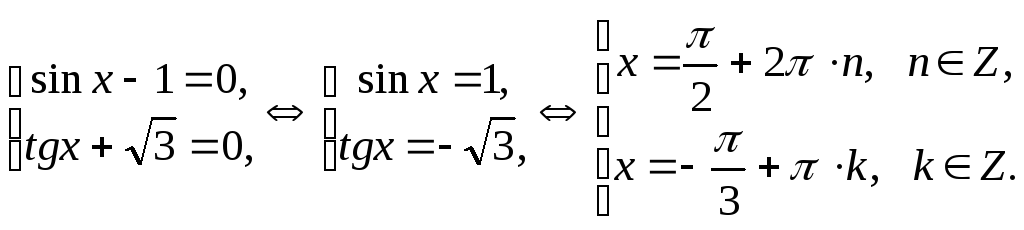
Определим, входят ли полученные значения в область допустимых значений.

Для этого, установим, найдутся ли такие целые значения n, k, m, при которых:

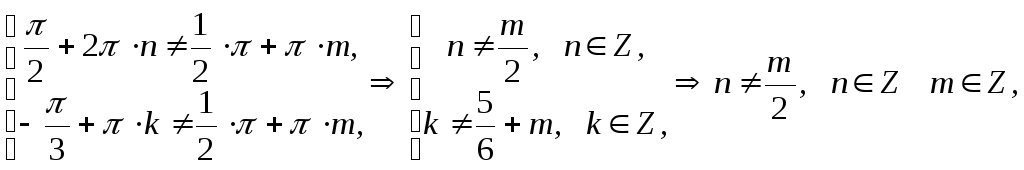
Отсюда следует, что первая группа корней не входит в область допустимых значений, т. е. .

Ответ: .

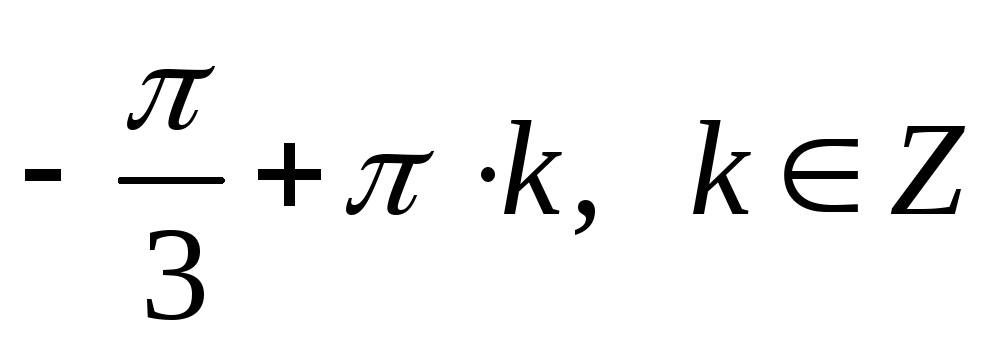Пример 9. Решить уравнение

Решение

Преобразуем разность синусов в произведение, получим

С учетом этого преобразования, уравнение примет вид

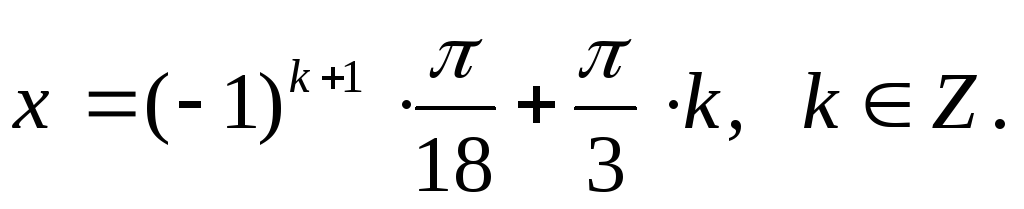
Ответ:

Пример 10. Решить уравнение

Решение

Преобразуем уравнение:

Получим совокупность уравнений:

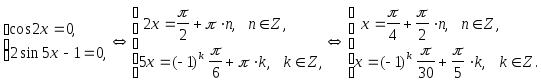
Ответ:

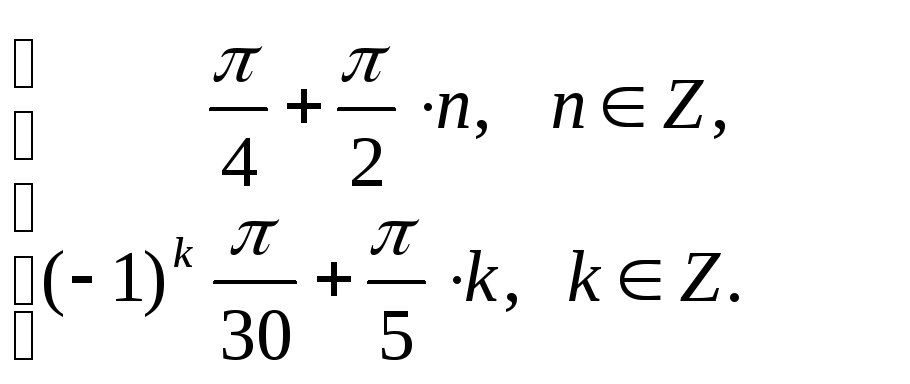
Пример 11. Решить уравнение .

Решение

Преобразуем уравнение, используя формулу , получим:

.

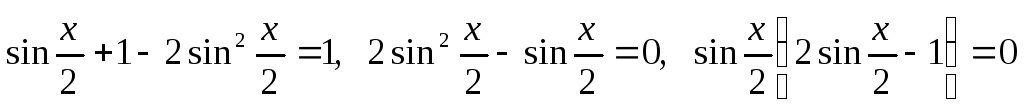Полученное уравнение равносильно совокупности уравнений:

Ответ: