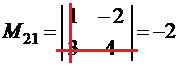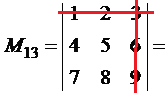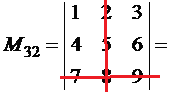Лекція 1 Определители

12

Лекція 1

Визначники та їх властивості

Визначники ІІ та ІІІ порядків. Визначники вищих порядків.

Алгебраїчні доповнення та мінори.

Правила обчислення визначників.

 

1.1. Означення. Матрицею називається таблиця чисел, що містить у загальному випадку m рядків та n стовпців:

,

де ; перший індекс і – номер рядка; другий індекс j – номер стовпця.

Якщо кількість рядків не дорівнює кількості стовпців (), то матриця називається прямокутною, якщо , то матриця називається квадратною.

Елементи , , …, квадратної матриці складають головну діагональ. Інша діагональ називається побічною.

Позначаються матриці великими літерами A, B, C і т.д. і записуються у круглих дужках.

Зауваження. Кожній квадратній матриці у відповідність можна поставити число, яке називається визначником і обчислюється за певним правилом. Для визначників невеликих вимірностей: та це правило приводить до зручних для запам’ятовування та використання схем. Тому з таких визначників ми і почнемо їх вивчення.

У літературі зустрічається багато позначень для визначників:

, , , , det A тощо.

Означення. Число, що виражає кількість рядків та рівну ним кількість стовпців, називають порядком визначника.

1.2. Визначники другого порядку.

Означення. Визначником другого порядку називається число, яке ставиться у відповідність таблиці чисел 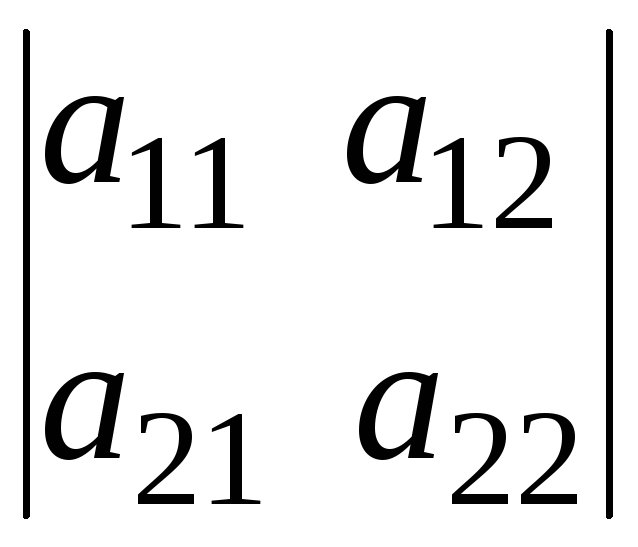і обчислюється за правилом:

.

(1.1)

Схематично правило (1.1) позначають так:

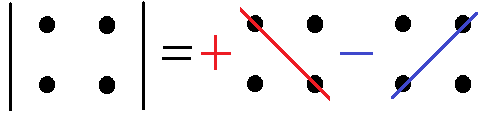
Рис. 1.1

Приклад. Обчислити визначник .

Розв’язання.

.

Основні властивості визначників

1. Якщо у визначнику елементи рядків замінити елементами стовпців, то значення визначника не зміниться.

Операція заміни елементів рядків елементами стовпців називається транспонуванням. Отриманий у результаті її виконання визначник називається транспонованим і позначається верхнім індексом Т:

, , , і т.д.

Доведення.

За означенням . Транспонований визначник дорівнює: . Співпадіння їх значень є очевидним.

2. Якщо у визначнику усі елементи будь-якого рядка (стовпця) дорівнюють нулю, то такий визначник дорівнює нулю.

Доведення (на прикладі нульових елементів першого рядка).

.

3. Якщо у визначнику усі елементи будь-якого рядка (стовпця) дорівнюють відповідним елементам іншого рядка (стовпця), то такий визначник дорівнює нулю.

Доведення (на прикладі рівних елементів рядків).

.

4. Якщо у визначнику усі елементи будь-якого рядка (стовпця) пропорційні відповідним елементам іншого рядка (стовпця), то такий визначник дорівнює нулю.

Доведення (на прикладі пропорційних елементів стовпців).

.

5. Якщо у визначнику переставити місцями два рядки (стовпці) то значення визначника зміниться на протилежне за знаком.

Доведення (на прикладі перестановки елементів рядків).

За означенням .

Після перестановки рядків отримаємо визначник:

.

6. Якщо всі елементи деякого рядка (стовпця) визначника помножити на число 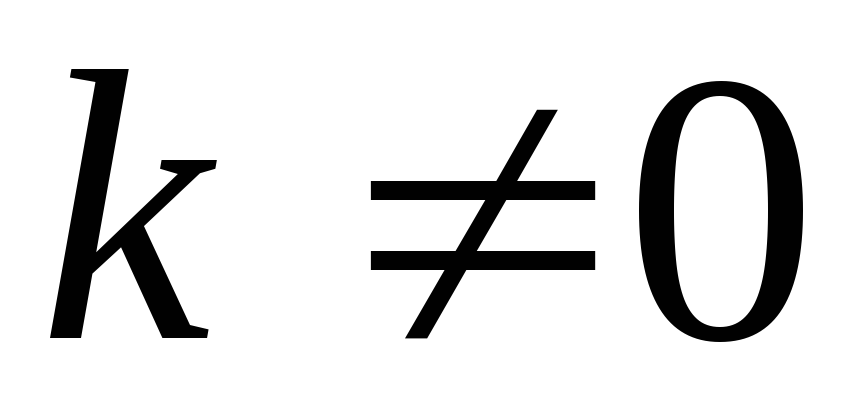, то значення визначника теж помножиться на це число.

Властивість 6 може бути сформульована у інший спосіб: спільний множник елементів будь-якого рядка (стовпця) можна виносити за знак визначника.

Доведення (на прикладі елементів другого стовпця).

.

7. Якщо всі елементи і-го рядка визначника записати у вигляді суми двох додатків 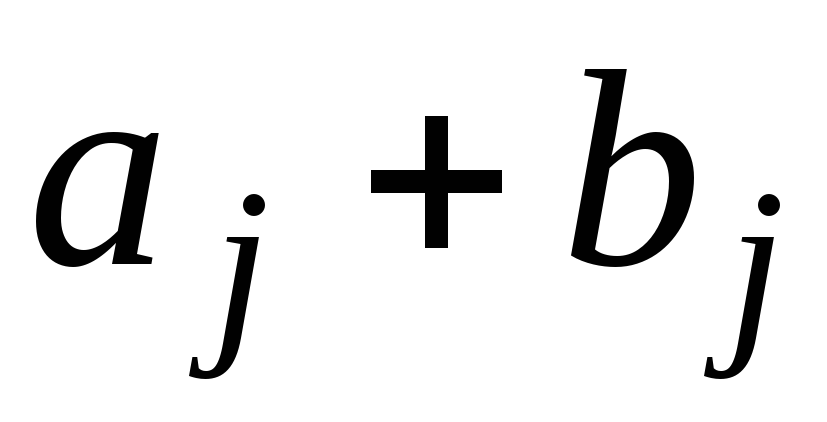, то такий визначник дорівнює сумі двох визначників, у яких всі рядки, крім і-го, такі самі, як і в початковому визначнику, і-й рядок одного з визначників складається з елементів а_j, а другого – з елементів b_j.

Доведення (на прикладі елементів першого рядка).

Для елементів першого рядка твердження властивості набуває вигляду:

.

Обчислимо визначник:

.

8. Значення визначника не змінюється, якщо до елементів одного з рядків додаються елементи другого рядка, помножені на одне й те саме число.

Доведення (на прикладі рядків).

Для елементів рядків твердження властивості набуває вигляду:

.

1.3. Визначники третього порядку.

Означення. Визначником третього порядку називається число, що обчислюється за правилом:

.

Це правило називається правилом трикутників. Його зручно запам’ятати за допомогою наступної схеми:

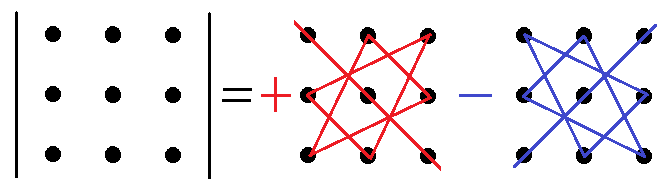
Рис. 1.2.

Приклад. Обчислити визначник .

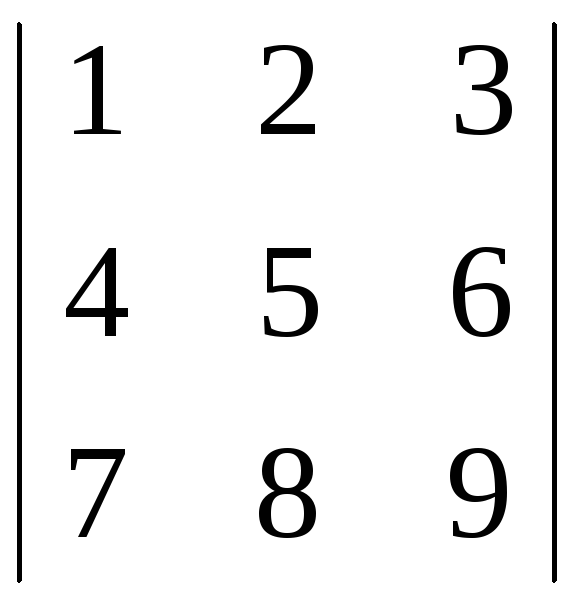Розв’язання.

.

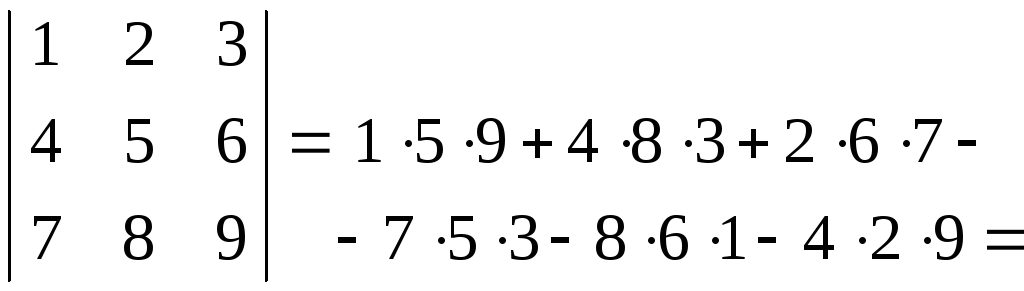
Зауваження. Для визначників третього порядку мають місце всі властивості, сформульовані для визначників другого порядку. Крім того, має місце ще одна властивість 9.

Властивість 9. Якщо усі елементи будь-якого рядка (стовпця) є лінійними комбінаціями відповідних елементів інших рядків (стовпців), то такий визначник дорівнює нулю.

Приклад. У визначника із попереднього приклада елементи першого (І) рядка можуть бути отримані як різниця подвоєного добутку елементів другого рядка та самих елементів третього рядка.

Нехай 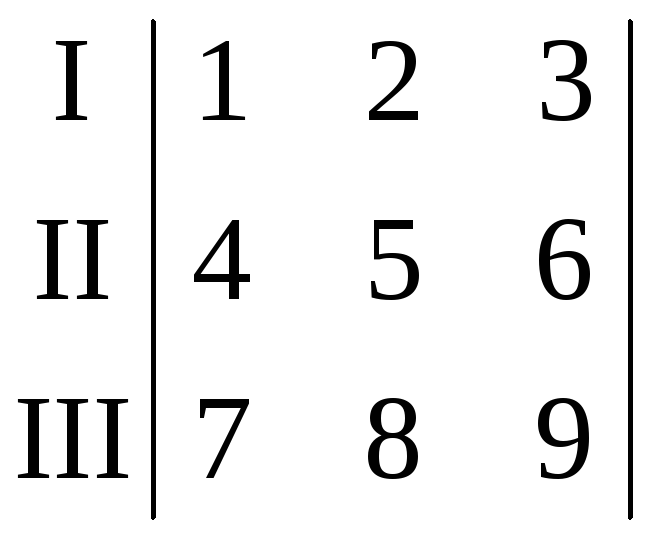. Тоді , а саме: .

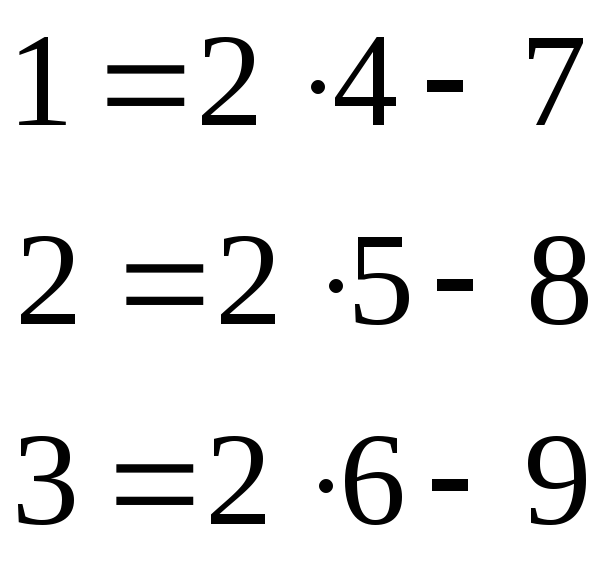Зауваження. Існує інша схема обчислення визначників третього і вищих порядків близька до метода трикутників. Ця схема називається правилом Саррюса. Полягає вона у тому, що до визначника дописують перші два стовпчики. Складають суму добутків елементів, що розташовані на діагоналях, які паралельні головній діагоналі. Від цієї суми відняти добутки елементів, що розміщені на діагоналях, паралельних побічній (рис. 1.2). Правило Саррюса можна використовувати для обчислення визначників довільного порядку n, приписуючи (n-1) стовпець.

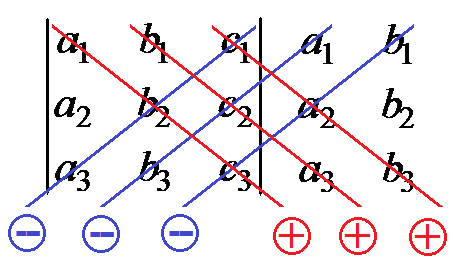
Рис. 1.2

Метод розкриття визначника за елементами рядка або стовпця

Означення. Мінором елемента називається визначник (n-1)-ого порядку, який утворюється із заданого визначника n-го порядку викреслюванням i-ої строки та j -ого стовпця.

Означення. Алгебраїчним доповненням елемента є добуток

.

Зауваження. Таким чином, коли показник степеня є парним, тоді значення мінора та алгебраїчного доповнення співпадають. Коли показник степеня є непарним, тоді значення мінора та алгебраїчного доповнення є протилежними числами.

Приклади обчислення мінорів та алгебраїчних доповнень.

Визначник	Мінор	Алгебраїчне доповнення

Теорема. Визначник порядку n дорівнює сумі добутків елементів будь-якого рядка (або стовпця) на їх алгебраїчні доповнення:

.

(1.2)

Зауваження. Записана теорема є окремим випадком більш загальної теореми, яка доведена Лапласом у 1772 р. Окремий випадок теореми Лапласа зустрічається ще раніше у рукописах Лейбніца.

Теорема Лапласа. Нехай А  — квадратна матриця розміру  в якій вибрано довільні k рядків (стовпців). Тоді визначник матриці  дорівнює сумі всіляких добутків мінорів -го порядку, розташованих в цих рядках (стовпцях), на їх алгебраїчні доповнення:

,

(1.3)

де підсумовування ведеться по всіх номерах стовпців (рядків) .

Число мінорів, по яких береться сума в теоремі Лапласа, рівне числу способів вибрати k стовпців з n, тобто біноміальному коефіцієнту .

Приклад. Розкрити визначник із приклада 1 за елементами другого стовпця.

Розв’язання.

.

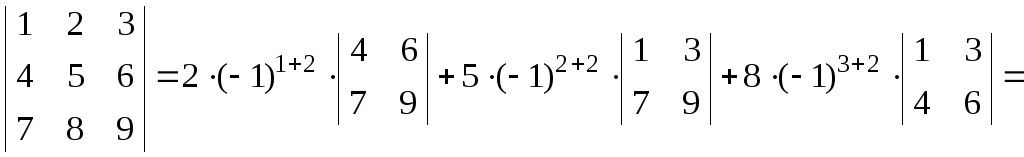
Обчислення визначника метод зниження порядку

Застосовуючи властивість 8, підбираючи при цьому значення множника k доцільним чином, можна усі елементи обраного рядка (стовпця), крім одного, перетворити на нулі. Тоді формула (1.2) буде містити лише один доданок.

Приклад. Обчислити визначник із першого приклада методом зниження порядку.

Розв’язання.

.

Обчислення визначника приведенням до трикутного вигляду

Застосовуючи властивість 8 по черзі до кожного з рядків (стовпців) визначник можна привести до трикутного вигляду, при якому усі елементи, що знаходяться вище або нижче однієї із діагоналей дорівнюють нулю. Тоді визначник дорівнює добутку елементів, що знаходяться на діагоналі.

Приклад. Обчислити визначник із першого приклада методом приведення до трикутного вигляду.

Розв’язання.

.

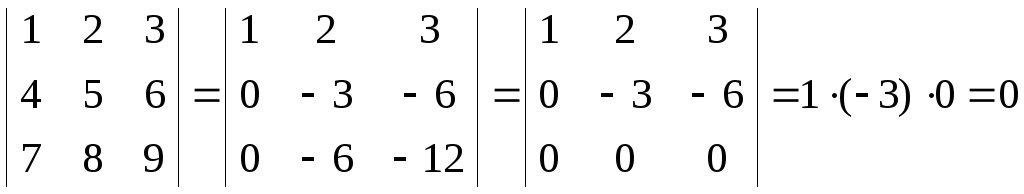1.3. Визначники вищих порядків

Означення. Визначником n-го порядку є число, яке дорівнює сумі добутків елементів визначника зі всіма можливими комбінаціями різних номерів рядків і стовпців (в кожному із добутків є рівно по одному елементу з кожного рядка і кожного стовпця). Кожному добутку приписується знак плюс чи мінус, в залежності від парності перестановки номерів.

Зауваження. Для визначників вищих порядків мають місце усі, сформульовані вище властивості.

Зауваження. При ручному обчисленні визначників вищих порядків доцільно застосовувати: метод зниження порядку, метод приведення до трикутного вигляду, метод Саррюса.
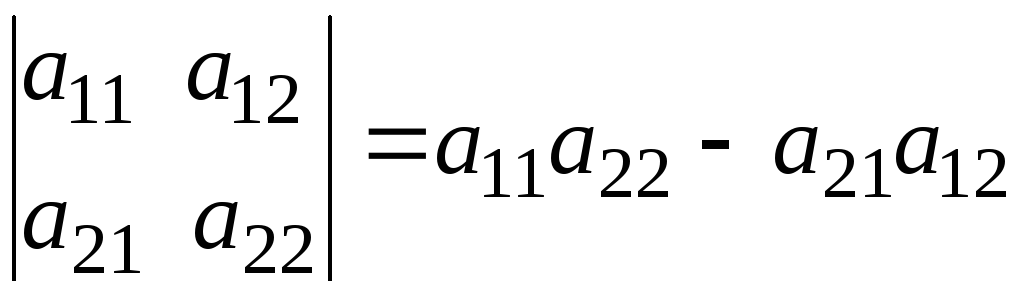