
Лекция 8
.docЛисенко В.І.
«Вища математика»
І КУРС
Опорні конспекти лекцій
Лекція №8. Прямі лінії та площини
Література:
-
Тевяшев А.Д., Литвин О.І. Вища математика в прикладах та задачах. Ч.І. – К.: Кондор, 2006. – 588 с. (с. 36-37, 45-50).
-
Данко П.Е. Высшая математика в упражнениях и задачах. Ч І.– М. 2005. –304 с. (с. 53-63).
-
Гусак А.А. Высшая математика: учебник для студентов вузов. В 2 т. Т.1. – Минск: ТетраСистемс, 2007 – 544с. (31-40 с.).
-
Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навчальний посібник: К.: Центр навч. Літератури, 2005 – 536с. (с. 103-109).
Основні теоретичні положення
Предметом аналітичної геометрії є вивчення геометричних образів алгебраїчними методами.
Кожна точка на площині ототожнюється з упорядкованою парою чисел, а в просторі – з упорядкованою трійкою чисел – координатами цієї точки.
-
Найпростіші задачі аналітичної геометрії:
а)
Відстань між двома точками
![]() та
та
![]()
Розв’язання
Обчислимо
координати вектора
![]() .
.
Знаходимо
довжину вектора
![]() .
.
![]() (1)
(1)
б)Поділ відрізка у заданому відношенні.
Нехай
кінці відрізка
![]() задані своїми координатами
задані своїми координатами
![]() та
та
![]() ,
а точка
,
а точка
![]() поділяє відрізок
поділяє відрізок
![]() у відношенні
у відношенні
![]() .
Тобто
.
Тобто
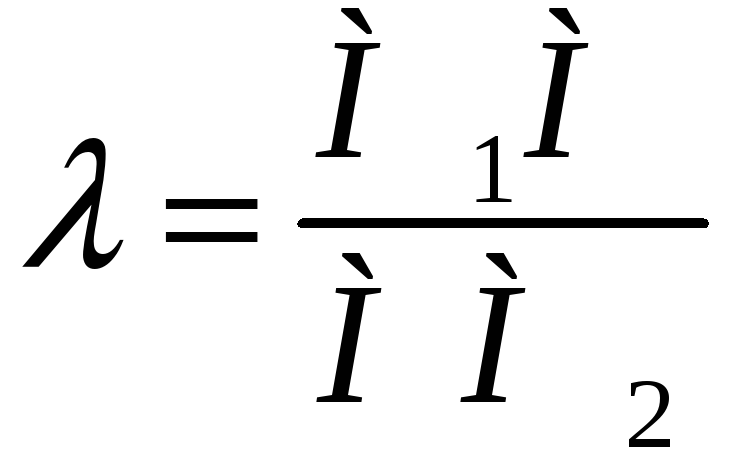 Інакше
це можна записати так:
Інакше
це можна записати так:
![]() .
Запишемо останню рівність у векторній
формі
.
Запишемо останню рівність у векторній
формі
![]() .
Звідки:
.
Звідки:
![]() ,
інакше
,
інакше
![]() .
.
На основі рівності векторів, маємо:


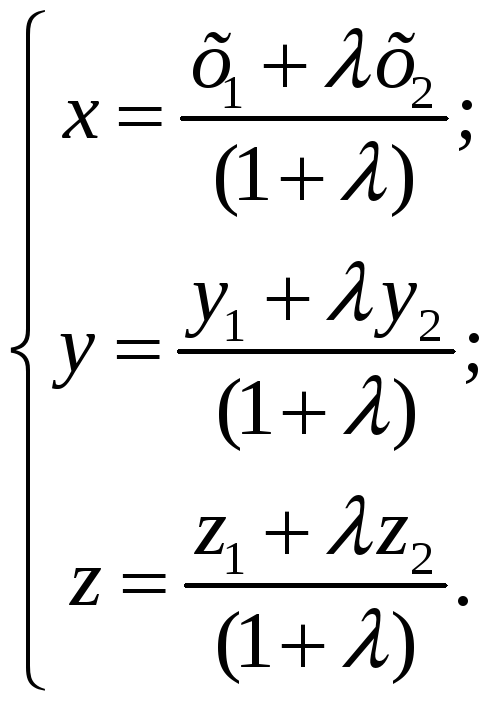 (2)
(2)
Якщо
точка М(x;y;z)
поділяє відрізок
![]() навпіл, тобто
навпіл, тобто
![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() (3)
(3)
Приклад
1. Знайти відстань між точками
![]() та
та
![]() ,
а також координати точки М, що поділяє
відрізок
,
а також координати точки М, що поділяє
відрізок
![]() у відношенні
у відношенні
![]() .
.
Розв’язання.
За формулою (1) маємо:
![]()
![]() .
Тоді
.
Тоді
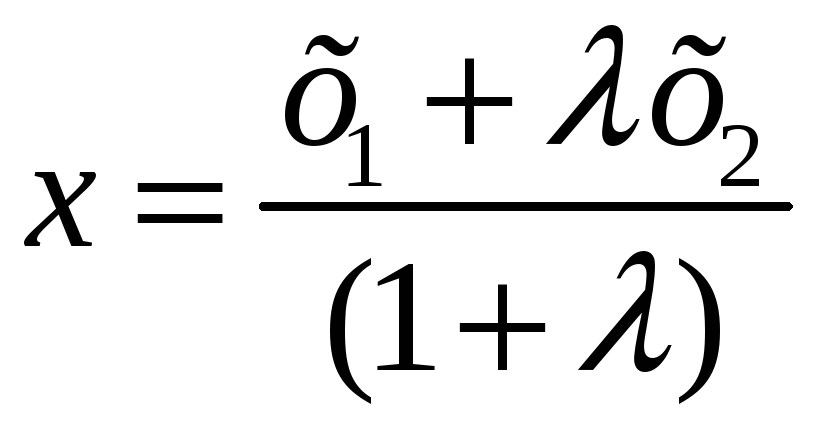 ;
;
 ;
;
 .
.
Тобто
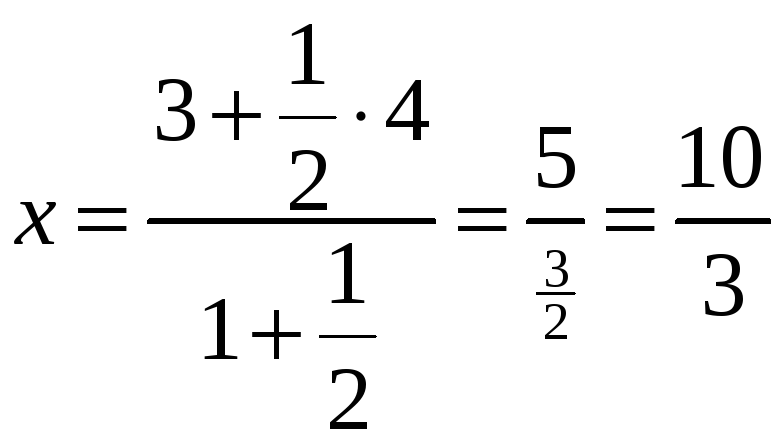 ;
;
 ;
;
 ;
;
![]() .
.
-
Основні задачі аналітичної геометрії
а) Складання рівняння геометричного об’єкта, який розглядають як геометричне місце точок.
б) Дослідження і побудова геометричного об’єкта за його рівнянням.
-
Пряма на площині
Означення:
будь-яке
рівняння першого степеня відносно x та
y
визначає на площині деяку пряму. Записують
![]() (3), де А, В, С – числові коефіцієнти,
причому А і В одночасно не дорівнюють
нулю.(записують
(3), де А, В, С – числові коефіцієнти,
причому А і В одночасно не дорівнюють
нулю.(записують
![]() )
)
Самостійно дома записати частинні випадки рівнянь прямих та побудувати їх графіки, якщо:
1)
![]() ;
;
![]() ;
;
![]() ;
;
2)
![]() ;
;
![]() ;
;
![]() ;
;
3)
![]() ;
;
![]() ;
;
![]() ;
;
4)
![]() ;
;
![]() ;
;
![]() ;
;
5)
![]() ;
;
![]() ;
;
![]() ;
;
Залежно від способу задання прямої на площині одержують різні види рівнянь, які систематизовані в таблиці 1.
Таблиця 1.
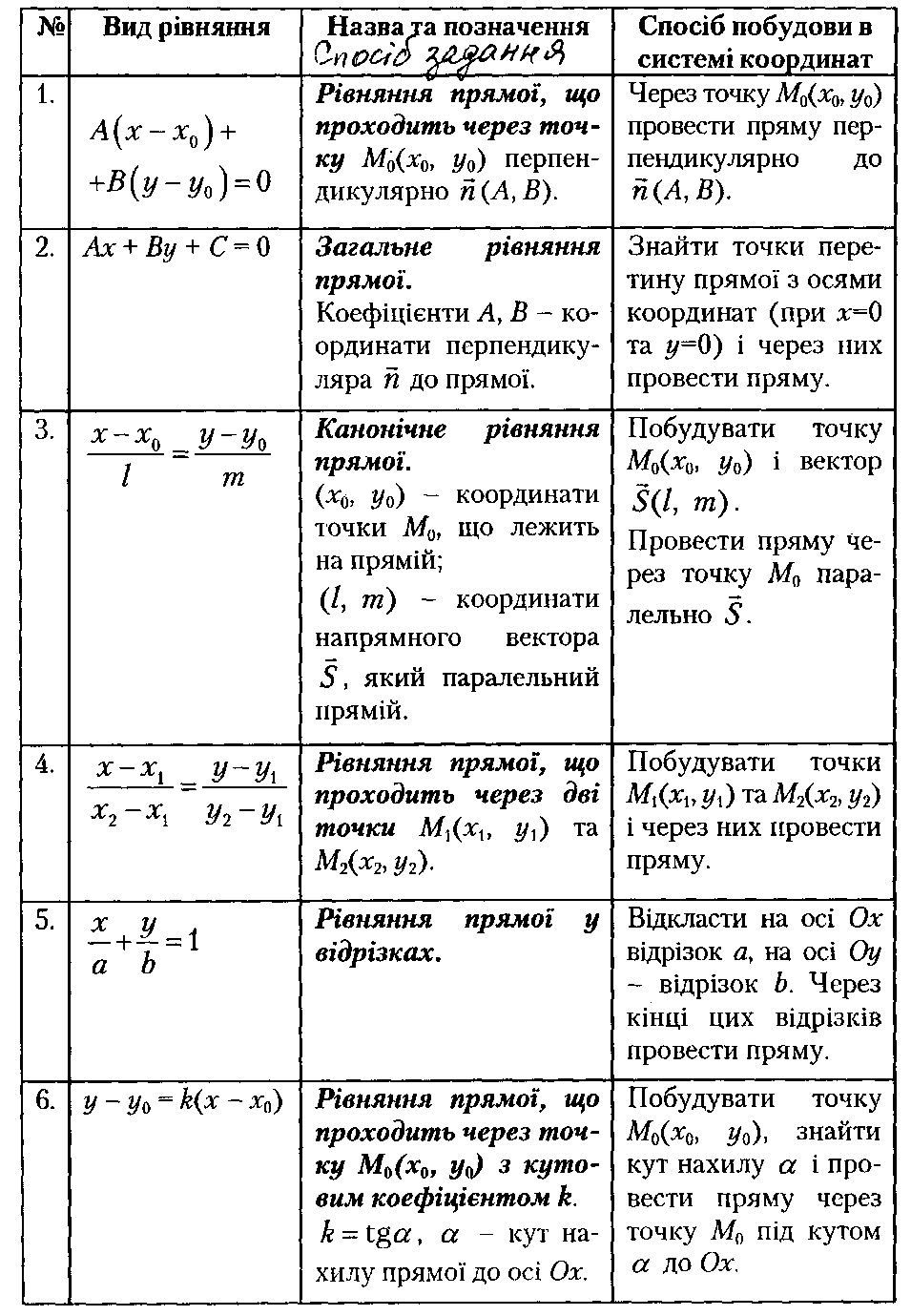
![]()

Примітка
1.
Щоб одержати рівняння прямої, що проходить
через точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() ,
треба на прямій вибрати точку
,
треба на прямій вибрати точку
![]() і записати скалярний добуток векторів
і записати скалярний добуток векторів
![]() та
та
![]() .
.
![]() .
.
2. Щоб
одержати канонічне рівняння прямої (чи
рівняння прямої, що проходить через дві
точки) треба записати в координатній
формі колінеарність векторів
![]() та
та
![]() (
(![]() та
та
![]() ).
).

![]()

![]()



Другий спосіб.
Зведемо задані рівняння до рівнянь прямої з кутовим коефіцієнтом

Тепер
тангенс шуканого кута
![]() можна знайти за формулою
можна знайти за формулою
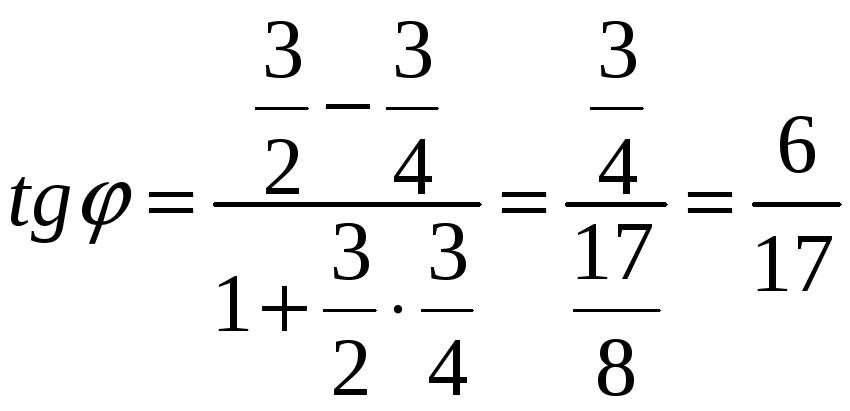 ;
;
![]()
Приклад 4.
Знайти
відстань між двома прямими:
![]() та
та
![]() .
.
Розв’язання
Прямі
задані загальними рівняннями є паралельні,
оскільки координати векторів,
перпендикулярних до цих прямих (
![]() та
та
![]() )
пропорційні.
)
пропорційні.
![]()
Знайдемо координати будь-якої точки, що задовольняє рівняння першої прямої.
Нехай
х=2, тоді
![]() ,
звідки у=2. тобто точка
,
звідки у=2. тобто точка
![]() належить першій прямій.
належить першій прямій.
За формулою (4) знаходимо її відстань від другої прямої (тобто відстань між паралельними прямими).
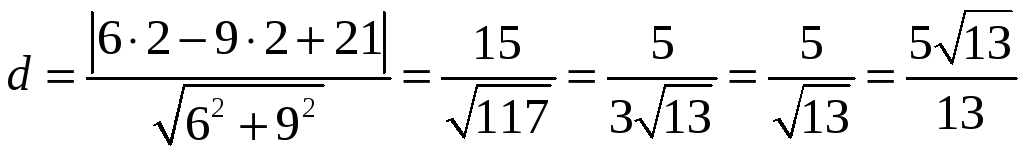
-
Пряма у просторі. Основні види рівнянь прямої у просторі.
-
Рівняння прямої, що проходить через дві точки
 та
та
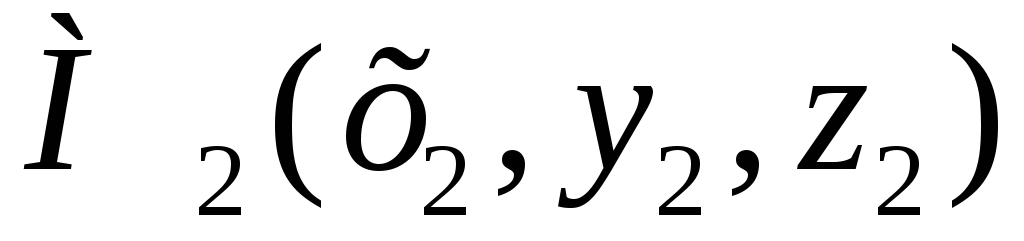
 (12)
(12)
-
Канонічне рівняння прямої, що проходить через точку
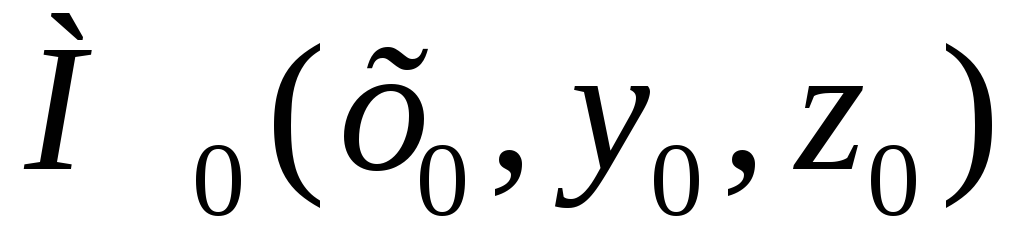 і має напрямний вектор
і має напрямний вектор
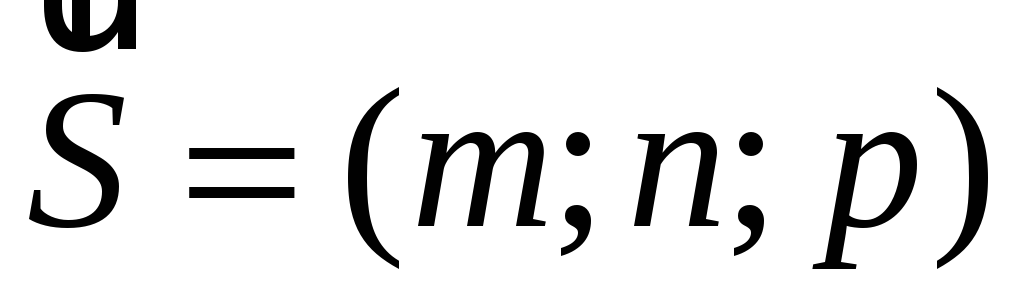
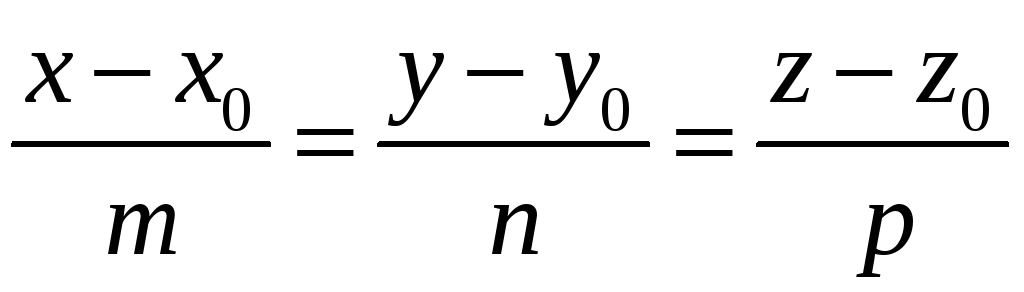 (13)
(13)
-
Загальне рівняння прямої, що визначена перетином двох непаралельних площин
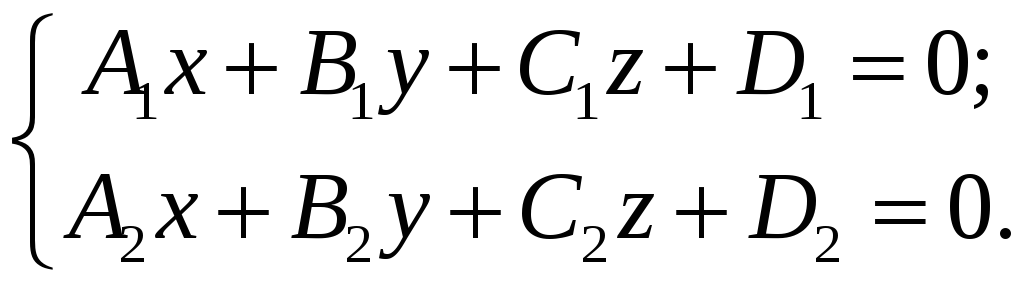 (14)
(14)
Приклад
5. Вершини трикутника АВС задані
координатами:
![]() ,
,
![]() ,
,
![]() .
Записати рівняння медіани АМ.
.
Записати рівняння медіани АМ.
Розв’язання
Користуючись формулами (3), знаходимо
Координати
точки
![]() як середини відрізка ВС.
як середини відрізка ВС.
 ;
;
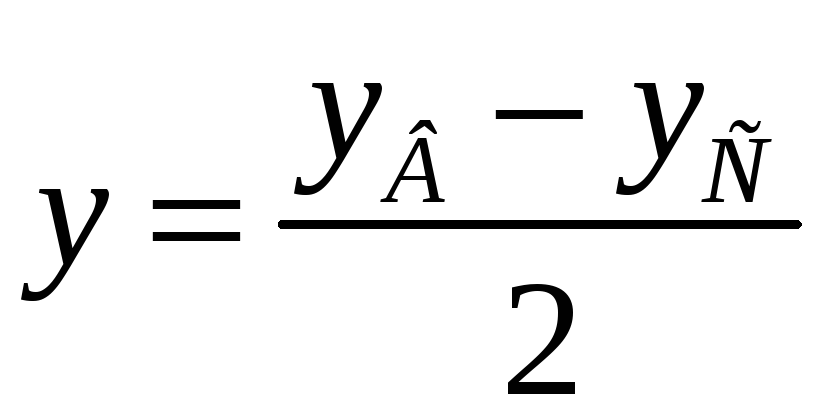 ;
;
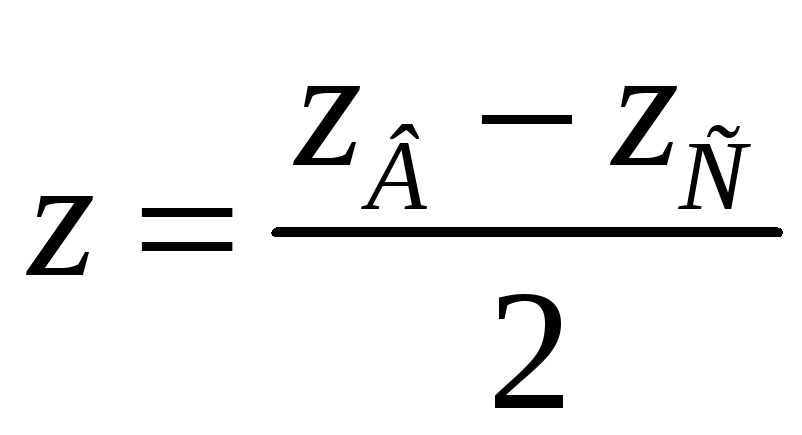 .
.
![]() ;
;
![]() ;
;
![]() .
.
Отже
![]() .
.
Скористаємось формулою рівняння прямої, що проходить через дві точки А та М.
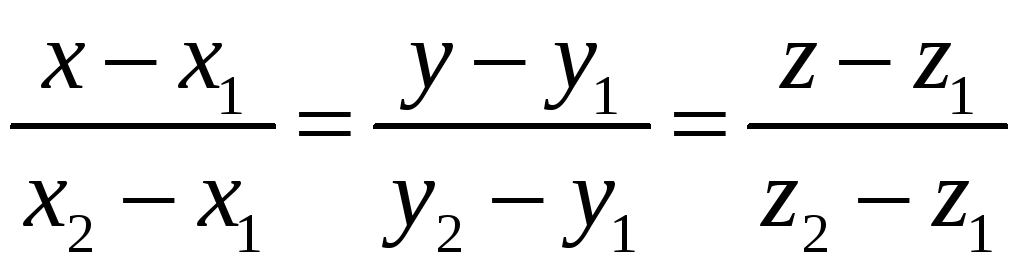 .
Одержимо
.
Одержимо
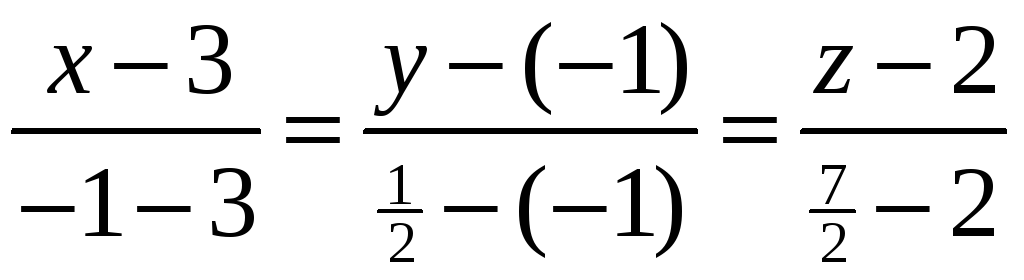 ;
;
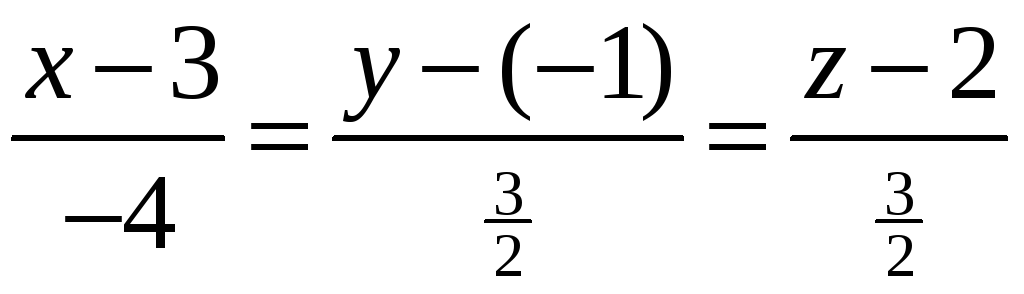
![]()
-
Види рівнянь площини.
а)
Рівняння
площини, яка проходить через точку
![]() перпендикулярно до вектора
перпендикулярно до вектора
![]() .
.
Нехай
точка
![]() належить цій площині. Тоді вектор
належить цій площині. Тоді вектор
![]() і
і
![]() перпендикулярні, а значить їх скалярний
добуток дорівнює нулю.
перпендикулярні, а значить їх скалярний
добуток дорівнює нулю.
![]()
![]() ;
;
![]() (1) –
(1) –
рівняння
площини, яка проходить через точку
![]() і має вектор нормаль
і має вектор нормаль
![]()
Якщо у формулі (1) розкрити дужки, то одержимо
![]() ї
ї
![]() (*)
(*)
Позначимо
![]() .
Тоді формула (*) матиме вигляд:
.
Тоді формула (*) матиме вигляд:
![]() (2) –
загальне рівняння площини.
(2) –
загальне рівняння площини.
Зауваження.
Вектор
![]() називають нормальним вектором або
вектором нормалі площини
називають нормальним вектором або
вектором нормалі площини
![]() .
.
Приклад 1.
Записати
рівняння площини, що проходить через
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() .
.
Розв’язання:
У формулу
(1) підставимо координати точки
![]() і вектора
і вектора
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Дослідимо загальне рівняння площини
![]()
-
Якщо D=0, то воно приймає вигляд
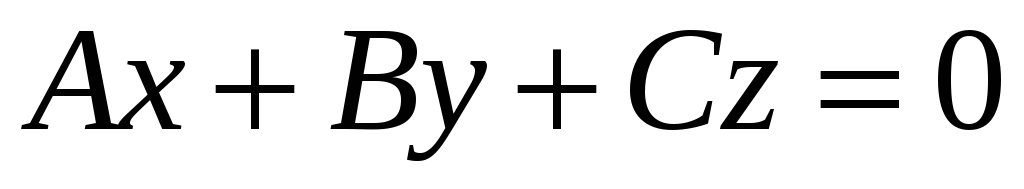 і визначає площину, що проходить через
початок координат. (Це рівняння
задовольняє точка О(0;0;0))
і визначає площину, що проходить через
початок координат. (Це рівняння
задовольняє точка О(0;0;0)) -
Якщо А=0, то рівняння (2) приймає вигляд
 і визначає площину, вектор нормалі якої
і визначає площину, вектор нормалі якої
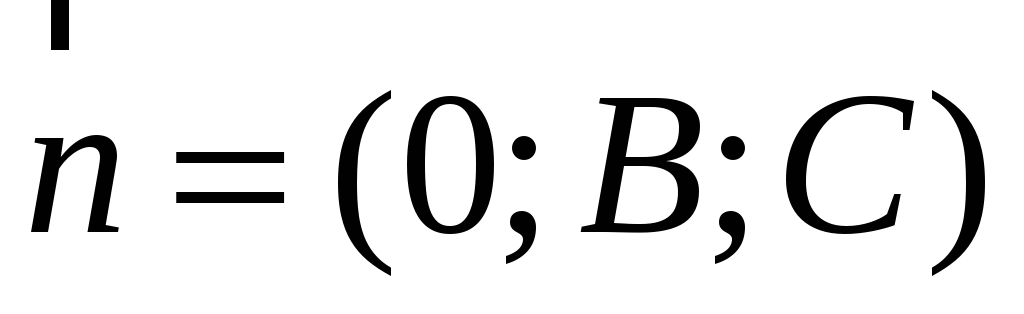 перпендикулярний осі Ox (Оскільки
перпендикулярний осі Ox (Оскільки
 ),
а значить площина паралельна до осі
Ox. Отже, якщо у загальному рівнянні
площини коефіцієнт при х дорівнює нулю,
площина
),
а значить площина паралельна до осі
Ox. Отже, якщо у загальному рівнянні
площини коефіцієнт при х дорівнює нулю,
площина
 паралельна до осі Ох.
паралельна до осі Ох.
Аналогічно, якщо:
В=0, то
площина
![]() паралельна осі Oy;
паралельна осі Oy;
С=0, то
площина
![]() паралельна Oz;
паралельна Oz;
А=В=0. то
площина
![]() паралельна до площини Оху;
паралельна до площини Оху;
А=С=0, то
площина
![]() паралельна до площини Охz;
паралельна до площини Охz;
В=С=0, то
площина
![]() паралельна до площини Оyz;
паралельна до площини Оyz;
A=D=0, то
площина
![]() проходить через Ох;
проходить через Ох;
В=D=0, то
площина
![]() проходить через Оу;
проходить через Оу;
С=D=0, то
площина
![]() проходить через Оz;
проходить через Оz;
А=В=D=0, то площина Сz=0 співпадає з Оху;
В=С=D=0, то площина Ах=0 співпадає з Оyz;
А=С=D=0, то площина Ву=0 співпадає з Охz;
Якщо у
рівнянні (2)
![]() коефіцієнт
коефіцієнт
![]() ,
то поділивши всі члени рівняння на
,
то поділивши всі члени рівняння на
![]() і позначивши
і позначивши
![]() ,
,
![]() ,
,
![]() ,
одержимо:
,
одержимо:
![]() ;
;
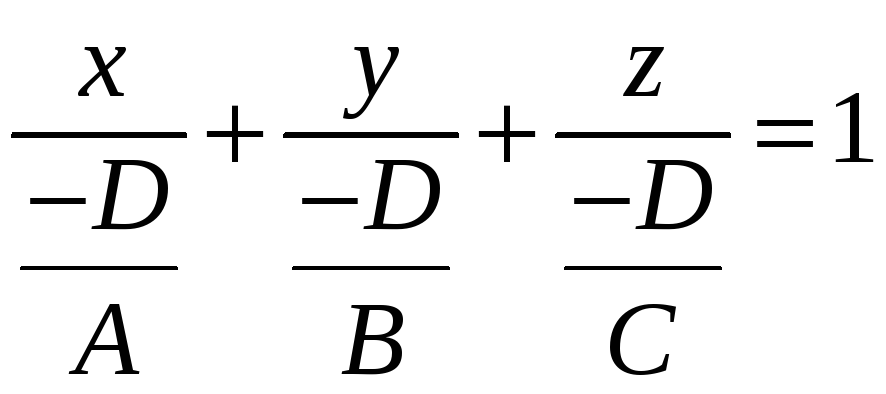 ,
тобто
,
тобто
![]() (3) –
рівняння площини у відрізках.
(3) –
рівняння площини у відрізках.
У цьому
рівнянні
![]() ,
,
![]() і
і
![]() – відповідно абсциса, ордината і апліката
точок перетину площини з осями Ох, Оу
та Оz.
– відповідно абсциса, ордината і апліката
точок перетину площини з осями Ох, Оу
та Оz.
Нехай
на площині задані три точки
![]() ,
,
![]() та
та
![]() .
Візьмемо на площині довільну точку
.
Візьмемо на площині довільну точку
![]() .
Оскільки всі чотири точки лежать на
площині, то вектори
.
Оскільки всі чотири точки лежать на
площині, то вектори
![]() ,
,
![]() та
та
![]() компланарні,
тому їх мішаний добуток дорівнює нулю.
компланарні,
тому їх мішаний добуток дорівнює нулю.
![]() (**)
(**)
Запишемо координати цих векторів
![]() ,
,
![]() ,
,
![]() .
Тоді рівність (**) прийме вигляд:
.
Тоді рівність (**) прийме вигляд:
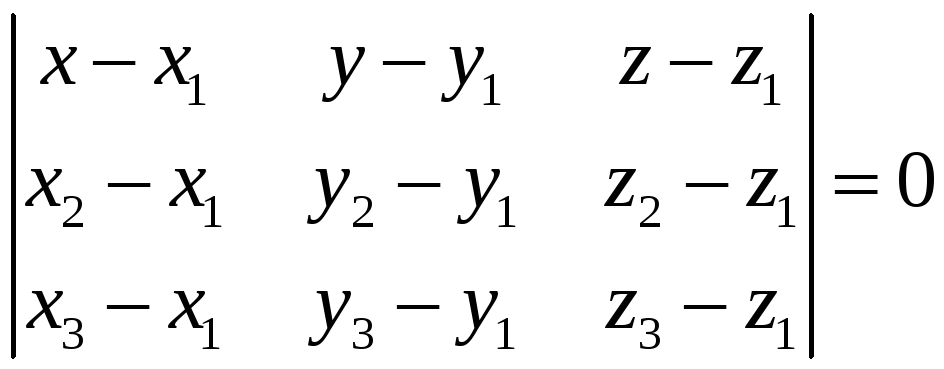 (4) –
(4) –
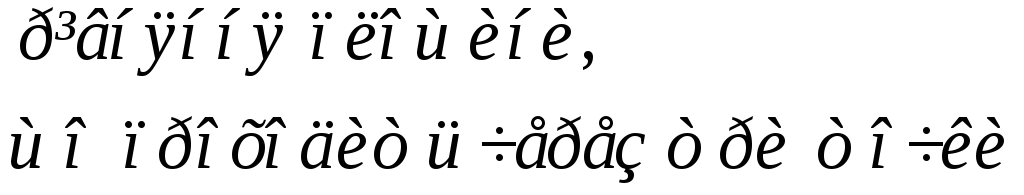
Приклад 2.
Записати
рівняння площини, яка проходить через
три точки
![]() ,
,
![]() ,
,
![]() .
.
Розв’язання:
Скористаємось формулою (4)
 ,
одержимо
,
одержимо
 .
.
Звідки:
![]() ,
тобто
,
тобто
![]() .
Поділимо почленно на
.
Поділимо почленно на
![]() .
Одержимо
.
Одержимо
![]() ,
тобто
,
тобто
![]() .
.
Нехай
![]() ,
,
![]() ,
,
![]() .
Тоді рівняння площини має вигляд
.
Тоді рівняння площини має вигляд
![]() ,
оскільки точки А, В і С лежать на осях
Ох, Оу та Оz.
,
оскільки точки А, В і С лежать на осях
Ох, Оу та Оz.
-
Кут між площинами. Умова паралельності і перпендикулярності двох площин.
Нехай
задано дві площини
![]() і
і
![]() відповідно рівняннями:
відповідно рівняннями:
![]()
![]()
Двогранний кут
між площинами вимірюється лінійним
кутом, який дорівнює куту між нормальними
векторами цих площин
![]() та
та
![]() .
Тоді
.
Тоді
![]()
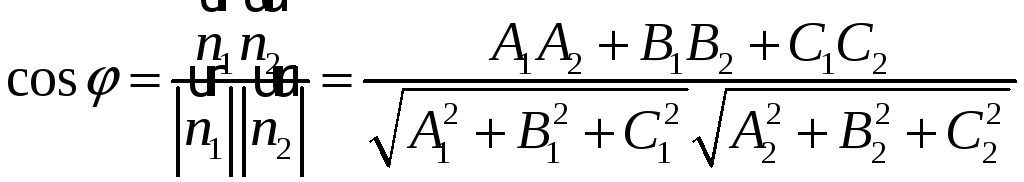 (5)
(5)
Якщо
![]() ,
то
,
то
![]() ,
а значить
,
а значить
![]() .
Тобто
.
Тобто
![]() (6) –умова
перпендикулярності площин.
(6) –умова
перпендикулярності площин.
Якщо
![]() ,
то
,
то
![]() ,
а значить їх координати пропорційні:
,
а значить їх координати пропорційні:
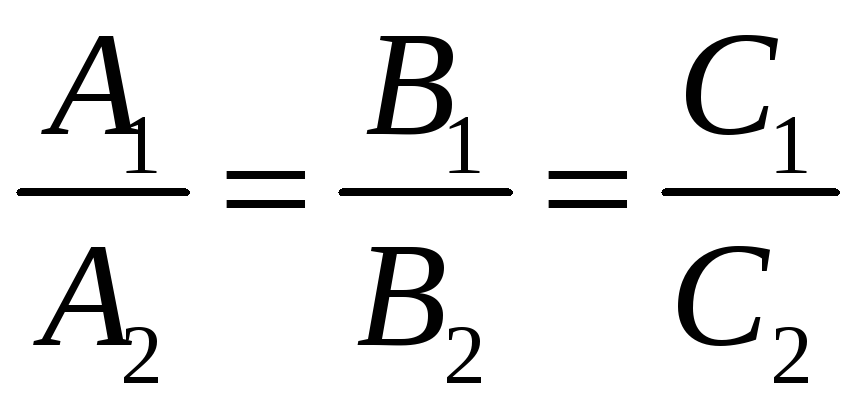 (7) –
умова
паралельності площин.
(7) –
умова
паралельності площин.
-
Відстань від точки до площини.
Якщо
площина
![]() задана
рівнянням
задана
рівнянням
![]() ,
а точка
,
а точка
![]() ,
то відстань від точки
,
то відстань від точки
![]() до площини
до площини
![]() обчислюють за формулою:
обчислюють за формулою:
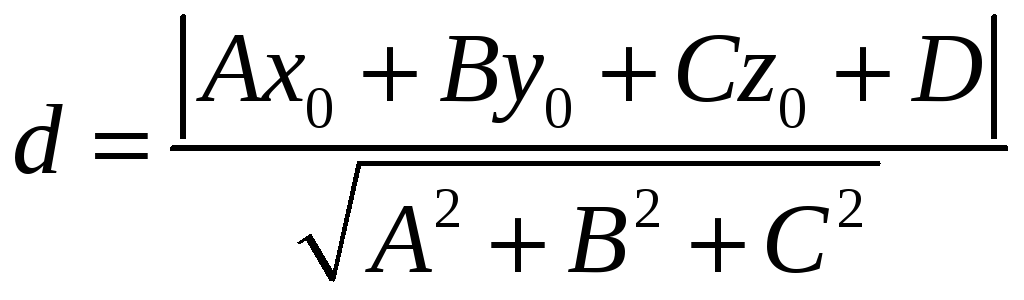 (8) –
відстань від точки до площини.
(8) –
відстань від точки до площини.
Приклад 3.
Знайти
висоту АН піраміди, заданої своїми
вершинами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Розв’язання:
За формулою (4) знаходимо рівняння площини, яка проходить через точки B, C, D.
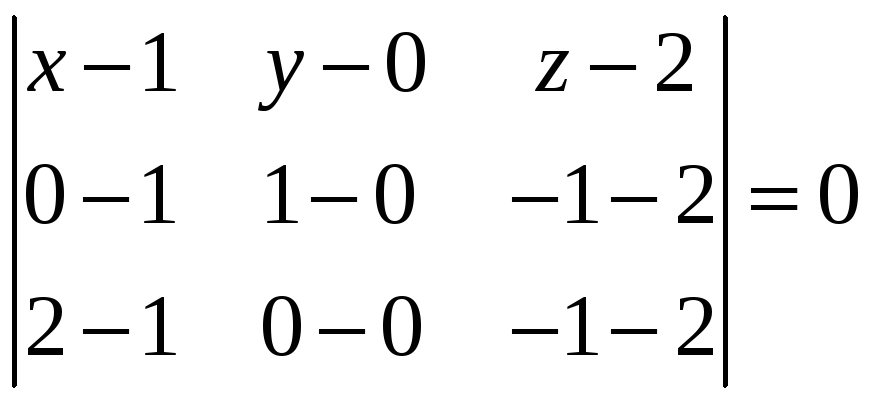 ,
,
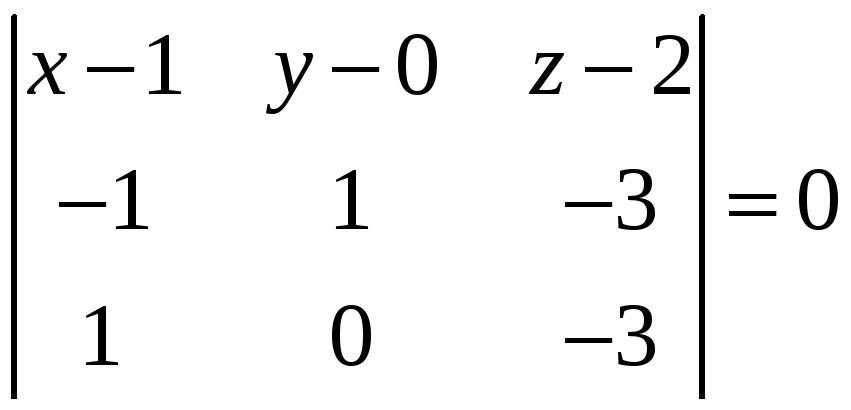 ,
,
![]() ,
,
![]() ,
,
![]() .
.
Висота
АН дорівнює відстані від площини BCD до
точки
![]() .
Тобто:
.
Тобто:
 .
.
-
К
 ут
між прямою і площиною. Умови паралельності
і перпендикулярності прямої і площини.
ут
між прямою і площиною. Умови паралельності
і перпендикулярності прямої і площини.
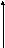

![]()


![]()


![]()
![]()


![]()





![]()
![]()





![]()
![]()




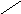

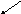
![]()
![]()
а) б)
Рис.1
Оскільки
![]() ,
то він утворює з направляючим вектором
,
то він утворює з направляючим вектором
![]() прямої
прямої
![]() кут
кут
![]() (коли
(коли
![]() рис. 1(а)) або
рис. 1(а)) або
![]() (коли
(коли
![]() рис. 1(б)).
рис. 1(б)).
Так як
під
![]() розуміють гострий додатний кут, то
розуміють гострий додатний кут, то
![]() ,
або
,
або
![]() .
Тобто
.
Тобто
![]() .
Одержимо:
.
Одержимо:
 (9) –
синус кута між прямою та площиною.
(9) –
синус кута між прямою та площиною.
5. Умови паралельності і перпендикулярності прямої і площини.
![]()
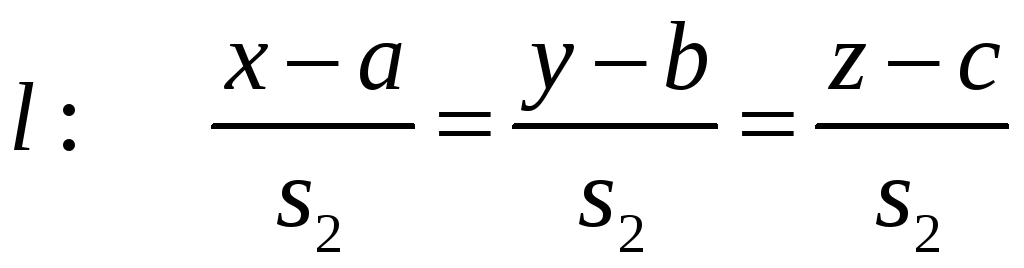 .
.
![]() ,
коли вектор нормалі
,
коли вектор нормалі
![]() площини
площини
![]() ,
напрямний вектор
,
напрямний вектор
![]() прямої
прямої
![]() перпендикулярні. Тобто
перпендикулярні. Тобто
![]() (10).
(10).
![]()
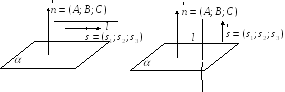 ,
при умові, що
,
при умові, що
![]() ,
тобто
,
тобто
 (11).
(11).
а) б)
Рис.2
Приклад 4.
Визначити
кут між прямою
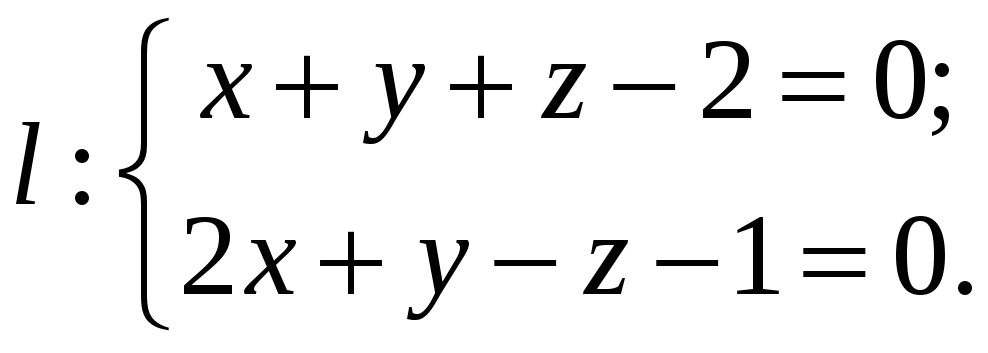 і площиною Р, яка проходить через
точки
і площиною Р, яка проходить через
точки
![]() ,
,
,
,
![]() ,
,
![]() .
.
