
- •Глава 5 исследование функций и построение графиков
- •5.1. Возрастание и убывание функций
- •5.2. Максимум и минимум функций
- •5.3. Наибольшее и наименьшее значения функции на отрезке
- •5.4. Выпуклость и вогнутость графика функции. Точки перегиба
- •5.5. Асимптоты графика функции
- •Вертикальные асимптоты
- •Горизонтальные асимптоты
- •Наклонные асимптоты
- •5.6. Общая схема исследования функции и построение графика
- •Упражнения
Глава 5 исследование функций и построение графиков
Одним из приложений производной является ее применение к исследованию функций, т.е. к характеристике поведения функции при изменении независимой переменной.
5.1. Возрастание и убывание функций
Согласно определению
(п.1.12), функция
![]() возрастает (убывает) на интервале
возрастает (убывает) на интервале![]() ,
если большему значению аргументах
из этого интервала соответствует большее
(меньшее) значение функции у.
,
если большему значению аргументах
из этого интервала соответствует большее
(меньшее) значение функции у.
Из определения
следует, что для возрастающей функции
приращение функции
![]() и приращение аргумента
и приращение аргумента![]() имеют одинаковые знаки, и следовательно,
их отношение положительно, т.е.
имеют одинаковые знаки, и следовательно,
их отношение положительно, т.е.
![]() .
.
Для убывающей
функции
![]() и
и![]() имеют противоположные знаки, в силу
чего, отношение приращений отрицательно:
имеют противоположные знаки, в силу
чего, отношение приращений отрицательно:
![]() .
.
Если функция в
интервале
![]() дифференцируема, то, переходя в
неравенствах к пределу при
дифференцируема, то, переходя в
неравенствах к пределу при![]() ,
получим:
,
получим:
− для возрастающей
в интервале
![]() функции
функции
![]() ;
;
− для убывающей
в интервале
![]() функции
функции
![]() .
.
Сформулируем необходимые и достаточные условия возрастания и убывания функции.
Теорема (необходимые условия).
Если дифференцируемая
на интервале
![]() функция
функция![]() возрастает (убывает), то ее производная
возрастает (убывает), то ее производная![]() неотрицательна:
неотрицательна:![]() (неположительна:
(неположительна:![]() )
для всех
)
для всех![]() .
.
Геометрически эта
теорема означает, что касательные к
графику возрастающей функции образуют
острые углы (![]() )
с положительным направлением осиОх
(рис. 5.1), а касательные к графику убывающей
функции − тупые углы (
)
с положительным направлением осиОх
(рис. 5.1), а касательные к графику убывающей
функции − тупые углы (![]() )
(рис. 5.2).
)
(рис. 5.2).
Теорема (достаточные условия).
Если функция
![]() дифференцируема на интервале
дифференцируема на интервале![]() и ее производная положительна:
и ее производная положительна:![]() (отрицательна:
(отрицательна:![]() )
для всех
)
для всех![]() ,
то эта функция возрастает (убывает) на
интервале
,
то эта функция возрастает (убывает) на
интервале![]() .
.

Рис. 5.1

Рис. 5.2
Таким образом,
изучение вопроса об участках возрастания
или убывания дифференцируемой функции
![]() сводится к исследованию знака первой
производной этой функции.
сводится к исследованию знака первой
производной этой функции.
Пример
Найти интервалы
возрастания и убывания функции:
![]() .
.
Функция определена на всей числовой оси.
Имеем
![]() ;
;![]() ;
;![]() .
.
Следовательно,
функция возрастает (« ↑ ») в интервале
![]() .
.
![]() ;
;
![]() .
.
Функция убывает
(« ↓ ») в интервале
![]() .
.
5.2. Максимум и минимум функций
Особую роль в исследовании функций играют значения х, отделяющие интервал возрастания от интервала убывания или наоборот.
Определение.
Точка
![]() называетсяточкой
максимума
(точкой
минимума)
функции
называетсяточкой
максимума
(точкой
минимума)
функции
![]() ,
если в некоторой окрестности точки
,
если в некоторой окрестности точки![]() выполняется неравенство
выполняется неравенство
![]()
![]() .
.
Значение функции в точке максимума (минимума) называют максимумом (минимумом) функции или экстремумом функции.
Из определения следует, что экстремум функции имеет локальный характер.
Рассмотрим условия существования экстремума функции.
Теорема (необходимое условие экстремума).
Если дифференцируемая
функция
![]() имеет экстремум в точке
имеет экстремум в точке![]() ,
то ее производная в этой точке равна
нулю:
,
то ее производная в этой точке равна
нулю:
![]() .
.
Геометрически
условие означает, что в точке экстремума
дифференцируемой функции
![]() касательная к ее графику параллельна
осиОх
(рис. 5.3).
касательная к ее графику параллельна
осиОх
(рис. 5.3).
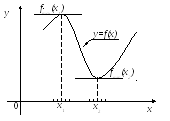
Рис. 5.3
Отметим, что
обратная теорема неверна, т.е., если
![]() ,
еще не означает, что
,
еще не означает, что![]() − точка экстремума. Например, для функции
− точка экстремума. Например, для функции![]() ее производная
ее производная![]() равна нулю при
равна нулю при![]() ,
но
,
но![]() не точка экстремума (рис. 5.4). Кроме того,
функция может иметь экстремум в точке,
в которой производная не существует.
Например, непрерывная функция
не точка экстремума (рис. 5.4). Кроме того,
функция может иметь экстремум в точке,
в которой производная не существует.
Например, непрерывная функция![]() производной в точке
производной в точке![]() не имеет, но точка
не имеет, но точка![]() − точка минимума
(рис. 5.5.).
− точка минимума
(рис. 5.5.).

Рис. 5.4 Рис. 5.5
Из этого следует, что непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.
Для того, чтобы выяснить в каких критических точках функция имеет экстремум устанавливают достаточные условия экстремума.
Теорема (первое достаточное условие экстремума).
Если непрерывная
функция
![]() дифференцируема в некоторой окрестности
критической точки
дифференцируема в некоторой окрестности
критической точки![]() и при переходе через нее (слева направо)
производная
и при переходе через нее (слева направо)
производная![]() меняет знак с плюса на минус, то
меняет знак с плюса на минус, то![]() есть точка максимума; с минуса на плюс,
то
есть точка максимума; с минуса на плюс,
то![]() − точка минимума.
− точка минимума.
Графическая иллюстрация теоремы приведена на рис.5.6.

Рис. 5.6
Замечание.
Если производная
![]() не меняет знака при переходе через
критическую точку, то функция в этой
точке не имеет экстремума (рис.5.7).
не меняет знака при переходе через
критическую точку, то функция в этой
точке не имеет экстремума (рис.5.7).
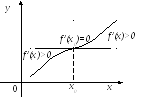
Рис. 5.7
Отыскания экстремумов функции обычно проводят по следующей схеме:
найти производную
 ;
;найти критические точки, в которых
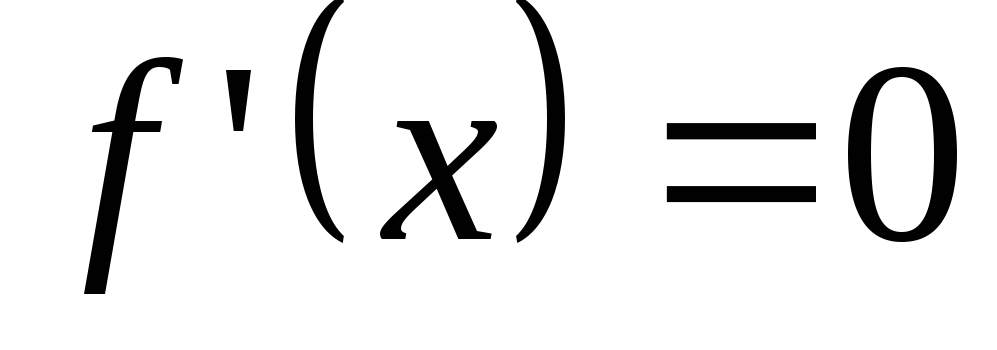 или
или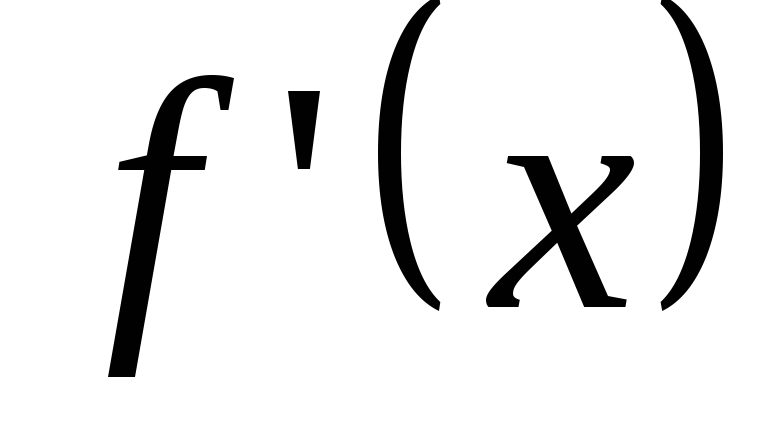 не существует;
не существует;исследовать знак
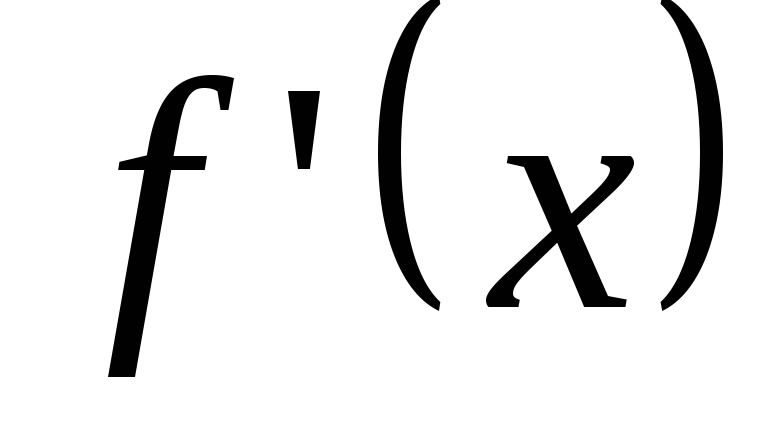 слева и справа от каждой критической
точки и определить экстремум (максимум
или минимум);
слева и справа от каждой критической
точки и определить экстремум (максимум
или минимум);вычислить значения функции в точках экстремума.
Пример
Найти экстремумы
функции:
![]() .
.
1)
![]() ;
;
2)
![]() ;
;![]() ;
;![]() ;
;
3)

![]() для
для
![]() ;
(« ↑ »);
;
(« ↑ »);
![]() для
для
![]() ;
(« ↓ »);
;
(« ↓ »);
![]() для
для
![]() ;
(« ↑ »);.
;
(« ↑ »);.
Значит,
![]() − точка максимума,
− точка максимума,![]() − точка минимума;
− точка минимума;
4)
![]() ;
;![]() .
.
Иногда, исследование
знака первой производной
![]() слева и справа от критической точки
вызывает затруднение. В этом случае
такое исследование можно заменить
определением знака второй производной
слева и справа от критической точки
вызывает затруднение. В этом случае
такое исследование можно заменить
определением знака второй производной![]() в самой точке. На этом основано второе
достаточное условие экстремума.
в самой точке. На этом основано второе
достаточное условие экстремума.
Теорема (второе достаточное условие экстремума)
Если в точке
![]() первая производная функции
первая производная функции![]() равна нулю:
равна нулю:![]() ,
а вторая производная в точке
,
а вторая производная в точке![]() существует и отлична от нуля:
существует и отлична от нуля:![]() ,
то при
,
то при![]() в точке
в точке![]() функция имеет максимум и минимум − при
функция имеет максимум и минимум − при![]() .
.
Пример
Найти экстремумы
функции:
![]() на отрезке
на отрезке![]() .
.
1)
![]() ;
;
2)
![]() ;
;![]() ;
;![]() ,
,![]() ;
;![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
![]() .
.
Значит,
![]() − точка минимума,
− точка минимума,![]() − точка максимума.
− точка максимума.
5)
![]() ;
;![]() .
.
Заметим, что второе
достаточное условие экстремума имеет
ограниченное применение по сравнению
с первым, поскольку неприменимо к точкам,
в которых производная не существует
или
![]() .
.
