ПБ 2-й курс набор 2012 г / заочники физика / ПБФизика / Лекции / Колебания

МЧС России

Санкт-Петербургский университет государственной противопожарной службы

Утверждаю

Начальник кафедры физики и теплотехники, полковник вн.сл. Иванов А.Н.

(должность, звание, ФИО)

«13» октября 2008 года

ЛЕКЦИЯ

по учебной дисциплине «Физика»

Специальность 280104.65 - Пожарная безопасность

Заочное отделение, 6 лет

Тема № 5 «Физика колебаний и волн »

Обсуждена на заседании кафедры

Протокол № 2/10 от

«13» октября 2008 года

Санкт- Петербург

2008

I. Цели занятия

1. Образовательная – изучение свойств и характеристик колебательного и волнового движения

2. воспитательные

- применение рассмотренных явлений и понятий в пожарной безопасности

- повышение квалификации сотрудников ГПС

II. Расчёт учебного времени

Содержание и порядок проведения занятия	Время, мин.
ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы: 1.Физика колебаний 2.Волны ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ	5 170 90 80 5

III. Литература

Основная:

1. Трофимова Т.И. Курс физики. - М.: Высшая школа, 2003, с.247-303.

Дополнительная:

Савельев И.В. Курс общей физики. - М.: Наука, 1989, Т.1.

Трубилко А.И., Звонов В.С., Поляков А.С., Дятченко А.А. Электричество. Пособие для самостоятельной работы - СПб.: СПбИПБ МВД России, 1998.

IV. Учебно-материальное обеспечение

1. Технические средства обучения: мультимедийный проектор, интерактивная доска.

V. Текст лекции

Вводная часть. Ставятся цели занятия.

Учебные вопросы

1 Физика колебаний

Незатухающий гармонический осциллятор. Познакомимся теперь с динамическим аспектом возникновения гармонических колебаний. Рассмотрим пример. Шарик массы под действием пружины совершает горизонтальное движение без трения (рис. 1). Каков характер движения шарика?

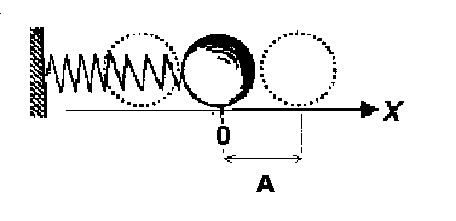
Рис. 1. Движение шарика под действием пружины

Если смещение шарика из положения равновесия достаточно мало, то сила, с которой деформированная пружина будут действовать на шарик, подчиняется закону упругих деформаций (Гука) . Напишем для шарика уравнение движения в форме второго закона Ньютона:

, (1)

,

где – смещение относительно положения равновесия, – положительный коэффициент, зависящий от упругих свойств пружины. Положим

, (2)

. (3)

Полученное нами линейное дифференциальное уравнение второго порядка (3) имеет общее решение :

, (4)

а , (5)

где произвольные постоянные и определяются начальными услови ями. Пусть в момент времени смещение , а скорость . Тогда, подставляя в (2.4) и (2.5), получим ; . Окончательно, общее решение уравнения (3) имеет вид:

. (6)

Это же решение может быть также записано как

. (7)

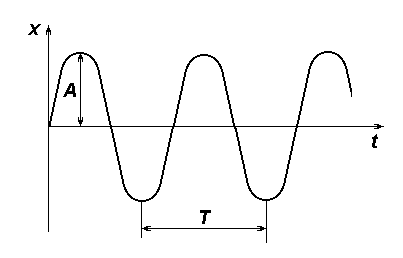
Рис. 2. График синусоиды

Механические колебания, возникающие под действием сил, развивающихся в самой колебательной системе, носят название собственных или свободных колебаний. Они возникают при всяком нарушении равновесия системы.

Амплитуда и фаза собственных колебаний определяются только начальными условиями. Циклическая частота не зависит от начальных условий и определяется свойствами самой системы. Физическая система, которая описывается дифференциальным уравнением вида (3), называется гармоническим осциллятором.

Электрический колебательный контур. Рассмотрим пример электрических колебаний. На схеме (рис.3) условно изображен контур, состоящий из последовательно соединенных емкости и индуктивности , но не обладающий электрическим сопротивлением. Отсутствие сопротивления – важнейшая из тех идеализаций, которые лежат в основе нашего изучения.

Разность потенциалов между обкладками конденсатора , где – заряд одной из обкладок, равна электродвижущей силе самоиндукции , возникающей в катушке, – сила тока в катушке:

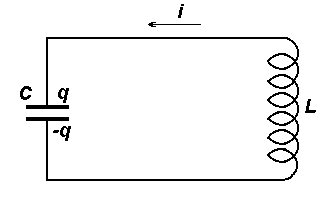
Рис. 3. Электрический колебательный контур

,

но сила тока связана с зарядом конденсатора соотношением:

.

Итак, дифференциальное уравнение колебаний заряда в контуре имеет вид:

.

Разделив на , получим:

или, положив ,

. (8)

Уравнение (8) имеет тот же вид, что и (3). Если конденсатор имеет начальный заряд или если в катушке возбужден начальный ток (например, в результате движения магнита около катушки), в контуре происходят электрические гармонические колебания:

.

Пусть – начальная величина заряда конденсатора и пусть в начальный момент времени сила тока равна нулю:

.

Имеем . Это дает , после чего решение принимает следующий окончательный вид:

.

Частота собственных электрических колебаний зависит от емкости и индуктивности . Для периода колебаний имеем:

.

Вывод. В гармоническом осцилляторе колебания возникают в результате действия двух факторов: восстанавливающей силы ( или или ), стремящейся вернуть систему в состояние равновесия (уничтожить деформацию пружины или отклонение маятника, разрядить конденсатор), и инерции (масса, индуктивность), благодаря которой система «проскакивает» положение равновесия и отклоняется в противоположную сторону  конденсатор перезаряжается, сжатая пружина превращается в растянутую.

Несмотря на то, что рассмотренные колебания имеют различную физическую природу (механические, электромагнитные и т. д.), возможен единый подход к их изучению, так как они описываются одними и теми же дифференциальными уравнениями.

Свободные затухающие колебания

Пренебрежение трением (электрическим сопротивлением) приводит к выводу о незатухающем характере колебаний. Однако из опыта известно, что при достаточно продолжительном наблюдении можно обнаружить постепенное уменьшение амплитуды колебаний вплоть до полного прекращения колебательного движения. Энергия движущегося тела при этом, в конце концов, переходит в тепло или, как говорят, диссипируется.

Пусть трение пропорционально скорости колебаний. Это утверждение представляет собой идеализацию реальных законов трения. Однако когда речь идет о жидком трении или трении о воздух при достаточно малых скоростях, это предположение находится в удовлетворительном соответствии с опытом. Итак, пусть сила трения для системы, совершающей одномерные колебания, равна:

, (9)

где – коэффициент трения, учитывающий все: вязкость среды, размеры движущегося тела и т. д. Добавим эту силу в правую часть уравнения движения (1):

. (10)

Разделим его на и введем обозначения:

,

.

где – частота собственных колебаний системы в отсутствие трения. Величина называется коэффициентом затухания и имеет размерность , также как и . Таким образом, имеем уравнение

. (11)

Пусть трение достаточно мало, так чтобы выполнялось условие:

.

Обозначим:

.

Уменьшение частоты при трении следовало ожидать заранее, так как трение вообще задерживает движение. Имеем:

. (12)

Уравнение (12) совпадает с (3). Его решение:

, (13)

где – амплитуда колебаний в начальный момент времени. Величина колеблется гармонически с периодом

.

Решение (11) в этих условиях можно записать как:

. (14) Эта функция является произведением убывающей показательной функции и синусоидальной функции . Описываемое ею движение представляет собой затухающие колебания (рис. 4а) Это движение можно рассматривать, как гармонические колебания с экспоненциально убывающей амплитудой , уменьшающейся от периода к периоду (рис. 4б).

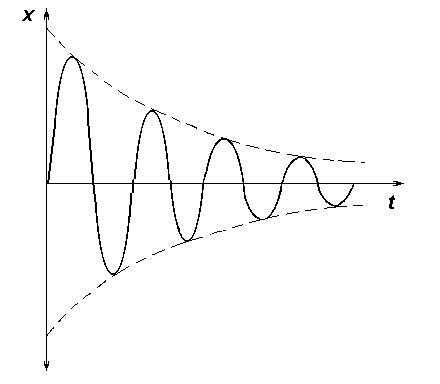
Рис. 4а. График затухающих колебаний

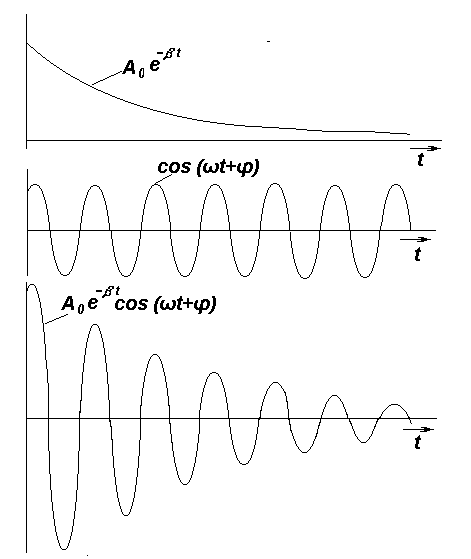
Рис. 4б. График затухающих колебаний

Строго говоря, (13) – уже отнюдь не гармоническое колебание; не является периодической функцией. Однако расстояние во времени между двумя последовательными прохождениями системы через положение равновесия (в одном и том же направлении) постоянно. Точно так же постоянно и равно той же самой величине расстояние во времени между двумя последовательными максимальными отклонениями. Этот промежуток времени мы будем называть условным периодом затухающего осцилляторного процесса.

Логарифмический декремент затухания. Натуральный логарифм отношения значений двух последовательных амплитуд колебаний называется логарифмическим декрементом затухания :

.

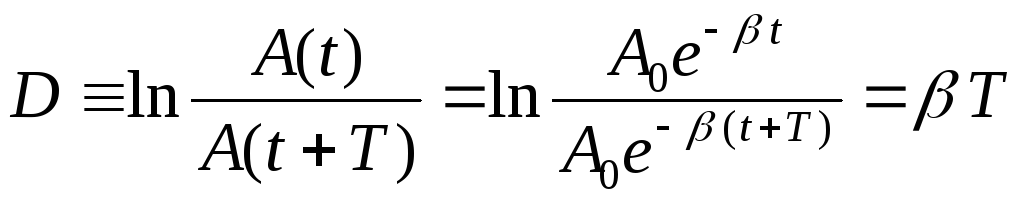Логарифмический декремент характеризует затухание колебаний за период, в то время как коэффициент затухания характеризует затухание колебаний за единицу времени. Физический смысл : обозначим через число колебаний, по прошествии которых амплитуда уменьшается в раз, а  промежуток времени, соответствующий этому уменьшению. Тогда:

и .

С другой стороны , но, по определению и

.

Таким образом, – есть величина, обратная числу колебаний, по истечении которых амплитуда спадает в раз. Пусть, например, . Это значит, что амплитуда колебаний уменьшается в раз по истечении 100 колебаний.

Вынужденные колебания осциллятора под действием синусоидальной силы

Если на тело действует колеблющаяся по величине внешняя сила, то тело будет совершать колебания, характер которых повторяет характер изменений внешней силы. Такие колебания называются вынужденными.

Пусть на осциллятор помимо упругой силы и силы трения действует еще и внешняя сила, зависимость которой от времени выражается формулой

(15)

где – круговая частота изменения внешней силы, вообще говоря, отличная от частоты собственных колебаний осциллятора, – амплитуда силы. Сейчас мы будем изучать картину установившихся под действием этой силы колебаний и не будем интересоваться переходным процессом, протекающим от момента включения (15) до установления регулярных колебаний.

Уравнение движения в форме второго закона Ньютона будет иметь такой вид:

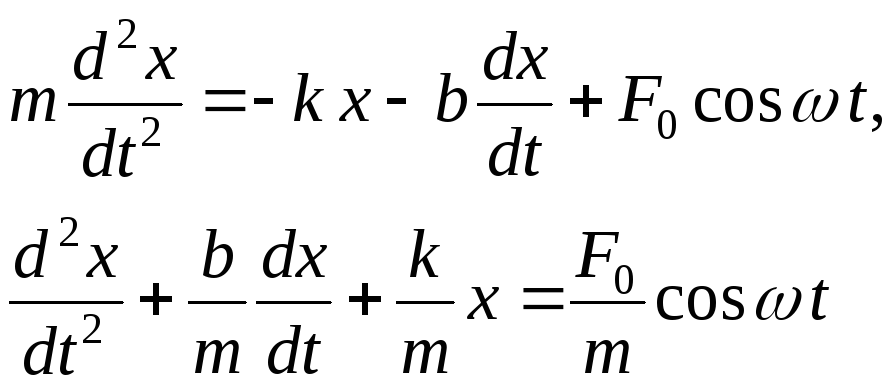₍₁₆₎

Введем привычные обозначения:

, и

и перепишем уравнение:

. (17)

Примечание: величина имеет смысл ускорения.

Интересующие нас установившиеся вынужденные колебания происходят по гармоническому закону с частотой, равной частоте внешней силы, т. е. по закону

. (18)

_Здесь

. (19)

Фазу найдем из второго уравнения системы (4.7):

. (20)

Анализ решения для амплитуды. Резонанс. Сначала выясним, как ведет себя амплитуда вынужденных колебаний при частотах внешнего воздействия близких и далеких от частоты собственных колебаний системы в случае, когда затухание колебаний мало, т. е. . Из (19) имеем:

а) при :

.

Амплитуда вынужденных колебаний равна величине статического смещения, которое вызвала бы постоянная по величине сила ;

б) при ;

в) при и ,

когда частота внешнего воздействия приближается к частоте собственных колебаний системы, величина уменьшается. При этом знаменатель (19) стремится к наименьшему значению, амплитуда возрастает и проходит через максимум при условии: , т. е. когда 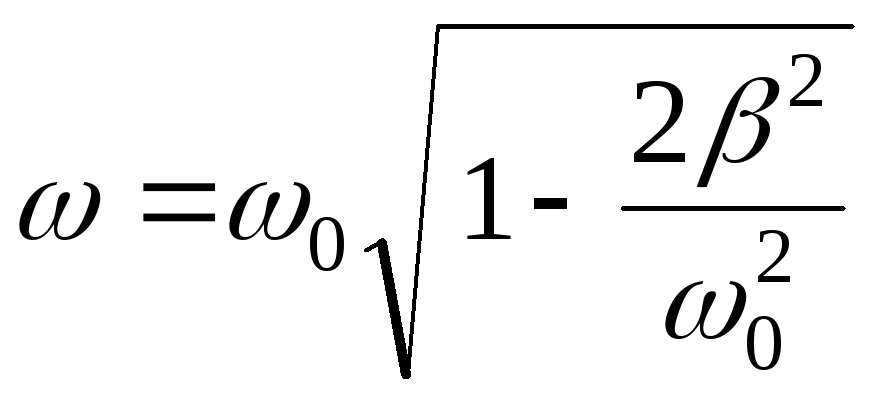, что при условии малости затухания сводится к приближенному равенству . В этом случае:

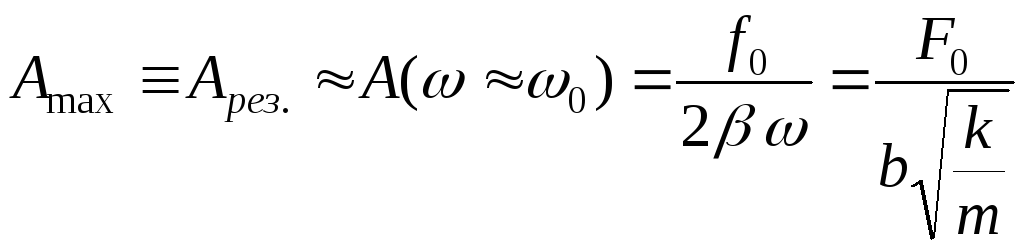
или, выражая через декремент затухания , откуда , имеем:

.

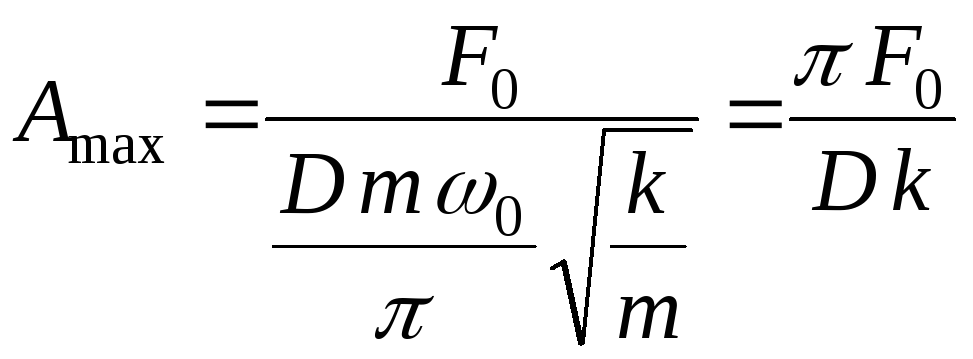График для амплитуды представлен на рис. 5.

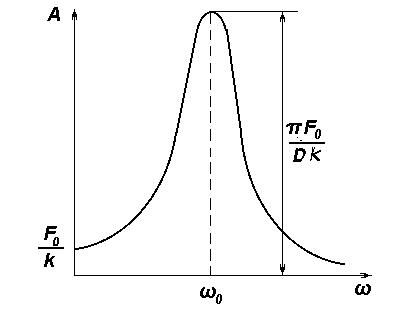
Рис. 5. Амплитудная резонансная кривая

Во сколько раз амплитуда в максимуме превосходит статическое (при ) значение? Имеем:

.

Отношение амплитуд определяется добротностью колебательной системы. Если добротность велика, то наибольшая амплитуда вынужденных колебаний во много раз превышает статическое отклонение.

Это резкое увеличение амплитуд вынужденных колебаний в области, где частота вынуждающей силы близка к частоте собственных колебаний системы , представляет собой наиболее характерную черту явления резонанса. Отметим, что во всех случаях , т. е. амплитуда вынужденных колебаний линейно зависит от амплитуды силы, вынуждающей колебания. Семейство кривых на рис. 6 соответствует разным значениям затухания. Это – амплитудные резонансные кривые.

Рис. 6. Семейство амплитудных резонансных кривых при различном затухании

2. Волны

Понятие волны. Как происходит распространение колебаний – передача воздействия от источника к приемнику. Как доходят до нашего уха колебания давления воздуха, возникающие около звучащего камертона? Каким образом свет, испускаемый звездами, достигает нашего глаза?

Для рассмотрения подобного рода вопросов необходимо ввести новое физическое понятие – волны. В физике волнами или волной называют всякое изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например плотности вещества, напряженности электрического поля, температуры.

Волной часто называют также всякое явление, при котором в пространстве происходит распространение кратковременного электрического или механического «толчка». Таким образом, понятие «волна» охватывает обширный круг явлений.

Замечание. Когда речь идет о волнах на поверхности воды, волной (в единственном числе) называют обычно совокупность одного горба и одной смежной с ним впадины. Когда говорят (также в единственном числе) «звуковая (или электромагнитная) волна такой-то частоты», всегда имеют в виду бесконечную вереницу «горбов» и «впадин».

Волновое уравнение. Рассмотрим произвольную функцию

(21)

от аргумента . Продифференцируем ее дважды по времени :

,

. (22)

Здесь штрих означает дифференцирование по аргументу . Теперь продифференцируем нашу функцию дважды по координате :

. (23)

Сравнивая (22) и (23), убеждаемся, что функция (21) удовлетворяет уравнению

или , (24)

в котором – фазовая скорость волны. Легко видеть, что этому же уравнению удовлетворяет произвольная функция аргумента :

(25)

а также сумма функций вида (21) и (25).

Дифференциальное уравнение в частных производных (24) называется волновым уравнением. При положительных значениях функции (21) и (25) изображают плоские волны, распространяющиеся, не деформируясь, со скоростью в сторону соответственно возрастающих или убывающих значений .

Плоская монохроматическая волна. Волновой вектор. Особый интерес представляет частный случай, когда функция синусоидальна:

. (26)

В каждой точке пространства, где значение фиксировано, величина совершает гармоническое колебание. Его амплитуда равна , а круговая частота равна . Обе эти величины одинаковы для всех . Фаза колебания равна . Она различна для различных и пропорциональна расстоянию от плоскости . Коэффициент пропорциональности между фазой и расстоянием называется волновым числом. При положительных значениях выражение (26) описывает волну, распространяющуюся в сторону возрастающих (слева направо), а выражение